Muito utilizado no mercado financeiro para estratégias long-short, arbitragem estatística, pairs trading e em análise e previsão de séries temporais macroeconômicas, o conceito de cointegração é ao mesmo tempo fascinante e intimidador de se compreender. Por isso, neste breve texto iremos explicar o que é cointegração com um exemplo intuitivo e fazer um exercício aplicado com pares de ações brasileiras usando o R!
Esse texto faz parte de uma série de publicações sobre séries temporais e pode ser melhor aproveitado se você ler o texto anterior sobre regressões espúrias (link aqui).
A analogia do bêbado e seu cachorro
As definições matemáticas de cointegração, e tópicos relacionados, são um tanto quanto sofisticadas, mas o seu conceito é simples o suficiente para ser introduzido com a cômica analogia do andar do bêbado e seu cachorro. Os créditos da analogia são inteiramente de Michael P. Murray que escreveu, em 1994, um paper didático de apenas 3 páginas elucidando o conceito de cointegração com o conto do andar do bêbado.
Imagine que você esteja andando na rua da sua cidade e aviste um bêbado que acaba de sair do bar, vagando em direção a sua casa. Você percebe que o bêbado caminha de maneira peculiar e imprevisível, algumas vezes se desviando para a esquerda e outras para a direita enquanto tenta, com dificuldades, seguir o seu caminho. Ao observar a trajetória do bêbado pode-se dizer que seus passos são nada mais do que uma sequência aleatória de passos. Na econometria, chamamos a trajetória do bêbado de passeio aleatório (random walk), de maneira a descrever o comportamento de muitas das séries econômicas que existem.
Por andar de forma aleatória, se você desviar o olhar e parar de observar o bêbado andando, será difícil dizer onde o bêbado estará após um determinado tempo, pois sua trajetória é imprevisível. Uma das características das trajetórias do tipo passeio aleatório, como a do bêbado, é de que a melhor previsão sobre um valor futuro é o último valor observado. Dessa forma, o seu palpite sobre a localização atual do bêbado poderia ser algo como o último lugar onde você o avistou, ou seja, na saída do bar.
Agora imagine que o bêbado tenha um cachorro amigo, sem coleira, que o acompanha. De forma similar ao bêbado, o cachorro também segue uma sequência aleatória de passos, sendo atraído por cada cheiro novo e estímulos que sente no caminho. Sempre que o bêbado percebe que o cachorro foi muito longe ele o chama: "Thor!". E o cachorro obedece o chamado retornando para perto de seu dono, caracterizando assim uma correção da distância entre ambos.
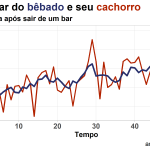
Se fossemos representar por meio de um gráfico a trajetória do bêbado e do cachorro ao longo do tempo e em relação a um ponto de referência qualquer (como o bar), seria algo como:
Observando as trajetórias de ambos, pode-se dizer que mesmo que a localização atual do bêbado após um tempo seja imprevisível, a localização do cachorro é relativamente previsível, pois ele não se afastará muito do seu dono. Dessa forma, agora um bom palpite sobre a localização do bêbado, por exemplo, pode ser dado uma vez que você tenha encontrado o cachorro, e vice-versa, pois conforme seguem dando passos aleatórios também corrigem a distância entre ambos. Na econometria, chamamos isso formalmente de mecanismo de correção de erros.
Note, também, que ambas as trajetórias são o que chamamos de séries temporais não-estacionárias, dado que quanto mais tempo passa é mais provável que o bêbado e seu cachorro estejam vagando bem longe de onde foram vistos por último. Se for verdade que a distância entre eles seja corrigida por um mecanismo de correção de erros, então a distância entre as trajetórias é dita cointegrada de ordem zero.
Para entender o que a expressão cointegrada de ordem zero significa, vale primeiro entender o que são séries integradas. Séries temporais não-estacionárias que se tornam estacionárias quando diferenciadas1 n vezes são ditas integradas de ordem n ou, simplesmente, I(n). Para duas séries temporais serem cointegradas, cada série precisa ser integrada de mesma ordem, n; por isso o termo cointegração. Sendo assim, um conjunto de séries temporais, todas integradas de ordem n, são ditas cointegradas se e somente se alguma combinação linear das séries é integrada de ordem menor do que n. Tal combinação linear foi chamada de relação de cointegração, conforme o trabalho de Engle e Granger (1987).
Cointegração no sentido de Engle-Granger
De maneira um pouco mais formal, partindo de um modelo de passeio aleatório para as trajetórias do bêbado (xt) e do cachorro (yt), temos:
ut = xt - xt-1
wt = yt - yt-1
onde ut e wt representam, respectivamente, o passeio aleatório do bêbado e do cachorro ao longo do tempo t e são ruído branco estacionários. Podemos então modelar a "trajetória cointegrada" do bêbado e do cachorro como:
ut + c(yt-1 - xt-1) = xt - xt-1
wt + d(xt-1 - yt-1) = yt - yt-1
onde ut e wt são novamente os passeios aleatórios do bêbado e do cachorro e os termos adicionais no lado esquerdo das equações são os termos de correção de erro pelo quais o bêbado e o cachorro corrigem a distância um do outro, ou seja, permanecem próximos. Podemos então dizer que, das equações acima, (yt-1 - xt-1) é uma relação de cointegração entre a trajetória do bêbado e do cachorro. Dessa forma, se estabelece uma relação de equilíbrio de longo prazo entre as trajetórias.
Note que se os termos de correção de erros forem não-estacionários, então as trajetórias modeladas para o bêbado e o cachorro também seriam não-estacionárias, portanto ambos iriam provavelmente se distanciar bastante ao longo do tempo. Nesse caso, diríamos que as séries temporais das trajetórias do bêbado e do cachorro não são cointegradas de ordem zero. No entanto, Engle e Granger (1987) provaram que se a trajetória do bêbado e do cachorro são ambas integradas de ordem 1 e seguem o descrito nas equações acima, então as trajetórias cointegram.
A analogia do bêbado e seu cachorro é uma boa forma de entender os conceitos básicos de cointegração e do mecanismo de correção de erro, no entanto, há inúmeros detalhes técnicos que devem ser considerados em aplicações com dados reais. Para se aprofundar mais no tema considere o curso de Séries Temporais da Análise Macro.
O conceito de cointegração é bastante utilizado em exercícios de macroeconomia, mas também pode ser usado no mercado financeiro com o objetivo de identificar relações — como a do bêbado e seu cachorro — entre ativos e realizar operações lucrativas com a técnica. Um exemplo disso são as estratégias de pairs trading, onde se realiza operações com pares de ativos que apresentem relação de cointegração de modo a obter lucro com a arbitragem. O grande desafio dessa aplicação é encontrar o par de ativo que apresente essas características.
Teste de Cointegração de Engle-Granger
De maneira prática, para verificar se um conjunto de séries temporais yt e xt cointegram, é preciso seguir os procedimentos propostos por Engle e Granger (1987):
- Verificar se as séries são estacionárias
- Estimar a regressão cointegrante das séries: yt = a + bxt + et
- Verificar se o resíduo da regressão cointegrante é estacionário usando os valores críticos de Engle e Granger (1987)
- Se o resíduo for estacionário, a regressão cointegrante não é espúria e pode-se estimar um modelo de correção de erros para obter a relação de equilíbrio das séries
A seguir mostraremos como aplicar o teste com um par de ações negociadas na B3 e para isso usaremos a linguagem R.
Exemplo no R
O exemplo utilizará o par de ações PETR3 e PETR4 no período de 28 de março de 2021 até 28 de março de 2022. Os dados são públicos e podem ser acessados pelo Yahoo Finance, havendo opção de usar pacotes ou web scraping para extrair os dados. O código abaixo faz a extração e tratamento de dados:
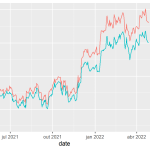
Antes de partir para o teste vale visualizar as séries temporais:
As séries parecem apresentar uma trajetória de passeio aleatório, como a do bêbado e seu cachorro, algo comum em séries de ativos financeiros.
Agora vamos para a primeira etada do teste de cointegração de Engle-Granger, ou seja, verificar se as séries são estacionárias. Podemos fazer isso com o teste ADF através da função adf.test():
Conforme os resultados, falhamos em rejeitar a hipótese nula do teste de a série ter raiz unitária, ou seja, as séries são não-estacionárias nos testes considerados (sem constante com tendência, com constante sem tendência e com constante e tendência).
Identificado que as séries são integradas de mesma ordem (nesse caso I(1), conforme pode ser confirmado usando a função forecast::ndiffs), podemos prosseguir com as etapas 2 e 3 que envolvem estimar a regressão cointegrante e verificar a estacionariedade do resíduo desta regressão. No R, isso tudo pode ser feito com a função coint.test(), que já toma o cuidado de usar os valores críticos corretos para testar os resíduos, conforme MacKinnon (1991).
Note que a função aplica 3 especificações: sem tendência, com tendência e com tendência ao quadrado. Em outros pacotes estatísticos e econométricos, como no Gretl, considera-se geralmente somente a primeira. Conforme os resultados, pelo p-valor da primeira especificação, sem tendência, temos que o resíduo da regressão cointegrante é estacionário. Em outras palavras, há evidências de que as séries PETR3 e PETR4 cointegram, para a amostra de dados selecionada.
Saiba mais
Para se aprofundar nos tópicos de cointegração, mecanismo de correção de erros e séries temporais de maneira geral, considere dar uma olhada no curso de Séries Temporais da Análise Macro.
Referências
Engle, R. F., & Granger, C. W. (1987). Co-integration and error correction: representation, estimation, and testing. Econometrica: journal of the Econometric Society, 251-276.
MacKinnon, J. G. (1991). Critical values for cointegration tests, Ch. 13 in Long-run Economic Relationships: Readings in Cointegration, eds. R. F. Engle and C. W. J. Granger, Oxford, Oxford University Press.
Murray, M. P. (1994). A drunk and her dog: an illustration of cointegration and error correction. The American Statistician, 48(1), 37-39.
1 Para entender mais sobre diferenciação veja este post.