Regressão espúria é quando tentamos relacionar variáveis que, por possuírem propriedades estatísticas semelhantes, apresentam correlação alta e significativa mesmo que não faça sentido. O cartum abaixo ilustra perfeitamente esse problema:
Note que a conclusão que o personagem do cartum chegou ao olhar um gráfico de linha dos dados não aparenta se sustentar se fizermos uma análise mais robusta, mesmo que para este caso nem seja necessário. Ou seja, apesar de os dados apresentarem uma propriedade estatística comum — de tendência de crescimento ao longo do tempo —, não há nada plausível que justifique a conclusão de que se todos rasparem a cabeça as vendas irão aumentar. Tal conclusão abriria espaço para outras interpretações ainda mais absurdas.
Exemplos de correlações espúrias como essa não faltam e acontecem rotineiramente, mas com menor frequência, até hoje. Uma rápida procura no Google, em meios de comunicação ou nas redes sociais é mais do que suficiente para encontrar algumas análises equivocadas. Existe até mesmo um site famoso (Spurious Correlations - Tyler Vigen) que compila diversos exemplos através de gráficos relacionando variáveis de séries temporais ao longo do tempo; e os resultados são impressionantemente bizarros, vale a pena dar uma olhada!
A regressão espúria é bastante comum em séries temporais, de modo que geralmente encontramos evidência estatística errônea de uma relação linear entre duas ou mais séries. Isso ocorre porque séries que apresentam tendência ao longo do tempo, por exemplo, são ditas não estacionárias, ou seja, são séries que vão crescer indefinidamente sem voltar ao seu valor médio. E essa característica de não estacionariedade pode levar a obtermos uma correlação significativa entre as séries somente por crescerem com o tempo, ou seja, não há necessariamente uma relação, mas ambas as séries crescem independentemente com a ação do tempo.
De maneira um pouco mais formal, teremos uma regressão espúria entre duas séries temporais quando:
- As séries Yt e Xt, independentes, são integradas de ordens diferentes;
- As séries Yt e Xt, independentes, são integradas de mesma ordem;
- Nesse caso, ou seja, com séries temporais não estacionárias, a regressão Yt = a +bXt + et é espúria.
Conforme o trabalho de Granger e Newbold (1974) — que já conta com mais de 10 mil citações —, através de simulações foi mostrado que regressões espúrias apresentam, em geral, algumas características:
- R2 alto
- Estatística Durbin Watson (DW) baixa
- Coeficientes significativos (alta chance de rejeitar H0: b = 0)
- Razão t não segue t de Student
- Estatística F não segue distribuição F
Consequências
Dessa forma, quando lidando com séries temporais não estacionárias devemos tomar muito cuidado, dado que:
- A econometria clássica não é válida quando as séries são não estacionárias;
- Em particular, se as séries não estacionárias forem independentes, obtém-se regressões espúrias;
- Diferenciar as séries até obter estacionariedade pode não resolver o problema, se o interesse é obter relações de longo prazo;
- Análise de cointegração pode ser uma solução.
De fato, a introdução do conceito de cointegração na literatura na década de 1980 levou os economistas Engle e Granger a ganharem o Prêmio Nobel de Economia de 2003.
Exemplo prático no R
Uma vez que você tenha entendido o que é uma regressão espúria de séries temporais, fica mais fácil observar esse fenômeno através de um exemplo prático.
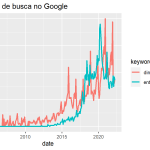
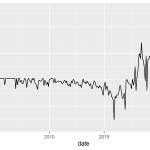
Utilizarei aqui dados reais disponíveis publicamente: serão duas séries temporais que medem o interesse das pessoas por termos de busca no Google, mais especificamente as procuras por "entrega ifood" e "dinossauro brinquedo" no Brasil obtidas no Google Trends. Esses termos são bem aleatórios, certo? A escolha foi intencional, com vistas a retratar que o problema de regressão espúria pode acontecer mesmo com duas séries que, a princípio, não possuem nenhuma relação, mas podem apresentar resultados estatisticamente significativos.
O código abaixo coleta, trata e gera uma visualização dos dados:
Note que as séries apresentam ser não estacionárias (tendência) e parecem, curiosamente, "caminhar juntas" ao longo do tempo. Podemos confirmar essa leitura calculando a correlação de Pearson entre as séries:
De fato, obtemos uma correlação alta para as séries, apesar de não fazer muito sentido.
Agora vamos regredir a série com o termo de busca "entrega ifood" contra a série do termo "dinossauro brinquedo" para verificar se encontramos uma relação linear significativa.
Que maravilha, não? Encontramos coeficiente bastante significativo, ao nível de 5%, e um R2 relativamente alto (0,63). O que isso significa? Apenas que encontramos uma regressão espúria, conforme pode ser confirmado pela estatística de Durbin-Watson abaixo, menor do que o R2:
Somente com essas informações já é suficiente para concluir que a regressão é espúria — mesmo que já soubéssemos disso desde o início pela própria escolha das variáveis —, mas você pode ir mais a fundo e verificar os resíduos da regressão. Em geral, nestes casos os resíduos serão não estacionários.
Saiba mais
Espero que o exercício tenha sido intuitivo o suficiente, sem pecar na formalidade, para entender sobre regressões espúrias e como identificá-las em modelos de séries temporais. Para se aprofundar no assunto confira os cursos de Análise de Séries Temporais e Econometria usando R e Python da Análise Macro.
Referências
Granger, C. W., & Newbold, P. (1974). Spurious regressions in econometrics. Journal of econometrics, 2(2), 111-120.