Usando Bagging e Bootstrap no R

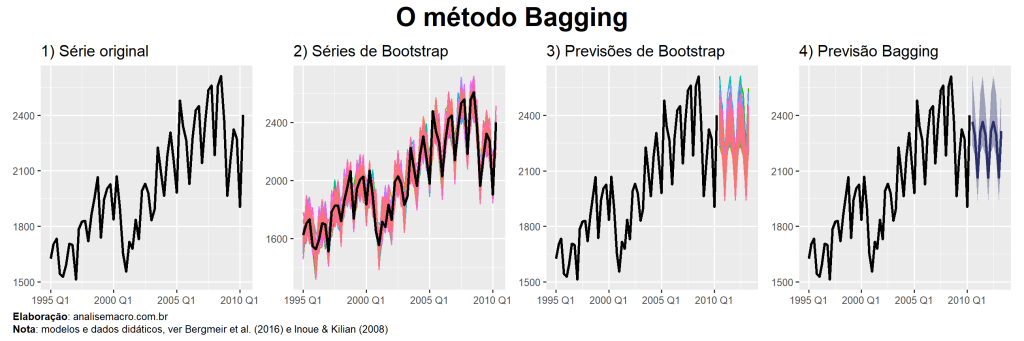
Bagging significa agregação de bootstrap e é um método estatístico que visa diminuir a instabilidade de modelos e reduzir o erro de previsão fora da amostra. A ideia é combinar previsões de vários modelos instáveis estimados para diferentes amostras de bootstrap, que é um processo de reamostragem aleatória com substituição. Normalmente, há muito mais a ganhar com combinações de modelos se forem muito diferentes e esse método procura explorar isso. Nesse texto mostramos como aplicar essa técnica proposta por Inoue & Kilian (2008) no R.

Principais características e vantagens do Bagging

Focando na utilização do Bagging para previsão de séries temporais a partir de modelos de regressão linear múltipla com regressores potencialmente correlacionados, os autores citados encontraram, entre outros resultados, que o método:

• É mais acurado em relação a grande parte dos métodos de previsão média/agregada ou modelos de fatores;
• Está par a par com outros métodos computacionalmente menos intensivos, como o estimador LASSO, Ridge regression e penalização Bayesiana;
• Pode ser usado quando os erros de regressão apresentam correlação serial e/ou heterocedasticidade (típico em séries econômicas/financeiras).

Os autores demonstram as vantagens do método usando, como exemplo, um problema de previsão para a inflação norte-americana (CPI), 1 a 12 meses à frente. Foram utilizadas 30 potenciais variáveis preditoras correlacionadas, retratando a atividade econômica do país em termos de produção, mercado de trabalho, variáveis monetárias e do mercado financeiro, além de dados do setor externo. O método foi aplicado e comparado com benchmarks tradicionais e métodos alternativos, através de validação cruzada, resultando em uma performance melhor ou similar em previsão fora da amostra para a maioria dos horizontes e modelos avaliados.

Como o Bagging funciona?

O algoritmo, em uma de suas variações, se inicia gerando um grande número de reamostragens de bootstrap com substituição, a partir das variáveis do problema de previsão. Em seguida, para cada um das amostras é estimado um modelo de regressão linear da variável de interesse (Y) contra as variáveis regressoras (X) aplicando uma regra de pré-seleção de coeficientes com base em um valor crítico da estatística t. Ou seja, o objetivo é "eliminar" coeficientes não significativos e essa é a chamada etapa de pré-seleção. A partir destes resultados, é estimado um novo modelo de regressão linear de Y contra as variáveis X pré-selecionadas, ainda usando as amostras de bootstrap. Por fim, os coeficientes dessas regressões são usados para previsão, onde se toma a média de todas as previsões (i.e. de cada previsão de cada amostra de bootstrap).

Em síntese, o algoritmo Bagging segue estas 4 etapas:

1. Para cada amostra de bootstrap, rode uma regressão MQO com todas as variáveis candidatas e selecione aquelas com uma estatística t absoluta acima de um certo limite c;
2. Estime uma nova regressão apenas com as variáveis selecionadas na etapa anterior;
3. Os coeficientes da segunda regressão são então usados para calcular as previsões na amostra real;
4. Repita as três primeiras etapas para B amostras de bootstrap e calcule a previsão final como a média das B previsões.

Conforme dito, mesmo que em termos de performance haja similaridade, o método apresenta variações. Para detalhes e uma melhor apresentação do Bagging veja Inoue & Kilian (2008).

Exemplo de implementação no R

Para implementar o método Bagging há algumas possibilidades: a família de pacotes {tidyverts}, apresentada neste post, oferece algumas facilidades, assim como o pacote {forecast} e outros. Neste exercício utilizarei o pacote {HDeconometrics}, também utilizado neste outro exercício.

Como exemplo, seguindo a provocação do texto no que se refere ao problema de previsão, defino como interesse a previsão da inflação brasileira, medida pelo IPCA (% a.m.). A fonte de dados utilizada será o dataset de Garcia et al. (2017), que traz uma série de variáveis referentes a índices de preços, variáveis macroeconômicas, de expectativas, etc., além da própria variável de interesse. O dataset compreende a janela amostral de janeiro/2003 a dezembro/2015, totalizando 156 observações e 92 variáveis.

Os dados e o código de exemplo são disponibilizados nos próprios exemplos de uso na documentação do {HDeconometrics}, sendo que apenas adapto para demonstrar com a finalidade de previsão. Se você tiver interesse em um exemplo com dados mais atualizados e em uma estratégia de previsão completa, confira o curso de Modelos Preditivos da Análise Macro.

O pacote {HDeconometrics} está disponível para instalação através do GitHub. Os comandos abaixo carregam o pacote e os dados para uso:

Em seguida realizamos a preparação dos dados, com vistas a estimar um modelo na forma do IPCA corrente contra defasagens das variáveis regressoras candidatas, definindo as últimas 24 observações como alvo de previsão:

Por fim, o modelo pode ser estimado com a função bagging() definindo o valor de R, que é o número de replicações de bootstrap que devem ser criadas, e o tipo de método de pré-seleção a ser utilizado, através do argumento pre.testing. Como exemplo, definimos 500 replicações e o uso de uma variação do procedimento exposto acima de pré-seleção (valor group-joint), conforme Inoue & Kilian (2008), onde a etapa é aplicada em grupos aleatórios de variáveis do conjunto de dados.

Opcionalmente, podem ser definidas variáveis como parâmetros fixos no modelo, através do argumento fixed.controls, além de outras parametrizações referente ao procedimento de reamostragem de bootstrap. Consulte a documentação e código correspondente para detalhes.

A seguir estimamos o modelo, calculamos as previsões 24 períodos a frente (pseudo fora da amostra) e plotamos o resultado comparando o valor observado do IPCA versus o previsto pelo modelo no período. Para procedimentos mais robustos de avaliação de modelos ver este texto ou os cursos da Análise Macro.

Apesar de ser um exemplo simples e sem muita robustez metodológica da forma como implementado, o resultado parece não ser ruim e, de fato, quando comparamos com outros modelos, o método Bagging se destaca em termos de acurácia de previsão do IPCA. Sinta-se livre para estimar outros modelos e realizar a comparação, assim como calcular o erro de previsão e métricas de acurácia.

Referências

Bergmeir, C., Hyndman, R. J., & Benítez, J. M. (2016). Bagging exponential smoothing methods using STL decomposition and Box-Cox transformation. International Journal of Forecasting, 32(2), 303–312.

Inoue, A., & Kilian, L. (2008). How Useful Is Bagging in Forecasting Economic Time Series? A Case Study of U.S. Consumer Price Inflation. Journal of the American Statistical Association, 103(482), 511–522.