Assumir distribuição normal para as variáveis, estimar modelos e produzir inferências ou previsões sem ao menos conhecer os dados e suas características antes é um problema tão comum em ciência de dados que já virou meme:
Em verdade, o conhecimento perfeito sobre a verdadeira distribuição dos dados é geralmente impossível. Isso ocorre porque normalmente observamos uma amostra de dados, que é um subconjunto de toda a população, e pode haver fatores não observados que afetam a distribuição da população. Ou seja, esse meme pode não fazer tanto sentido.
No entanto, em alguns casos, podemos ter uma boa compreensão do Processo Gerador dos Dados (DGP) e ser capazes de fazer suposições sobre a distribuição com base em fundamentos teóricos ou empíricos. Por exemplo, se estamos medindo a altura de seres humanos adultos, sabemos que a distribuição provavelmente será aproximadamente normal.
Além disso, em alguns casos, podemos fazer uso de técnicas estatísticas que são robustas a desvios da normalidade ou outras suposições sobre a distribuição. Por exemplo, algoritmos de aprendizado de máquina, como árvores de decisão e redes neurais, geralmente conseguem aprender relações complexas nos dados sem exigir suposições explícitas sobre a distribuição.
Mas o que seria esse processo que gera os dados? Por que é importante aprender sobre isso em ciência de dados? E como usar esse conhecimento de forma aplicada para entender e modelar os dados? Essas são questões relevantes para o profissional na área de dados e abordaremos elas de forma introdutória neste artigo, além de fornecer exemplos práticos usando linguagem de programação.
O que é o PGD?
Imagine que você tenha uma caixa com peças de Lego e um manual de instruções para montar um castelo. Se você não seguir as instruções, o seu castelo pode ficar incompleto ou esquisito. O manual de instruções é como se fosse o Processo Gerador dos Dados. Ele informa o que fazer com as peças para montar um castelo, assim como o PGD diz como diferentes variáveis se relacionam em um modelo e como elas criam os dados que observamos.
Essa analogia pode ajudar na compreensão, mas em termos mais formais o PGD é o processo ou mecanismo que gera os dados observados e usados na ciência de dados, com suas características e propriedades. Em outras palavras, é a maneira como os dados foram gerados ou criados, e é essencial entendê-lo para fazer inferências e previsões precisas e válidas a partir dos dados.
O processo de geração de dados pode variar dependendo do tipo de dados e do problema específico em estudo. Em alguns casos, os dados podem ser gerados por um processo físico, como medir a temperatura ou registrar o movimento. Em outros casos, os dados podem ser gerados pelo comportamento humano, como decisões de compra ou interações em redes sociais.
Para analisar os dados e tirar conclusões a partir deles, os cientistas de dados devem entender o processo de geração de dados e como ele afeta os dados. Esse entendimento pode ajudar a fazer suposições apropriadas, escolher modelos estatísticos apropriados e interpretar os resultados corretamente.
Como identificar o PGD?
Em geral, o processo que gera os dados é quase sempre desconhecido ou impossível de ser determinado com perfeição. Na prática fazemos suposições sobre os dados, assumindo uma distribuição de probabilidade. O sucesso ou a falha do trabalho na área de ciência de dados será, em grande parte, determinado pela aproximação da distribuição empírica dos dados em relação a teórica.
Para ajudar nessa tarefa, existem vários métodos que podem ser usados para tentar identificar a distribuição de uma variável:
- Histogramas: um dos métodos mais simples e comumente usados para visualizar a distribuição de uma variável é criar um histograma. Um histograma é um gráfico que mostra a frequência de diferentes valores ou faixas de valores da variável. Ao examinar a forma do histograma, é possível obter uma ideia da distribuição geral da variável.
- Boxplots: um boxplot é outra ferramenta útil para identificar a distribuição de uma variável. Ele mostra a mediana, quartis e outliers dos dados e pode ajudar a identificar assimetria e valores extremos.
- Gráficos Q-Q: um gráfico Q-Q é um método gráfico para comparar a distribuição de uma variável com uma distribuição conhecida. Ele plota os quantis da variável em relação aos quantis da distribuição teórica, como a distribuição normal. Se a variável seguir a distribuição teórica, os pontos passarão por uma linha reta.
- Testes estatísticos: existem vários testes estatísticos que podem ser usados para testar a normalidade ou outras distribuições de uma variável, como o teste de Kolmogorov-Smirnov, teste de Anderson-Darling ou teste de Shapiro-Wilk. Esses testes podem fornecer uma avaliação formal de se a variável segue ou não uma distribuição específica.
Em geral, uma combinação desses métodos pode ser usada para tentar identificar a distribuição de uma variável, e é importante escolher o método apropriado com base na natureza dos dados e na questão de pesquisa.
Abaixo mostramos um exemplo prático de uma variável gerada a partir de uma distribuição normal e a comparação gráfica da distribuição empírica com as distribuições teóricas, o que permite identificar a distribuição dos dados ao procurar por aquela que mais se aproxima:
R
Código
summary statistics
------
min: -2.840244 max: 3.082058
median: 0.006864292
mean: 0.003858193
estimated sd: 1.010247
estimated skewness: -0.001187105
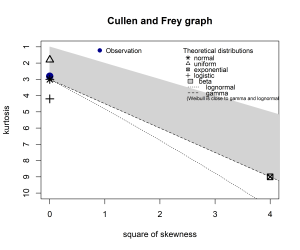
estimated kurtosis: 2.81323 A bola azul representa as estimativas dos valores de curtose e assimetria da variável simulada e as demais marcações no gráfico são distribuições teóricas. A distribuição teórica que mais se aproxima da distribuição observada é, provavelmente, a verdadeira distribuição e um bom palpite sobre o PGD.
Python
Código
{'model': {'name': 'lognorm', 'score': 0.005531390568385667, 'loc': -59.806532962730216, 'scale': 59.802147907155955, 'arg': (0.017147096378480997,), 'params': (0.017147096378480997, -59.806532962730216, 59.802147907155955), 'model': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000018C96D5CEB0>, 'bootstrap_score': 0, 'bootstrap_pass': None, 'color': '#e41a1c', 'CII_min_alpha': -1.66750856171884, 'CII_max_alpha': 1.7063137207986685}, 'summary': name score ... bootstrap_pass color
0 lognorm 0.005531 ... None #e41a1c
1 beta 0.005612 ... None #e41a1c
2 gamma 0.005636 ... None #377eb8
3 t 0.005825 ... None #4daf4a
4 norm 0.005825 ... None #984ea3
5 loggamma 0.006116 ... None #ff7f00
6 genextreme 0.007605 ... None #ffff33
7 dweibull 0.028522 ... None #a65628
8 uniform 0.583928 ... None #f781bf
9 expon 0.855852 ... None #999999
10 pareto 0.874242 ... None #999999
[11 rows x 10 columns], 'histdata': (array([0.00462499, 0.00924997, 0.01618745, 0.02543742, 0.05087484,
0.06012481, 0.08556223, 0.11099966, 0.12487461, 0.24049925,
0.29368659, 0.3214365 , 0.36999885, 0.36306137, 0.38387381,
0.36999885, 0.3538114 , 0.30987404, 0.28674911, 0.21274934,
0.18268693, 0.1294996 , 0.12256212, 0.05549983, 0.04856235,
0.02312493, 0.01156246, 0.00924997, 0.00231249, 0.00231249,
0.00693748]), array([-3.0735274 , -2.85556683, -2.63760626, -2.41964569, -2.20168511,
-1.98372454, -1.76576397, -1.54780339, -1.32984282, -1.11188225,
-0.89392168, -0.6759611 , -0.45800053, -0.24003996, -0.02207939,
0.19588119, 0.41384176, 0.63180233, 0.84976291, 1.06772348,
1.28568405, 1.50364462, 1.7216052 , 1.93956577, 2.15752634,
2.37548691, 2.59344749, 2.81140806, 3.02936863, 3.24732921,
3.46528978])), 'size': 1984, 'alpha': 0.05, 'stats': 'RSS', 'bins': 'auto', 'bound': 'both', 'name': 'popular', 'method': 'parametric', 'multtest': 'fdr_bh', 'n_perm': 10000, 'smooth': None, 'weighted': True, 'f': 1.5, 'n_boots': None, 'random_state': None}Código
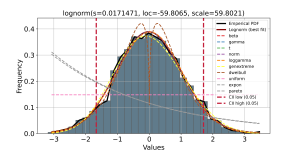
(<Figure size 1000x500 with 1 Axes>, <Axes: title={'center': '\nlognorm(s=0.0171471, loc=-59.8065, scale=59.8021)'}, xlabel='Values', ylabel='Frequency'>)Código
A linha preta representa a distribuição de probabilidade empírica da variável simulada e as demais linhas no gráfico são distribuições teóricas. A distribuição teórica que mais se aproxima da distribuição empírica é, provavelmente, a verdadeira distribuição e um bom palpite sobre o PGD.
Conclusão
Entender sobre a distribuição dos dados e o seu processo gerador (PGD) é fundamental para realizar previsões e inferências acuradas na ciência de dados. Nesse artigo trouxemos uma explicação didática sobre esses conceitos e um exemplo prático, usando linguagem de programação, para tentar identificar a distribuição de uma variável.
Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.