Previsão econômica com modelos ARIMA no Python

A família de modelos ARIMA constitui uma abordagem de previsão para séries temporais buscando descrever as autocorrelações dos dados, que é uma característica comum em dados econômicos. Esses modelos se popularizaram muito em 1970 com o trabalho de Box e Jenkins, que é a referência base sobre o assunto, e evoluíram para abordagens modernas de automatização com o trabalho de Hyndman e Khandakar em 2008, que contribuíram com a popularização de software open source para uso e aplicações destes modelos.

Existem muitos modelos ARIMA e aqui apresentaremos uma visão geral focando em 4 variações, nesta ordem:

Modelo AR
Modelo MA
Modelo ARIMA
Modelo SARIMA

O foco será desenvolver a intuição sobre os modelos para entender a mecânica de funcionamento, as representações em equações e a aplicação aos dados, com finalidade de previsão de séries temporais econômicas do Brasil. Exploraremos recursos visuais (gráficos) para facilitar a compreensão e demonstraremos aplicações dos modelos com exemplos práticos em Python.

A referência técnica utilizada é o livro-texto de previsão de séries temporais intitulado “Forecasting: Principles and Practice” de Hyndman e Athanasopoulos (2021).

Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.

Modelos auto-regressivos (AR)

Em regressão linear buscamos modelar a relação entre uma variável dependente $y_t$ e outras variáveis independentes $x_t$ , para prever $y_t$ usando uma combinação linear de $x_t$ . De forma similar, em modelos auto-regressivos (AR) estamos interessados em prever $y_t$ com base em uma combinação linear de valores passados de $y_t$ . Em outras palavras, o modelo AR é uma regressão da variável contra ela mesmo.

A intuição por trás desse modelo é que as observações passadas da série temporal possuem uma influência ou são preditoras dos valores futuros da série.

Por exemplo:

A taxa de juros Selic para o mês que vem será, provavelmente, um valor muito próximo ou igual ao valor do mês corrente.
A taxa de inflação, medida pelo IPCA, apresenta inércia (um termo do econômes que significa, de forma simplificada, o aumento dos preços correntes com base nos preços passados) devido a vários fatores, como a indexação de contratos de aluguel.

A forma comumente utilizada para representação desse modelo é:

$y_{t} = c + \phi_{1}y_{t-1} + \phi_{2}y_{t-2} + \dots + \phi_{p}y_{t-p} + \varepsilon_{t}$

onde:

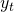$y_t$ é a série temporal alvo de previsão.
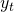$c$ é a constante ou intercepto do modelo, relacionado com a média de $y_t$ porém não é a média em si.
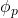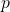$\phi_p$ é o $p$ coeficiente auto-regressivo a ser estimado, geralmente restrito em intervalos que geram modelos estacionários.
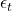$\epsilon_t$ é o termo de erro do modelo, um ruído branco.

É comum se referir a esse modelo usando o acrônimo AR(p), ou seja, um modelo auto-regressivo de ordem p, onde p é a ordem de defasagens no modelo.

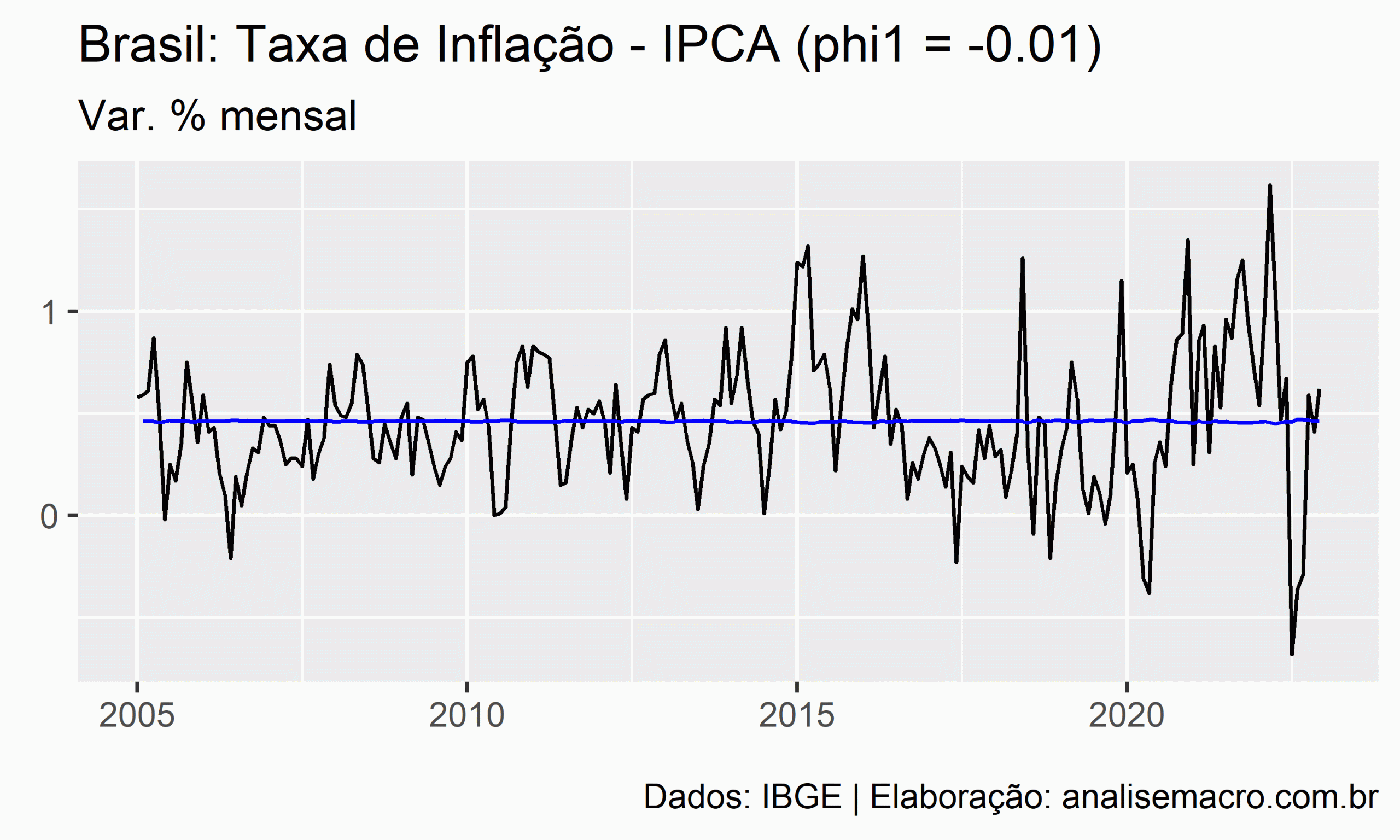
A ilustração abaixo mostra a linha de ajuste de um modelo AR(1) para diferentes valores de $\phi_1$ , no intervalo entre -1 e +1, usando como exemplo a série temporal da taxa de inflação medida pelo IPCA (IBGE):

A linha preta representa os dados observados e a linha azul representa o ajuste do modelo.

A estimação dos coeficientes $c$ , $\phi_1$ , $\dots$ , $\phi_p$ do modelo pode ser feita pela máxima verossimilhança (MLE), que é uma técnica para encontrar os valores para os coeficientes que maximizam a probabilidade de obter os dados que foram observados. A técnica é bastante similar à minimização da soma dos quadrados dos resíduos na regressão linear.

Exemplo de modelo AR(p) com código: taxa de inflação - IPCA

Agora vamos mostrar como utilizar o modelo AR(p) para previsão, usando como exemplo os dados exibidos acima da taxa de inflação medida pelo IPCA (IBGE). Abaixo reportamos (a) o sumário estatístico do modelo, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados com ajuste dentro da amostra e previsão fora da amostra.

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                  211
Model:               SARIMAX(1, 0, 0)   Log Likelihood                 -24.881
Date:                Mon, 05 Feb 2024   AIC                             55.763
Time:                        08:06:41   BIC                             65.818
Sample:                    01-01-2005   HQIC                            59.828
                         - 07-01-2022                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.1906      0.037      5.217      0.000       0.119       0.262
ar.L1          0.5864      0.052     11.185      0.000       0.484       0.689
sigma2         0.0740      0.005     14.893      0.000       0.064       0.084
===================================================================================
Ljung-Box (L1) (Q):                   0.02   Jarque-Bera (JB):                50.09
Prob(Q):                              0.90   Prob(JB):                         0.00
Heteroskedasticity (H):               4.20   Skew:                            -0.30
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.31
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
RMSE de treino: 0.2720257157158568
RMSE de teste: 0.2990384885047852

O código estima automaticamente a ordem p do modelo com base no menor critério de informação AICc. O modelo estimado é um AR(1):

$y_t = 0.1906 + 0.5864 y_{t-1} + \varepsilon_{t}$

onde $\varepsilon_t$ é um ruído branco com desvio padrão de $0.272= \sqrt{0.0740}$ . Note que as previsões geradas pelo modelo são relativamente boas pela simplicidade do modelo e captam, a olho nu, o retorno à média dos dados.

A linha preta no gráfico mostra os dados observados, enquanto que as linhas vermelha e azul mostram o ajuste dentro da amostra e a previsão fora da amostra, respectivamente.

Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Modelos de média móvel (MA)

Em modelos de média móvel (MA) busca-se prever os valores de uma série temporal $y_t$ com base em uma combinação linear de erros de previsão $\varepsilon_t$ passados de $y_t$ . Em outras palavras, é um modelo de regressão múltipla que usa os erros passados como variáveis independentes, em vez de outras variáveis observáveis.

A intuição por trás deste modelo é a suposição de que a variável $y_t$ reage a choques aleatórios com uma defasagem (delay), dessa forma, o choque defasado $\varepsilon_t$ é naturalmente uma variável a se colocar no modelo.

Por exemplo:

Imagine que o retorno diário de uma ação negociada na bolsa possa ser explicado por uma tendência e pelos efeitos ponderados de choques que aconteceram nos dias anteriores (acontecimentos políticos, desempenho econômico, decisões de investimento, etc.). É razoável supor que o choque do dia 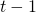$t-1$ terá um efeito importante no retorno da ação no dia 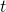$t$ , além de efeitos de choques que podem acontecer no próprio dia 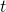$t$ . Extrapolando essa intuição, trata-se de um processo que pode ser modelado por um MA.

A forma comumente utilizada para representação desse modelo é:

$y_{t} = c + \varepsilon_t + \theta_{1}\varepsilon_{t-1} + \theta_{2}\varepsilon_{t-2} + \dots + \theta_{q}\varepsilon_{t-q}$

onde

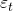$\varepsilon_t$ é o termo de erro do modelo (choque), um ruído branco.
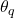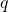$\theta_q$ é o $q$ coeficiente de média móvel a ser estimado, geralmente restrito em intervalos que geram modelos invertíveis.

É comum se referir a esse modelo usando o acrônimo MA(q), ou seja, um modelo de média móvel de ordem q, onde q é a ordem de defasagens no modelo.

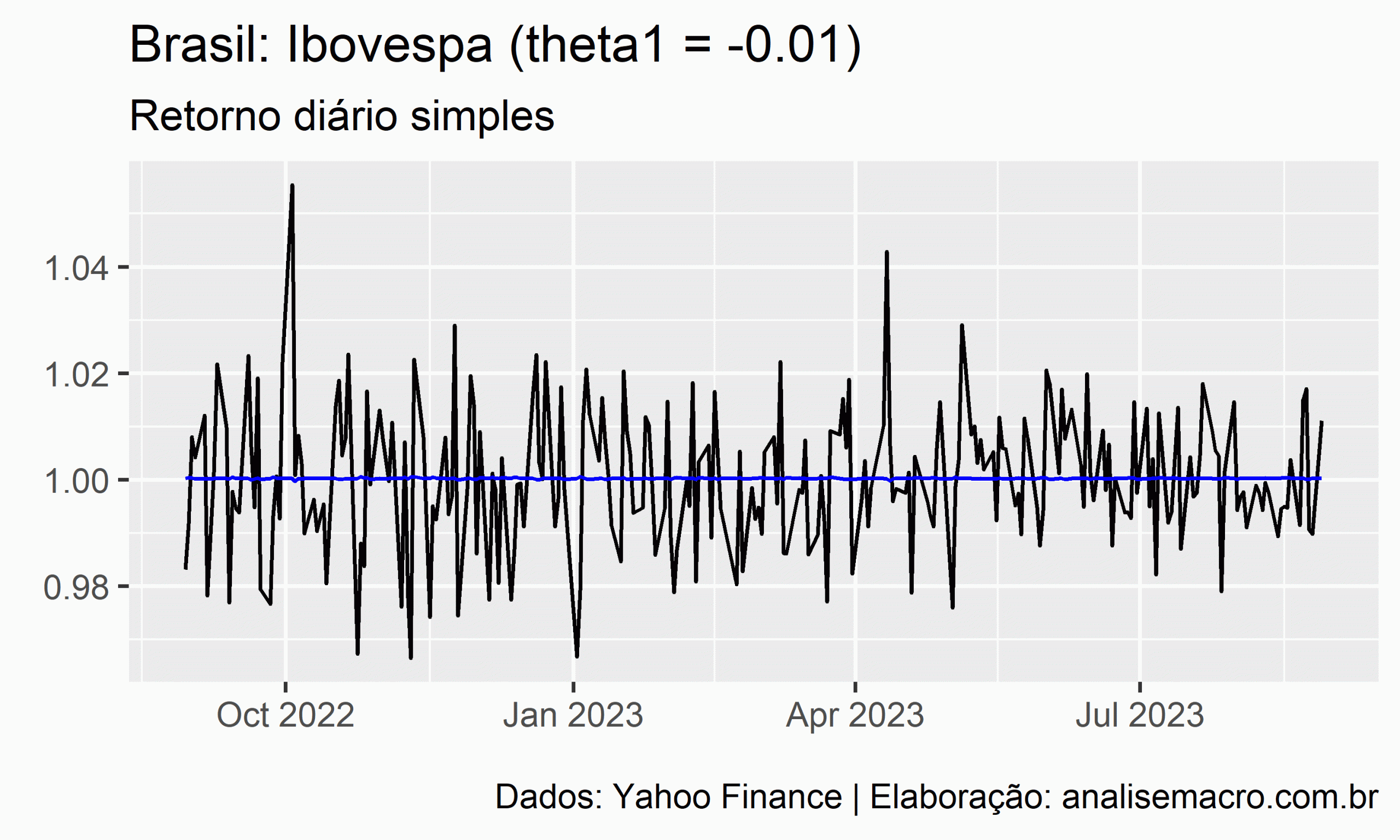
A ilustração abaixo mostra a linha de ajuste de um modelo MA(1) para diferentes valores de $\theta_1$ , no intervalo entre -0.99 e +0.99, usando como exemplo a série temporal dos retornos diários simples do Ibovespa (Yahoo Finance):

A linha preta representa os dados observados e a linha azul representa o ajuste do modelo.

A estimação dos coeficientes $c$ , $\theta_1$ , $\dots$ , $\theta_p$ do modelo pode ser feita pela máxima verossimilhança (MLE), que é uma técnica para encontrar os valores para os coeficientes que maximizam a probabilidade de obter os dados que foram observados. A técnica é bastante similar à minimização da soma dos quadrados dos resíduos na regressão linear.

Exemplo de modelo MA(q) com código: taxa de inflação - IPCA

Agora vamos mostrar como utilizar o modelo MA(q) para previsão, usando como exemplo os dados exibidos acima da taxa de inflação medida pelo IPCA (IBGE). Abaixo reportamos (a) o sumário estatístico do modelo, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados com ajuste dentro da amostra e previsão fora da amostra.

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                  211
Model:               SARIMAX(0, 0, 4)   Log Likelihood                 -21.730
Date:                Mon, 05 Feb 2024   AIC                             55.459
Time:                        08:08:39   BIC                             75.570
Sample:                    01-01-2005   HQIC                            63.588
                         - 07-01-2022                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.4596      0.046      9.952      0.000       0.369       0.550
ma.L1          0.5910      0.056     10.560      0.000       0.481       0.701
ma.L2          0.3337      0.068      4.872      0.000       0.199       0.468
ma.L3          0.3297      0.067      4.925      0.000       0.199       0.461
ma.L4          0.1147      0.063      1.812      0.070      -0.009       0.239
sigma2         0.0718      0.005     13.745      0.000       0.062       0.082
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):                37.19
Prob(Q):                              0.98   Prob(JB):                         0.00
Heteroskedasticity (H):               4.11   Skew:                            -0.13
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.04
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
RMSE de treino: 0.2679476899168494
RMSE de teste: 0.30324435848274084

O código estima automaticamente a ordem q do modelo com base no menor critério de informação AICc. O modelo estimado é um MA(4):

$y_t = 0.4596 + 0.5910 \varepsilon_{t-1} + 0.3337 \varepsilon_{t-2} + 0.3297 \varepsilon_{t-3} + 0.1147 \varepsilon_{t-4} + \varepsilon_{t}$

onde $\varepsilon_{t}$ é um ruído branco com desvio padrão de $0.268= \sqrt{0.07185}$ . Note que as previsões geradas pelo modelo são relativamente boas pela simplicidade do modelo, apesar de serem menos acuradas que o modelo AR(p) do exemplo acima, analisando pelo RMSE.

A linha preta no gráfico mostra os dados observados, enquanto que as linhas vermelha e azul mostram o ajuste dentro da amostra e a previsão fora da amostra, respectivamente.Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Modelos auto-regressivos integrados de média móvel (ARIMA)

Em modelos auto-regressivos integrados de média móvel (ARIMA) busca-se prever os valores de uma série temporal $y_t$ com base em uma combinação linear de valores de $y_t$ e de erros de previsão $\varepsilon_t$ , ambos defasados. Em outras palavras, é um modelo que combina diferenciação com os modelos auto-regressivo (AR) e de média móvel (MA).

A única novidade em relação aos modelos anteriores é o termo de integração (I), que é o contrário de diferenciação. O termo I é o número de diferenças necessárias para a série $y_t$ ser estacionária. A diferenciação é a mudança entre valores consecutivos de uma série temporal, podendo ser definida como:

$y'_t = y_t - y_{t-1}$

A estacionariedade é uma propriedade importante para esses modelos, significando que as características estatísticas (i.e., média, variância, etc.) de uma série temporal não dependem do tempo que elas foram observadas. Sendo assim, séries que apresentam tendência e sazonalidade, por exemplo, não são estacionárias.

A intuição por trás deste modelo é explorar as autocorrelações dos dados, ou seja, a relação entre valores defasados da série temporal. Partindo de uma série estacionária, esses modelos são úteis para quando as observações passadas da série temporal, assim como choques aleatórios defasados, possuem uma influência ou são preditoras dos valores futuros da série.

Por exemplo:

A taxa de inflação, medida pelo IPCA, apresenta inércia (um termo do econômes que significa, de forma simplificada, o aumento dos preços correntes com base nos preços passados) devido a vários fatores, como a indexação de contratos de aluguel, além de sofrer influência de choques de demanda ou oferta que podem acontecer na economia.

A forma comumente utilizada para representação desse modelo é:

$y'_{t} = c + \phi_{1}y'_{t-1} + \cdots + \phi_{p}y'_{t-p} + \theta_{1}\varepsilon_{t-1} + \cdots + \theta_{q}\varepsilon_{t-q} + \varepsilon_{t}$

onde $y'_t$ é a série temporal estacionária.

É comum se referir a esse modelo usando o acrônimo ARIMA(p,d,q), ou seja, um modelo auto-regressivo de ordem p, integrado de ordem d — onde d é o número de primeiras diferenças — e de média móvel de ordem q.

A estimação dos coeficientes $c$ , $\phi_1$ , $\dots$ , $\phi_p$ , $\theta_1$ , $\dots$ , $\theta_p$ do modelo pode ser feita pela máxima verossimilhança (MLE), que é uma técnica para encontrar os valores para os coeficientes que maximizam a probabilidade de obter os dados que foram observados. A técnica é bastante similar à minimização da soma dos quadrados dos resíduos na regressão linear. As mesmas restrições de coeficientes utilizadas nos modelos AR e MA também são aplicáveis aos modelos ARIMA.

A ilustração abaixo mostra o resultado de transformações de primeira diferença usando como exemplo a série temporal da taxa de câmbio BRL/USD (BCB):

A constante $c$ e a ordem $d$ possuem um efeito importante nas previsões de longo prazo deste modelo, em resumo:

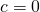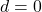Se $c=0$ e $d=0$ , a previsão de longo prazo tenderá para o zero.
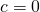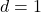Se $c=0$ e $d=1$ , a previsão de longo prazo tenderá para uma constante diferente de zero.
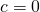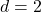Se $c=0$ e $d=2$ , a previsão de longo prazo tenderá para uma linha reta.
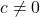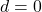Se $c\neq0$ e $d=0$ , a previsão de longo prazo tenderá para a média dos dados.
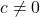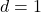Se $c\neq0$ e $d=1$ , a previsão de longo prazo tenderá para uma linha reta.
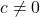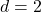Se $c\neq0$ e $d=2$ , a previsão de longo prazo tenderá para uma tendência quadrática.

Desta forma, se o objetivo da previsão é longo prazo, é importante verificar esses valores de um modelo ajustado para decisão de previsão fora da amostra.

**Exemplo de modelo ARIMA(p,d,q) com código: taxa de inflação - IPCA**

Agora vamos mostrar como utilizar o modelo ARIMA(p,d,q) para previsão, usando como exemplo os dados exibidos acima da taxa de inflação medida pelo IPCA (IBGE). Abaixo reportamos (a) o sumário estatístico do modelo, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados com ajuste dentro da amostra e previsão fora da amostra.

                               SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                  211
Model:               SARIMAX(1, 0, 0)   Log Likelihood                 -24.881
Date:                Mon, 05 Feb 2024   AIC                             55.763
Time:                        08:08:47   BIC                             65.818
Sample:                    01-01-2005   HQIC                            59.828
                         - 07-01-2022                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.1906      0.037      5.217      0.000       0.119       0.262
ar.L1          0.5864      0.052     11.185      0.000       0.484       0.689
sigma2         0.0740      0.005     14.893      0.000       0.064       0.084
===================================================================================
Ljung-Box (L1) (Q):                   0.02   Jarque-Bera (JB):                50.09
Prob(Q):                              0.90   Prob(JB):                         0.00
Heteroskedasticity (H):               4.20   Skew:                            -0.30
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.31
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
RMSE de treino: 0.2720257157158568
RMSE de teste: 0.2990384885047852

O código estima automaticamente as ordens p, d e q do modelo com base no menor critério de informação AICc. O modelo estimado é um ARIMA(1,0,0), que é o mesmo que um AR(1):

$y_t = 0.1906 + 0.5864 y_{t-1} + \varepsilon_{t}$

A linha preta no gráfico mostra os dados observados, enquanto que as linhas vermelha e azul mostram o ajuste dentro da amostra e a previsão fora da amostra, respectivamente.

Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Modelos sazonais auto-regressivos integrados de média móvel (SARIMA)

Em modelos sazonais auto-regressivos integrados de média móvel (SARIMA) busca-se prever os valores de uma série temporal $y_t$ com base em uma combinação linear de valores de $y_t$ e de erros de previsão $\varepsilon_t$ , ambos defasados e considerando a sazonalidade da série. Em outras palavras, é um modelo que adiciona termos sazonais para previsão da série temporal.

Agora o modelo é composto por componentes auto-regressivos, de integração e de média móvel sazonais, além das ordens de defasagem dos componentes não sazonais, ou seja:

$\text{ARIMA}\underbrace{(p, d, q)}_{\text{Não sazonal}}\underbrace{(P, D, Q)_{m}}_{\text{Sazonal}}$

sendo $_m$ a sazonalidade da série, a notação em caixa alta para componentes sazonais e em caixa baixa para componentes não sazonais.

A intuição por trás deste modelo é que as características sazonais dos dados possuem alguma influência para prever a série para o futuro. Assim as variações periódicas no tempo são utilizadas no modelo e esperadas no futuro.

Por exemplo:

O consumo de energia elétrica residencial no Brasil tem um pico no verão de cada ano, caracterizando uma variação sazonal.

Tomando como exemplo um ARIMA(1,1,1)(1,1,1)₄ sem constante, a forma comumente utilizada para representação desse modelo é:

$(1 - \phi_{1}L)~(1 - \Phi_{1}L^{4}) (1 - L) (1 - L^{4})y_{t} = (1 + \theta_{1}L)~ (1 + \Theta_{1}L^{4})\varepsilon_{t}$

onde:

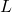$L$ é o operador de defasagem, ou seja, 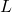$L$ operando em 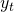$y_t$ tem o efeito de defasar a série em um período ( $L y_{t} = y_{t - 1}$ ).
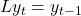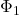$\Phi_1$ é o coeficiente auto-regressivo sazonal a ser estimado.
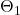$\Theta_1$ é o coeficiente de média móvel sazonal a ser estimado.

Os termos sazonais estão sendo multiplicados pelos termos não sazonais.

A estimação dos coeficientes $\phi_1$ , $\theta_1$ , $\Phi_1$ e $\Theta_1$ do modelo pode ser feita pela máxima verossimilhança (MLE), que é uma técnica para encontrar os valores para os coeficientes que maximizam a probabilidade de obter os dados que foram observados. A técnica é bastante similar à minimização da soma dos quadrados dos resíduos na regressão linear.

**Exemplo de modelo ARIMA(p,d,q)(P,D,Q)_m com código: taxa de inflação - IPCA**

Agora vamos mostrar como utilizar o modelo ARIMA(p,d,q)(P,D,Q)_m para previsão, usando como exemplo os dados exibidos acima da taxa de inflação medida pelo IPCA (IBGE). Abaixo reportamos (a) o sumário estatístico do modelo, (b) as métricas de acurácia de treino/teste e (c) o gráfico de valores observados com ajuste dentro da amostra e previsão fora da amostra.

                                      SARIMAX Results                                       
============================================================================================
Dep. Variable:                                    y   No. Observations:                  211
Model:             SARIMAX(1, 0, 0)x(0, 0, [1], 12)   Log Likelihood                 -23.280
Date:                              Mon, 05 Feb 2024   AIC                             54.560
Time:                                      08:08:56   BIC                             67.968
Sample:                                  01-01-2005   HQIC                            59.980
                                       - 07-01-2022                                         
Covariance Type:                                opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.1980      0.040      5.000      0.000       0.120       0.276
ar.L1          0.5716      0.056     10.142      0.000       0.461       0.682
ma.S.L12       0.1389      0.058      2.386      0.017       0.025       0.253
sigma2         0.0728      0.005     14.973      0.000       0.063       0.082
===================================================================================
Ljung-Box (L1) (Q):                   0.01   Jarque-Bera (JB):                73.21
Prob(Q):                              0.92   Prob(JB):                         0.00
Heteroskedasticity (H):               4.47   Skew:                            -0.34
Prob(H) (two-sided):                  0.00   Kurtosis:                         5.80
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
RMSE de treino: 0.2699351639065256
RMSE de teste: 0.27120676392452114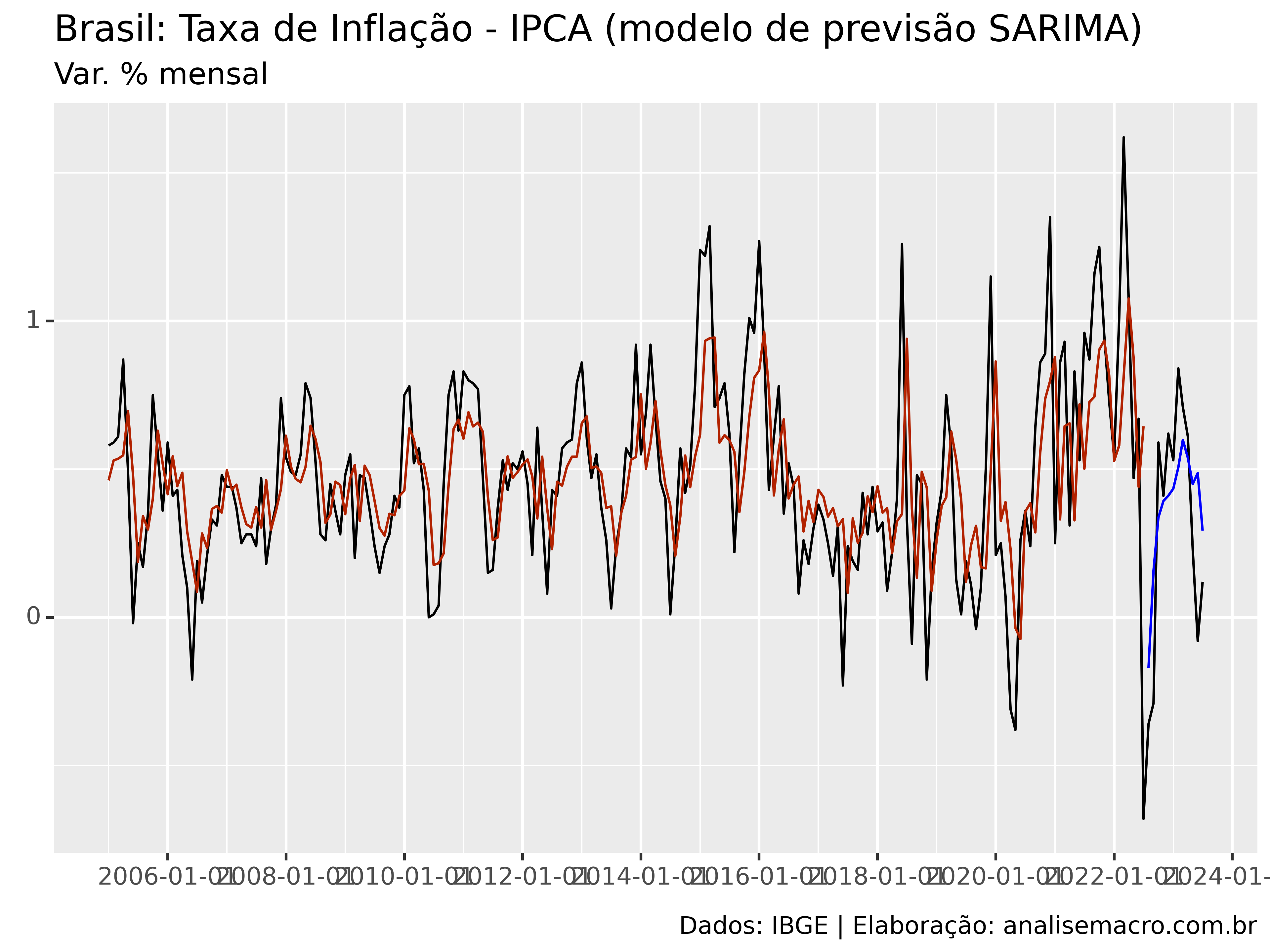

O código estima automaticamente as ordens p, d, q, P, D e Q do modelo com base no menor critério de informação AICc.

O modelo estimado é um ARIMA(1,0,0)(0,0,1)₁₂. Note que as previsões geradas pelo modelo são relativamente melhores em relação aos anteriormente expostos.

Conclusão

Neste texto abordamos modelos da família ARIMA para finalidade de previsão de séries temporais. Mostramos as diferenças de cada modelo com exemplos de dados econômicos do Brasil, em aplicações nas linguagens de programação R e Python.

Para uma metodologia de seleção das ordens de um modelo ARIMA(p,d,q) e mais informações técnicas veja Hyndman e Athanasopoulos (2021).

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Referências

Box, G. E. P., & Jenkins, G. M. (1970). Time series analysis: Forecasting and control. Holden-Day.

Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-08-29.

Hyndman, R. J., & Khandakar, Y. (2008). Automatic time series forecasting: The forecast package for R. Journal of Statistical Software, 27(1), 1–22. [DOI]

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise de impacto fiscal sobre o dolár com Python

Resultado IBC-br - Outubro/2024

Resultado PMC - Outubro/2024

Como usar Inteligência Artificial para Ler as Atas do COPOM?

Resultado PMS - Outubro/2024

Resultado IPCA - Novembro/2024

Outros artigos relacionados

Análise de impacto fiscal sobre o dolár com Python

Usamos uma cesta de 12 moedas para construir um cenário contrafactual da taxa de câmbio após o último anúncio de pacote fiscal, com base em modelagem Bayesiana. No período, o dolár depreciou quase 5% e passou os R$ 6,15, enquanto que na ausência da intervenção a moeda deveria estar cotada em R$ 5,78.

Resultado IBC-br - Outubro/2024

A Análise Macro apresenta os resultados da IBC-br de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PMC - Outubro/2024

A Análise Macro apresenta os resultados da PMC de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Previsão econômica com modelos ARIMA no Python

Modelos auto-regressivos (AR)

Exemplo de modelo AR(p) com código: taxa de inflação - IPCA

Modelos de média móvel (MA)

Exemplo de modelo MA(q) com código: taxa de inflação - IPCA

Modelos auto-regressivos integrados de média móvel (ARIMA)

Exemplo de modelo ARIMA(p,d,q) com código: taxa de inflação - IPCA

Modelos sazonais auto-regressivos integrados de média móvel (SARIMA)

Exemplo de modelo ARIMA(p,d,q)(P,D,Q)m com código: taxa de inflação - IPCA

Conclusão

Quer aprender mais?

Referências

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Outros artigos relacionados

Boletim AM

Boletim AM

**Exemplo de modelo ARIMA(p,d,q) com código: taxa de inflação - IPCA**

**Exemplo de modelo ARIMA(p,d,q)(P,D,Q)_m com código: taxa de inflação - IPCA**