Raio-X da inflação no Brasil usando o R: o papel da política monetária.

Ao longo das últimas semanas, o leitor foi exposto nesse espaço a uma série que tinha dois grandes objetivos. O primeiro, mostrar, de forma bem introdutória, como lidar com dados macroeconômicos na prática, usando o software R. O segundo, por sua vez, era entender o comportamento da taxa de variação dos preços no país, bem como gerar alguns modelos de previsão para a inflação, dados seus determinantes. Viu-se, de forma bastante detalhada, que a inflação alta está consolidada no país, não podendo ser associada a uma ou outra causa passageira. Se não é algo pontual, o que explica a inflação? Qual a sua causa básica? E o que a política monetária tem a ver com isso? É o que você verá nesse post.

Afinal, o que causa inflação?

Terminamos o último post dessa série nos perguntando o que havia em comum entre as tantas narrativas contadas no grupo de serviços. Havia no início da década de 80 do século passado algumas teorias no mercado para explicar a taxa de crescimento do nível geral de preços. Após a era Paul Volcker no Federal Reserve, entretanto, ficou combinado que a inflação era explicada pela diferença entre a taxa de crescimento dos meios de pagamento e do produto real de uma economia. Essa é a ideia por trás da teoria quantitativa, cujos primeiros rabiscos podem ser encontrados no ensaio Of Money, de 1752, escrito por ninguém menos que David Hume. Podemos ilustrar o argumento fazendo uso da equação de Cambridge, a partir do equilíbrio entre demanda

(1) $\begin{equation*} M^{d} = kPy \end{equation*}$

e oferta de moeda

(2) $\begin{equation*}M^{s} = M\end{equation*}$

Igualando (1) e (2) e reordenando os termos, chegamos à equação:

(3) $\begin{equation*}P = \frac{M}{ky}\end{equation*}$

Aplicando logaritmo e derivando em relação ao tempo, temos que:

(4) $\begin{equation*}\dot{P} = \dot{M} - \dot{k} - \dot{y}\end{equation*}$

Como $k$ é, por hipótese, constante, temos que:

(5) $\begin{equation*}\dot{P} = \dot{M} - \dot{y}\end{equation*}$

Em outros termos, a taxa de crescimento do nível geral de preços é dada pela diferença entre a taxa de crescimento dos meios de pagamento e do produto real da economia.

Essa teoria embasa a famosa frase do economista Milton Friedman, para quem "inflation is always and everywhere a monetary phenomenon". Ora, leitor, se a inflação é determinada positivamente pela taxa de crescimento dos meios de pagamento, fica claro que a condução frouxa da política monetária gera mais inflação. Ou, de outra forma, podemos relacionar a taxa de crescimento dos meios de pagamento à inflação através da taxa de juros. Isso foi proposto inicialmente por Knut Wicksell em sua obra Interest and Prices (1898), para quem a política monetária será expansionista se a taxa de juros de curto prazo estiver abaixo daquela considerada de equilíbrio entre oferta e demanda por fundos emprestáveis.

Nesse contexto, leitor, a causa da inflação ao longo do tempo deve ser buscada na condução da política monetária. Ao policymaker cabe calibrar a taxa básica de juros em torno daquela considerada de equilíbrio, natural ou neutra, de modo a manter a estabilidade de preços na economia. Foi essa a grande lição da Era Volcker à frente do Federal Reserve. Se é assim, para entender por que a inflação elevada está consolidada no país, como vimos ao longo dos posts dessa série, devemos olhar para a condução da política monetária brasileira.

Como o Banco Central brasileiro conduziu a política monetária nos últimos anos?

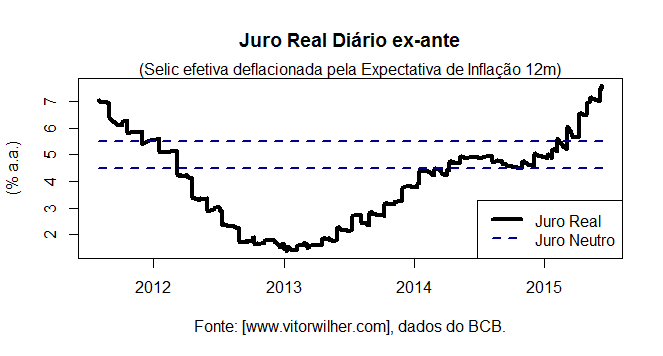
Em termos contemporâneos, inspirados no trabalho pioneiro de Knut Wicksell, dizemos que a política monetária é expansionista ou contracionista se, respectivamente, o juro real estiver abaixo ou acima da taxa de juros neutra (Blinder, 1999). Para verificar isso na prática, devemos primeiro definir o juro neutro. Para o presente exercício, vamos adotar a referência do paper 243/12, do FMI, que através de uma série de métodos chega a um intervalo de juro neutro no Brasil entre 4,5% e 5,5%. É razoável supor que no período recente, o juro neutro tenha oscilado ao redor dessa banda? Pode ser um pouco mais ou um pouco menos, mas como o leitor verá abaixo, isso perde importância diante da forte redução do juro real nos últimos anos.

Resolvido o problema do juro neutro, o nosso segundo desafio é definir o juro real. Pela equação de Fisher, sabemos que

(6) $\begin{equation*}i = r + \pi\end{equation*}$

Rearranjando os termos, definimos o juro real ex-post como:

(7) $\begin{equation*}r = i - \pi\end{equation*}$

Para tornar a análise ex-ante, devemos substituir $\pi$ pela expectativa de inflação, isto é, $\pi^{e}$ , de modo que o juro real ex-ante será dado por:

(8) $\begin{equation*}r = i - \pi^{e}\end{equation*}$

Em outras palavras, o juro real ex-ante será dado, de forma aproximada, pela diferença entre o juro nominal e a expectativa de inflação. Essa é, em geral, a forma como o mercado calcula a taxa de juros real no país.(*)

Dito isto, para estimar o juro real no Brasil, usamos a taxa Selic efetiva acumulada em 12 meses como proxy para a taxa nominal e as expectativas de inflação 12 meses à frente. Ambas disponíveis no site do Banco Central. No R importamos os dados, fazemos a conta acima e plotamos o juro real e a banda considerada neutra para o período de agosto de 2011 a junho de 2015.

O gráfico mostra que entre 1 de agosto de 2011 a 5 de junho de 2015, a taxa de juros real se manteve 65% do tempo abaixo de 4,5%, o limite mínimo da banda de neutralidade, aquela que não acelera a inflação. Ou seja, na maior parte desse período, o Banco Central brasileiro conduziu a política monetária de forma expansionista. E a inflação, leitor, como reagiu?

Juros real ex-ante granger causa inflação?

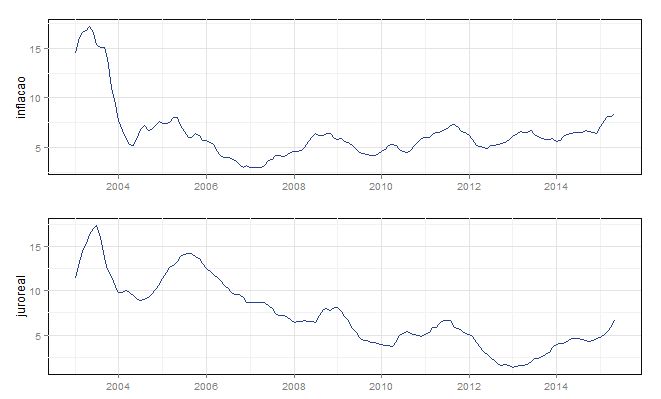
Mostramos que o que causa inflação é, em termos contemporâneos, a manutenção dos juros reais abaixo do juro neutro. Além disso, mostramos que o Banco Central brasileiro manteve os juros reais nos últimos anos abaixo do limite mínimo da zona neutra. Falta fazermos um exercício que mostra a relação entre inflação e juros reais. Para isso, pegaremos a média mensal da série de juro real que construímos acima e a inflação acumulada em 12 meses medida pelo IPCA, aquela que temos usado ao longo dessa série, para o período de janeiro de 2003 a maio de 2015. Um gráfico das séries, produzido com a função gtsplot é posto abaixo.(**)

Dá para ver que as séries não são estacionárias? Que tanto uma como a outra apresentam tendências? Caso não esteja claro para o leitor, é possível ver com a função stationarity do pacote BMR. Ou, claro, com outras funções, como as do pacote fUnitRoots ou do pacote urca. Feito isto, como as séries se relacionam ao longo do tempo? Podemos ver isso com a função lag2.plot do pacote astsa, que como já mostramos em um dos posts anteriores, verifica a relação entre as defasagens de uma série com a outra. Fizemos isso para as séries diferenciadas. Primeiro com o juro real defasado e depois com a inflação defasada.

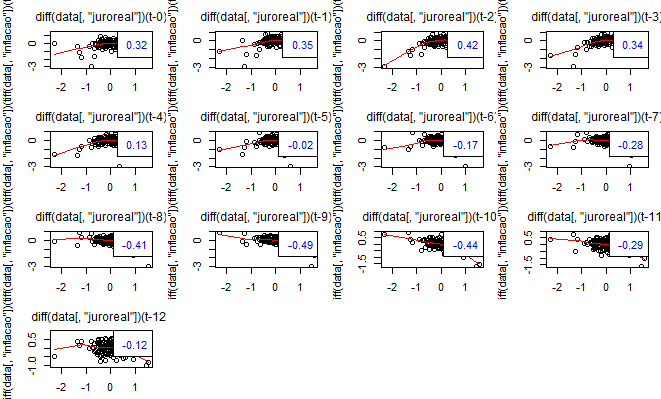
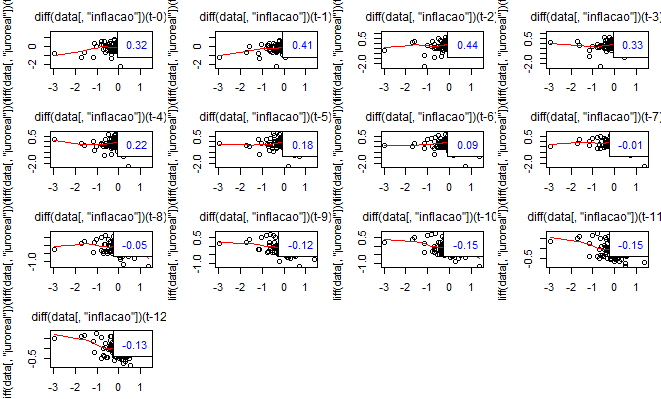
Observe que a correlação entre o juro real e a inflação é positiva até a quarta defasagem, sendo negativa a partir de então. Entre a inflação e o juro real o comportamento é similar: até a sexta defasagem há correlação positiva, sendo negativa da sétima em diante. Em outros termos, os resultados do exercício sugerem que apenas com o passar do tempo, a relação entre as duas variáveis passa a ser negativa. Isso parece ser estranho para o que estamos afirmando por aqui e, de fato, tem sido estudado pela literatura empírica como um puzzle, quando relacionado a mudanças na taxa de juros nominal e seus efeitos sobre a inflação.

Para avançarmos no entendimento da relação entre as variáveis, rodamos um teste de Granger, com as variáveis diferenciadas. O código é colocado abaixo. Para rodá-lo, você deve carregar o pacote vars.

######################### GRANGER CAUSALITY ##########################

VARselect(data,lag.max=12, type=c("const"),season=NULL)

grangertest(diff(data[,'juroreal'])~diff(data[,'inflacao']),
 order=9, data=data)

grangertest(diff(data[,'inflacao'])~diff(data[,'juroreal']),
 order=9, data=data)

Escolhemos nove defasagens para as equações e os resultados são postos abaixo.

> grangertest(diff(data[,'juroreal'])~diff(data[,'inflacao']),
+ order=9, data=data1)
Granger causality test

Model 1: diff(data[, "juroreal"]) ~ Lags(diff(data[, "juroreal"]), 1:9) + Lags(diff(data[, "inflacao"]), 1:9)
Model 2: diff(data[, "juroreal"]) ~ Lags(diff(data[, "juroreal"]), 1:9)
 Res.Df Df F Pr(>F)
1 120 
2 129 -9 1.3384 0.2243

> grangertest(diff(data[,'inflacao'])~diff(data[,'juroreal']),
+ order=9, data=data1)
Granger causality test

Model 1: diff(data[, "inflacao"]) ~ Lags(diff(data[, "inflacao"]), 1:9) + Lags(diff(data[, "juroreal"]), 1:9)
Model 2: diff(data[, "inflacao"]) ~ Lags(diff(data[, "inflacao"]), 1:9)
 Res.Df Df F Pr(>F) 
1 120 
2 129 -9 6.0479 5.664e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Em outros termos, para a hipótese nula juro real ex-ante não granger causa inflação há rejeição, enquanto para o caso contrário não. Movimentos na taxa de juro real ex-ante ajudam, desse modo, a explicar movimentos na inflação. Colhemos assim uma evidência empírica do que diz a teoria econômica: a condução da política monetária explica o comportamento da inflação ao longo do tempo.

E chegamos ao fim da série...

Mostramos ao longo de cinco posts que a inflação está alta no país e por que ela está alta. Fizemos isso mostrando 16 diferentes índices de inflação, abrindo o IPCA pelos seus 9 grupos e por suas classificações, além de demonstrarmos os conceitos de difusão e núcleos, bem como abrimos a inflação de serviços. Por fim, nesse post, mostramos que a causa da inflação é o descolamento entre as taxas de crescimento dos meios de pagamento e do produto real. Ou, em termos contemporâneos, pela manutenção dos juros reais abaixo da zona neutra, o que configura uma política monetária expansionista.

De fato, como o leitor pôde ver aqui, o Banco Central brasileiro reduziu a taxa de juros real a partir de agosto de 2011, levando a mesma para a mínima de 1,3% a.a. Isso contribuiu, de forma decisiva, para que a inflação experimentasse uma tendência de alta nos últimos anos. De modo a qualificar o argumento, fizemos um breve exercício com o teste de Granger, no qual vimos que taxa de juros real granger causa inflação, ou em outros termos, que mudanças na política monetária têm consequências sobre a inflação.

Em assim sendo, com esses cinco posts o leitor tem total condição de tanto entender por que a taxa de variação dos preços aumentou de forma contundente no país nos últimos anos, quanto ser introduzido ao mundo do R. Isso cobre, a propósito, 90% do que eu queria com a série Raio-X. E os outros 10%?

Pois é, os outros 10% eram gerar modelos de previsão da inflação. Ao longo das últimas semanas, entretanto, percebi que a construção de um curso de Análise de conjuntura usando o R não só era algo factível como tem bastante demanda entre estudantes de graduação e pós-graduação. Não apenas de economia, mas de outros cursos, como engenharia, contabilidade e administração, por exemplo. Desse modo, esse post encerra o módulo de inflação desse curso mais amplo que estou elaborando. Além dele, haverá módulos sobre nível de atividade, crédito e política monetária, política fiscal, economia internacional e setor externo, mercado de trabalho e, para terminar, previsão. Em outros termos, terminamos aqui o módulo de inflação da apostila e em outro post mais à frente, o leitor terá acesso a uma parte do módulo de previsão, com modelos baseados na Curva de Phillips e modelos ateóricos, que só se prestam a prever a inflação. Todos os outros módulos obedecerão ao mesmo procedimento. Espero que o leitor tenha gostado e continue apreciando os demais posts do blog. Abs

_______________________________________

Gostou do post? Quer aprender a fazer o mesmo? Dê uma olhada no nosso curso de Introdução ao R com aplicações em Análise de Conjuntura. Faça no Rio de Janeiro ou leve para sua empresa ou universidade!

____________________________________________________________________________________________

Notas:

(*) Em termos exatos, o cálculo se dá pela fórmula:

(9) $\begin{equation*}(1+r_{t+1}) = (1+i_t)/(1+E_t\pi_{t-1})\end{equation*}$

(**) Um exercício mais completo teria que envolver toda a "cadeia" por onde a decisão de juros passa até chegar aos preços. Para isso, é preciso ter em mente os canais de transmissão da política monetária. O leitor interessado pode saber mais sobre o assunto aqui e aqui.

____________________________________________________________________________________________

Blinder, A. S. (1999). Bancos Centrais: teoria e prática, São Paulo: Editora 34.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise exploratória para modelagem preditiva no Python

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Métodos de Reamostragem de Séries Temporais no Python

Coletando dados regionais do CAGED no Python

Coletando dados de Setores Censitários do Censo 2022 no Python

Estimando a inércia inflacionária através de modelos de espaço-estado usando Python

Outros artigos relacionados

Análise exploratória para modelagem preditiva no Python

Antes de desenvolver bons modelos preditivos é necessário organizar e conhecer muito bem os dados. Neste artigo, damos algumas dicas de recursos, como gráficos, análises e estatísticas, que podem ser usados para melhorar o entendimento sobre os dados usando Python.

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Prever séries temporais é uma tarefa frequente em diversas áreas, porém exige conhecimento e ferramentas específicas. Os modelos de machine learning do Sklearn são populadores, porém são difíceis de aplicar em estruturas temporais de dados. Neste sentido, introduzimos a biblioteca Skforecast, que integra os modelos do Sklearn e a previsão de séries temporais de forma simples.

Métodos de Reamostragem de Séries Temporais no Python

Nesta postagem, vamos mostrar alguns métodos simples para lidar com a reamostragem de dados de séries temporais no Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!