A Avenida Chile, no centro do Rio de Janeiro, sedia um prédio imponente: o Banco Nacional de Desenvolvimento Econômico e Social (BNDES), um dos maiores bancos estatais de fomento do planeta. Nos últimos dez anos, o BNDES foi protagonista de uma volta ao nacional desenvolvimentismo praticado no país nas décadas de 50 a 70 do século passado. A ideia dessa corrente de pensamento é que o Estado deve liderar uma estratégia de desenvolvimento, baseada na associação com empresas privadas estratégicas. Para o BNDES, em particular, coube a tarefa de ser o braço financeiro da operação, financiando a aquisição de máquinas e equipamentos, construção civil, fusões e aquisições. O objetivo era fazer a economia se desenvolver pela via do investimento. No quarto exercício do Códigos de Inverno 2016, o primeiro ebook do Clube do Código, queremos entender a relação entre os desembolsos do BNDES e a taxa de investimento da economia brasileira. A título de degustação, não membros do Clube podem baixar os arquivos e scripts desse exercício no repositório aberto da Análise Macro no GitHub. O endereço está ao final do exercício.
Coleta e tratamento de dados
Os dados que utilizaremos nesse exercício estão divididos em quatro blocos. O primeiro bloco vem do arquivo exercicio04.csv, que está disponível no repositório aberta da Análise Macro no GitHub. Ele contém duas séries trimestrais, com início em 1996T4, a saber: o Produto Interno Bruto (PIB) em valores correntes e a Formação Bruta de Capital Fixo (FBCF) em relação ao PIB. Importe para o R e transforme em série temporal com o código abaixo.
### Bloco 01 - PIB e FBCF bloco1 <- ts(read.csv(file='exercicio04.csv', header=T,sep=";",dec=","), start=c(1996,4), freq=4)
O segundo bloco vem do site do Banco Nacional de Desenvolvimento Econômico e Social (BNDES). Baixaremos a planilha de desembolsos mensais do Sistema BNDES por Setor CNAE com o código abaixo.
### Baixar planilha desembolsos mensais do Sistema BNDES por Setor CNAE
temp <- tempfile()
download.file('http://www.bndes.gov.br/SiteBNDES/export/sites/default/bndes_pt/Galerias/Arquivos/empresa/estatisticas/Int2_1D_m_setorCNAE.xls',
destfile=temp, mode='wb')
Uma vez baixada a planilha, carregue a mesma no R com a função loadWorkbook do pacote XLConnect e leia apenas a coluna 49, que se refere ao total de desembolsos com a função readWorksheet, como no código abaixo.
### Carregar e ler planilha bloco2 <- loadWorkbook(temp) bloco2 <- readWorksheet(bloco2, sheet = 1, header = TRUE, startRow = 5)[,49]
Um problema dessa planilha do BNDES é que ela é agrupada por anos, de modo que entre um ano e outro, há sempre um missing value e também o desembolso agregado. Nós devemos, portanto, retirar essas linhas, para então podermos transformar os dados em série temporal. O código abaixo faz isso.
### Retirar linhas com NA e valores anuais bloco2 <- bloco2[-c(13,14,27,28,41,42,55,56,69,70,83,84, 97,98,111,112,125,126,139,140,153,154, 167,168,181,182,195,196,209,210,223,224,228)] ### Transformar em série temporal bloco2 <- ts(bloco2, start=c(2000,1), freq=12) bndes <- bloco2
O terceiro bloco vem do Sistema Gerenciador de Séries Temporais do Banco Central. Importaremos para o R com o código abaixo as séries 4382, 2007 e 2043, referentes ao PIB mensal e ao estoque de crédito provido por instituições públicas e privadas, respectivamente. Ademais, também transformaremos os dados em séries temporais.
### Dados de entrada
series <- c(4382, 2007, 2043)
names <- c('PIB Mensal', 'CREDPUB', 'CREDPRIV')
start <- c(1996,10)
freq <- 12
inicio <- '01/10/1996'
fim <- '01/12/2015'
### Bloco 3 - PIB, Crédito Público e Privado
data <- getSeries(series, data.ini = inicio,
data.fim = fim)
### Organizar e transformar em série temporal
matrix <- matrix(NA, ncol=length(series), nrow=nrow(data)/length(series))
for(i in 1:length(series)){
matrix[,i] <- data$valor[data$serie==series[i]]
matrix <- ts(matrix, start=start, freq=freq)
colnames(matrix) <- names
bloco3 <- matrix
}
O quarto bloco é composto pelos créditos do Tesouro junto à instituições financeiras oficiais. Esse dado vem da planilha Dívida Líquida e Bruta do Governo Geral, disponível no site do Banco Central. Vamos pegar os dados que queremos com o código abaixo.
### Bloco 04 - Créditos do Tesouro junto à Instituições Oficiais
temp <- tempfile()
download.file("http://www.bcb.gov.br/ftp/notaecon/Divggnp.zip",temp)
divida <- unzip(temp, files='Divggnp.xls')
divida <- loadWorkbook(divida)
divida <- ts(t(readWorksheet(divida, sheet = "% PIB", header = TRUE,
colTypes = 'numeric')[40:41,-c(1:2)]),
start=c(2006,12), freq=12)*-1
colnames(divida) <- c('Híbrido', 'Crédito ao BNDES')
bloco4 <- divida
Uma vez importados esses quatro blocos, temos quatro objetos no R: bloco1, bloco2, bloco3 e bloco4. As séries que estão nos blocos 1 e 2 serão utilizadas no exercício entre os desembolsos do BNDES e a taxa de investimento, enquanto as séries dos blocos 3 e 4 serão para introduzir o exercício. Desse modo, para facilitar nossas incursões, vamos juntar os blocos 1 e 2.
Para fazer isso, um problema imediato é que os desembolsos do BNDES referem-se a dados mensais. No nosso exercício, nós vamos verificar a relação entre esses dados e a FBCF, logo precisamos tornar as séries comparáveis. Vamos, assim, acumular esses dados em termos anuais e depois vamos mudar a frequência, de mensal para trimestral, para podermos normalizá-los pelo PIB. Tudo isso é feito com o código abaixo.
### Anualizar dados do BNDES anual <- bloco2 anual <- (anual+lag(anual,-1)+lag(anual,-2)+lag(anual,-3)+ lag(anual,-4)+lag(anual,-5)+lag(anual,-6)+ lag(anual,-7)+lag(anual,-8)+lag(anual,-9)+ lag(anual,-10)+lag(anual,-11)) ### Trimestralizar desembolsos do BNDES bloco2 <- ts(aggregate(anual, nfrequency = 4, FUN=mean), start=c(2001,1), freq=4) ### Normalizar desembolsos pelo PIB bloco2 <- (bloco2/bloco1[,1])*100
Nesse contexto, podemos agora juntar a série de FBCF com os desembolsos do BNDES. Isso é feito no código abaixo.
data <- ts.intersect(bloco2, bloco1[,2])
colnames(data) <- c('BNDES', 'FBCF')
Temos, por suposto, o objeto data sobre o qual faremos nosso exercício. Para justificar a escolha desse tema, vamos utilizar os blocos 3 e 4 de dados. De modo a facilitar o entendimento, vamos normalizar o estoque de crédito pelo PIB com o código abaixo.
### Normalizar Crédito pelo PIB
credito <- (bloco3[,2:3]/bloco3[,1])*100
colnames(credito) <- c('CREDPUB', 'CREDPRIV')
Por fim, vamos renomear o bloco 4 como cgg, referente a créditos do governo geral com o código abaixo.
cgg <- bloco4
Pronto, leitor, agora podemos começar nosso exercício!
Exercício
A saída de Antonio Palocci do governo, no início de 2006, deflagrou uma série de mudanças na condução da política econômica. Em particular, houve o entendimento do Palácio do Planalto de que era preciso liderar medidas que fizessem a taxa de investimento da economia brasileira aumentar. Para tanto, os bancos públicos foram acionados com o objetivo de financiar a aquisição de máquinas e equipamentos, construção civil, fusões e aquisições.
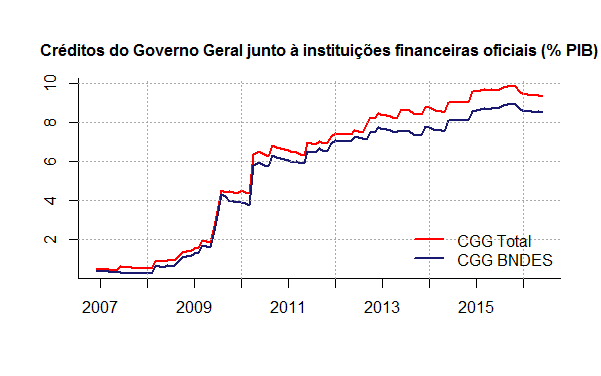
Para cumprir esse objetivo, o Tesouro passou a emitir títulos, sobretudo a partir de 2008, repassando os valores arrecadados para instituições financeiras oficiais. Em contrapartida, registrou-se na dívida bruta o valor repassado como crédito junto a essas instituições. A figura 16 ilustra a evolução desse montante. O BNDES, como pode ser visto, recebeu a maior parte desses recursos.
Há diversas consequências que podem ser vistas desse processo. Três, entretanto, se destacam, sendo duas imediatas. O estoque da dívida pública aumenta, bem como o fluxo de subsídios. Isto porque, o passivo do governo é remunerado por taxas mais elevadas do que o ativo junto àquelas instituições financeiras, implicando em um diferencial positivo que deve ser incorporado ao orçamento.
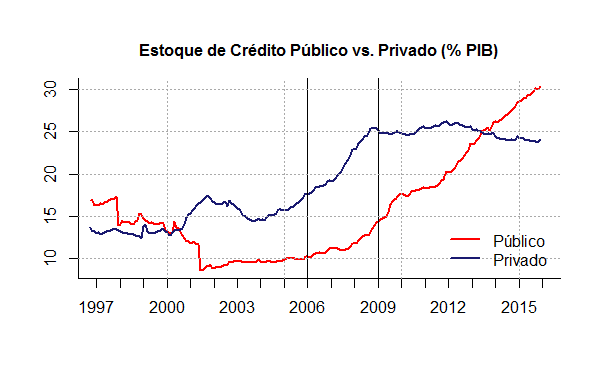
Uma outra consequência desse tipo de prática pode ser visto na figura 17. A capitalização dos bancos públicos fez com que aumentasse sua participação no estoque de crédito total. Com efeito, houve impacto na condução da política monetária. Isto porque, os empréstimos do BNDES e de outros bancos públicos são remunerados por taxas de juros menores do que as praticadas no mercado. Mudanças, portanto, da taxa de juros pelo Banco Central não tem efeitos sobre esses empréstimos. Sobre isso, ver o exercício A expansão do BNDES fez mal à economia brasileira: evidências da política monetária.
A figura 17 também mostra que a expansão do crédito público é anterior aos efeitos da crise financeira internacional, em sintonia com aquela mudança de política econômica em gestação no Palácio do Planalto. O plano era claro: liderar uma estratégia de desenvolvimento, baseada na associação com empresas privadas consideradas estratégicas. E o papel do BNDES era de protagonismo.
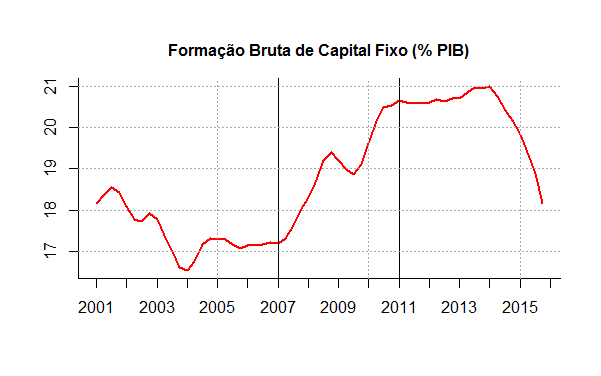
Dado o esforço de endividamento e coordenação feito pelo Palácio do Planalto, cabe perguntar se a estratégia deu certo. A figura 18 traz a evolução da Formação Bruta de Capital Fixo (FBCF) acumulada em quatro trimestres em relação ao PIB desde 2001. A série mostra um aumento entre 2007 e 2011, com estagnação e queda nos períodos seguintes.
Com efeito, se estamos interessados em avaliar a correção da estratégia do Planalto, um primeiro exercício que podemos fazer é verificar a relação dos empréstimos feitos pelos bancos públicos com a taxa de investimento. A ideia aqui é simples. Os desembolsos do BNDES, na medida que são financiados com recursos públicos, bem como implicam em custos não desprezíveis para a eficiência econômica, têm forte relação com a taxa de investimento? Em outras palavras, é possível dizer que o aumento nos desembolsos leva a aumentos significativos da taxa de investimento? Para iniciar nosso entendimento sobre essas e outras questões, precisamos primeiro entender como as duas séries se relacionam. É o que faremos na sequência do exercício.
Os desembolsos do BNDES
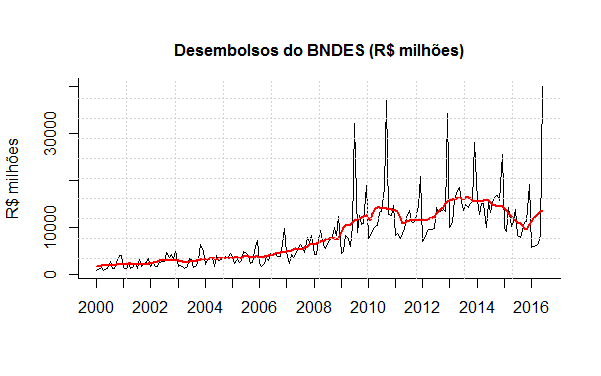
O BNDES, em um esforço de maior transparência, tem disponibilizado em seu site informações sobre os seus empréstimos. A figura 19 ilustra o comportamento dos desembolsos do banco desde janeiro de 2000 até dezembro do ano passado. O volume desembolsado pelo banco tinha média mensal de R$ 3,06 bilhões até 2006, passando para mais de R$ 11 bilhões a partir de 2007.
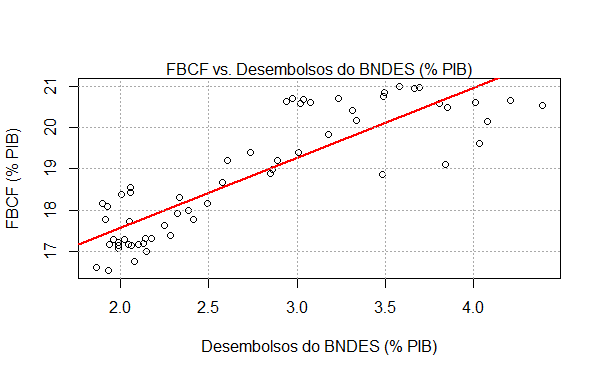
Feito o adequado tratamento dessa série de desembolsos, como visto na seção anterior, podemos nos perguntar sobre a relação dela com a taxa de investimento da economia brasileira. Um primeiro olhar sobre isso é feito na figura 20, quando plotamos a correlação entre as séries.
Como mostra o gráfico, as séries estão positivamente correlacionadas ao longo do tempo. Nesse contexto, vale perguntar se existe direção de causalidade entre elas, i.e., se os desembolsos do BNDES exercem influência na taxa de investimento ou vice-versa. Antes de fazer esse tipo de exercício, contudo, nós vamos investigar a estacionariedade da série.
Estacionariedade das séries
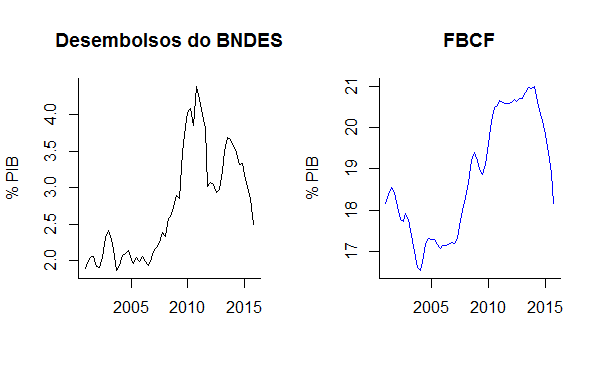
A figura abaixo coloca as séries de desembolsos do BNDES e FBCF lado a lado. São séries trimestrais, normalizadas pelo PIB, conforme visto na seção anterior. Para verificar se as séries são estacionárias, seguimos o protocolo contido em Pfaff (2008).
O procedimento para verificar raiz unitária pode ser visto no código do exercício, disponível no repositório aberta da Análise Macro no GitHub. Ao aplicá-lo, chega-se à conclusão que as séries são ambas integradas de ordem 1. Isso nos permite checar, portanto, se existe uma relação de cointegração entre as séries, antes de proceder um teste de causalidade. É o que fazemos a seguir.
Cointegração
Para verificar se as séries são cointegradas, vamos usar a metodologia contida em Johansen e Juselius (1992) e ilustrada por Pfaff (2008). No R, utilizamos a função ca.jo do pacote urca para implementar o procedimento de Johansen, como nos códigos abaixo. Aplicamos a função para o máximo autovalor e para o teste do traço.
jo.eigen <- ca.jo(data, type='eigen', K=6, ecdet='const', spec='transitory')
Pelo teste de máximo autovalor, é possível rejeitar ao nível de 5% a hipótese de que não há nenhum vetor de cointegração, bem como não se pode rejeitar a hipótese de o número de vetores de cointegração ser menor ou igual a 1. O mesmo, a propósito, pode ser visto no teste do traço. Em outros termos, há ao menos um vetor de cointegração entre a FBCF e os desembolsos do BNDES, de modo que podemos estimar um Vetor de Correção de Erros (VEC).
Vetor de Correção de Erros
Para estimar o VEC, vamos utilizar a função cajorls do pacote urca, como abaixo.
vec <- cajorls(jo.eigen, r=1)
Por fim, vamos transformar o VEC em um modelo VAR em nível com a função vec2var, como abaixo, para poder fazer uma análise de impulso-resposta e de decomposição de variância.
vec.level <- vec2var(jo.eigen, r=1)
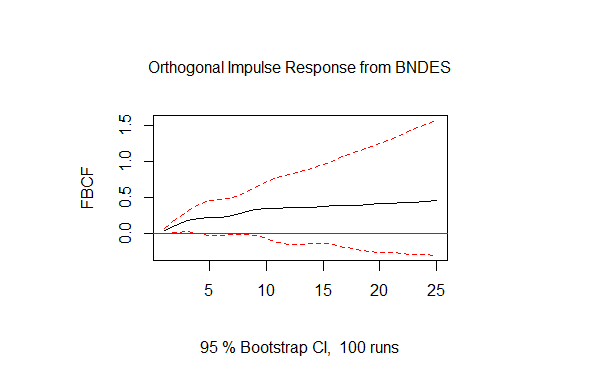
Feita a transformação, vamos fazer uma análise de impulso-resposta. Para isso, vamos usar a função irf do pacote vars. Primeiro, damos um impulso nos desembolsos do BNDES e vemos a resposta sobre a FBCF, depois fazemos o caso contrário.
irf.fbcf <- irf(vec.level, impulse='BNDES', response='FBCF', boot = T, n.ahead=24) plot(irf.fbcf) irf.bndes <- irf(vec.level, impulse='FBCF', response='BNDES', boot = T, n.ahead=24) plot(irf.bndes)
Como o leitor pode observar, tanto a FBCF reage a choques sobre os desembolsos do BNDES quanto o contrário também ocorre. Por fim, podemos fazer a decomposição de variância com a função fevd do pacote vars, como abaixo.
fevd(vec.level, n.ahead=12)
Os resultados da decomposição mostram que a variância dos desembolsos do BNDES é em grande parte explicada pela FBCF, passados 12 trimestres. Já a variância da FBCF mantém-se, no modelo estimado, explicada pela própria FBCF, mesmo passados 12 trimestres.
O procedimento de Toda-Yamamoto
A literatura econométrica tem citado comumente o procedimento contido em Toda e Yamamoto (1995) para o Teste de Causalidade de Granger em séries integradas de ordem maior ou igual a 1. Em linhas gerais, o procedimento consiste em realizar ajuste para que a estatística do teste de Wald siga a distribuição assintótica $\chi^2$. Os passos abaixo devem ser seguidos para realização do teste. Para outros detalhes sobre o teste, ver aqui e aqui.
\item Verificar a ordem de integração das variáveis através de testes de raiz unitária e estacionariedade;
\item Definir a ordem máxima (m) de integração entre as variáveis;
\item Montar o VAR em nível para as variáveis;
\item Determinar a ordem de defasagem do VAR(p) pelos critérios de informação tradicionais;
\item Ver a estabilidade do modelo, em particular problemas de autocorrelação;
\item Se estiver tudo certo, adicionar m defasagens ao VAR, de modo que você terá um VAR(p+m);
\item Rodar o teste de Wald com p coeficientes e p graus de liberdade.
Sabemos da subseção anterior que as séries são integradas de ordem 1, logo m é igual a 1. Nesses termos, vamos para o R montar o VAR em nível para as variáveis. Antes, vamos definir a quantidade de defasagens com a função VARselect do pacote vars.
def <- VARselect(data,lag.max=12,type="both")
Os critérios de informação retornaram 2, 3 e 6 defasagens. Vamos, então, construir o VAR com a função de mesmo nome do pacote vars, bem como testar se há autocorrelação com o Portmanteau Test, implementado na função serial.test.
### VAR(2) var2 <- VAR(data, p=2, type='both') serial.test(var2) ### VAR(3) var3 <- VAR(data, p=3, type='both') serial.test(var3) ### VAR(6) var6 <- VAR(data, p=6, type='both') serial.test(var6)
O VAR(6) parece ter menos problemas de autocorrelação. Com efeito, vamos adicionar m ao VAR(6), de modo a ter um VAR(7). Desse modo, agora assim, podemos proceder o teste de Wald. O código abaixo faz isso.
var7 <- VAR(data, p=7, type='both') ### Wald Test 01: FBCF não granger causa BNDES wald.test(b=coef(var7$varresult[[1]]), Sigma=vcov(var7$varresult[[1]]), Terms=c(2,4,6,8,10,12)) ### Wald Test 02: BNDES não granger causa FBCF wald.test(b=coef(var7$varresult[[2]]), Sigma=vcov(var7$varresult[[2]]), Terms= c(1,3,5,7,9,11))
Em ambos os testes, não podemos rejeitar a hipótese nula. Em outras palavras, não encontramos evidências de que os desembolsos do BNDES granger causam a taxa de investimento ou vice-versa. Significa dizer, leitor, que nossos resultados são conflitantes. Ora, se encontramos evidências de que as séries são cointegradas, deveríamos ter encontrado causalidade em ao menos uma direção. O motivo desse conflito pode estar no tamanho da série, que pode não ter sido suficiente para garantir a distribuição assintótica dos testes. O exercício, por fim, tem meros objetivos didáticos, de modo a mostrar como usar o R para verificar a relação entre duas séries. Mais exercícios podem ser encontrados no Clube do Código e no Códigos de Inverno 2016!
____________________________________________________________
(*) As referências do exercício estão no Códigos de Inverno 2016.
(**) Veja o código do exercício no repositório aberta da Análise Macro no GitHub aqui. É o exercício04.Rnw.