[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
A edição 36 do Clube do Código detalha a construção de um modelo preditivo para a taxa de desemprego medida pela PNAD Contínua. No modelo básico, os preditores utilizados foram a variação interanual da população ocupada e da população economicamente ativa. Em um modelo alternativo, além desses, foi incluída a variável gtrends, que contém buscas pela palavra chave "empregos" no google trends. O objetivo foi tanto detalhar a construção dos modelos quanto avaliar a qualidade das previsões geradas, dividindo a amostra em uma subamostra de training e outra de teste/validação. Nesse post, resumimos os resultados encontrados.
Antes de mais nada, precisamos coletar as variáveis que vamos utilizar no processo de modelagem. Por sorte, todos os dados estão disponíveis via pacotes do R. O código abaixo, então, ilustra o processo de importação dos dados.
library(forecast)
library(ggplot2)
library(easyGgplot2)
library(ggthemes)
library(BMR)
library(xtable)
library(sidrar)
library(scales)
library(TStools)
library(gtrendsR)
library(xts)
library(gridExtra)
### Obter e tratar dados do SIDRA
pea = ts(get_sidra(api='/t/6318/n1/all/v/1641/p/all/c629/32386')$Valor,
start=c(2012,03), freq=12)
po = ts(get_sidra(api='/t/6320/n1/all/v/4090/p/all/c11913/96165')$Valor,
start=c(2012,03), freq=12)
desemprego = ts(get_sidra(api='/t/6381/n1/all/v/4099/p/all/d/v4099%201')$Valor,
start=c(2012,03), freq=12)
dpea = (pea/lag(pea,-12)-1)*100
dpo = (po/lag(po,-12)-1)*100
### Obter e tratar dados go GTrends
trends = gtrends('empregos', geo='BR')
gtrends = data.frame(time=trends$interest_over_time$date,
empregos=trends$interest_over_time$hits)
gtrends$time = as.Date(gtrends$time, format='%d/%m/%Y')
gtrends = xts(gtrends$empregos, order.by=gtrends$time)
gtrends = ts(apply.monthly(gtrends, FUN=mean), start=c(2012,10), freq=12)
### Colocar tudo no mesmo objeto
data = ts.intersect(desemprego, dpo, dpea, gtrends)
colnames(data) = c('Desemprego', 'Variação PO', 'Variação PEA', 'GTrends')
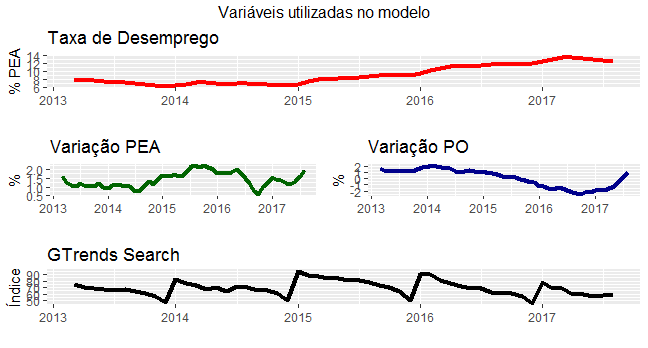
De posse dos dados, procedemos uma visualização gráfica dos mesmos.
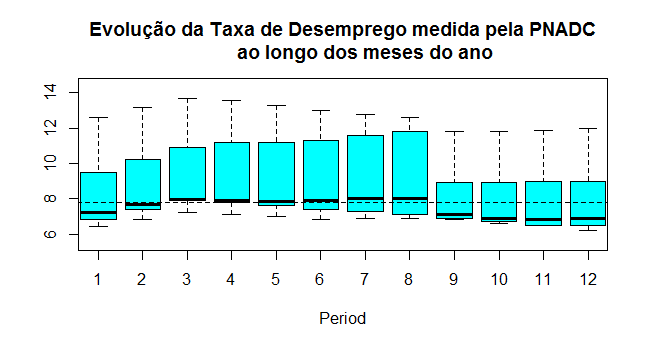
Para esse exercício, mantivemos os dados em seu formato original, isto é, não procedemos nenhum processo de dessazonalização ou diferenciação. A título de ilustração, o gráfico abaixo mostra como a taxa de desemprego se comporta ao longo dos meses do ano.
Com os dados coletados e tratados, podemos agora conhecer melhor os mesmos através das funções de autocorrelação, antes de proceder a modelagem em si.
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="4_4"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/06/woold.png" show_in_lightbox="off" url="https://analisemacro.com.br/clube-do-codigo/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
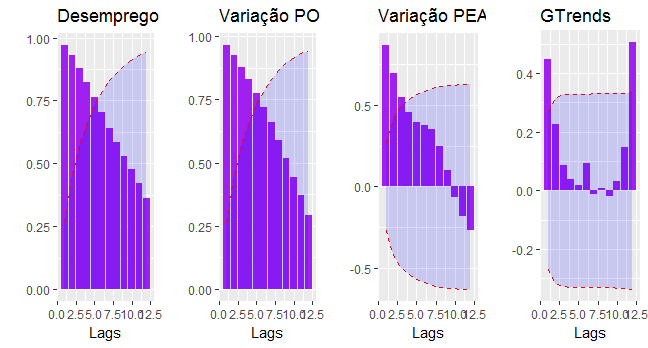
Abaixo, plotamos as funções de autocorrelação fazendo uso do pacote BMR.
E agora, as funções de autocorrelação parcial.
Com efeito, podemos agora gerar os modelos. Nesse exercício, optamos por construir um modelo bayesiano, utilizando o Normal-inverse-Wishhart como prior. As tabelas abaixo resumem as previsões dos dois modelos considerados nesse exercício.
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_code admin_label="Código"]<!-- html table generated in R 3.4.1 by xtable 1.8-2 package --> <!-- Mon Oct 09 03:10:21 2017 --> <table border=1> <caption align="bottom"> Previsões geradas pelo BVAR - Sem GTrends </caption> <tr> <th> </th> <th> Lower </th> <th> Mediana </th> <th> Upper </th> </tr> <tr> <td align="right"> set/17 </td> <td align="right"> 12.2 </td> <td align="right"> 12.4 </td> <td align="right"> 12.6 </td> </tr> <tr> <td align="right"> out/17 </td> <td align="right"> 11.8 </td> <td align="right"> 12.1 </td> <td align="right"> 12.5 </td> </tr> <tr> <td align="right"> nov/17 </td> <td align="right"> 11.3 </td> <td align="right"> 11.8 </td> <td align="right"> 12.3 </td> </tr> <tr> <td align="right"> dez/17 </td> <td align="right"> 10.8 </td> <td align="right"> 11.4 </td> <td align="right"> 12.1 </td> </tr> <tr> <td align="right"> jan/18 </td> <td align="right"> 10.3 </td> <td align="right"> 11.0 </td> <td align="right"> 11.8 </td> </tr> <tr> <td align="right"> fev/18 </td> <td align="right"> 9.7 </td> <td align="right"> 10.6 </td> <td align="right"> 11.5 </td> </tr> <tr> <td align="right"> mar/18 </td> <td align="right"> 9.0 </td> <td align="right"> 10.1 </td> <td align="right"> 11.2 </td> </tr> <tr> <td align="right"> abr/18 </td> <td align="right"> 8.3 </td> <td align="right"> 9.5 </td> <td align="right"> 10.8 </td> </tr> <tr> <td align="right"> mai/18 </td> <td align="right"> 7.6 </td> <td align="right"> 9.0 </td> <td align="right"> 10.5 </td> </tr> <tr> <td align="right"> jun/18 </td> <td align="right"> 6.7 </td> <td align="right"> 8.4 </td> <td align="right"> 10.1 </td> </tr> </table>[/et_pb_code][/et_pb_column][et_pb_column type="1_2"][et_pb_code admin_label="Código"]<!-- html table generated in R 3.4.1 by xtable 1.8-2 package --> <!-- Mon Oct 09 03:12:30 2017 --> <table border=1> <caption align="bottom"> Previsões geradas pelo BVAR - Com GTrends </caption> <tr> <th> </th> <th> Lower </th> <th> Mediana </th> <th> Upper </th> </tr> <tr> <td align="right"> set/17 </td> <td align="right"> 11.9 </td> <td align="right"> 12.1 </td> <td align="right"> 12.3 </td> </tr> <tr> <td align="right"> out/17 </td> <td align="right"> 11.2 </td> <td align="right"> 11.6 </td> <td align="right"> 12.0 </td> </tr> <tr> <td align="right"> nov/17 </td> <td align="right"> 10.4 </td> <td align="right"> 11.1 </td> <td align="right"> 11.7 </td> </tr> <tr> <td align="right"> dez/17 </td> <td align="right"> 9.6 </td> <td align="right"> 10.5 </td> <td align="right"> 11.4 </td> </tr> <tr> <td align="right"> jan/18 </td> <td align="right"> 8.7 </td> <td align="right"> 9.9 </td> <td align="right"> 11.0 </td> </tr> <tr> <td align="right"> fev/18 </td> <td align="right"> 7.8 </td> <td align="right"> 9.3 </td> <td align="right"> 10.6 </td> </tr> <tr> <td align="right"> mar/18 </td> <td align="right"> 6.8 </td> <td align="right"> 8.6 </td> <td align="right"> 10.3 </td> </tr> <tr> <td align="right"> abr/18 </td> <td align="right"> 5.7 </td> <td align="right"> 7.9 </td> <td align="right"> 9.8 </td> </tr> <tr> <td align="right"> mai/18 </td> <td align="right"> 4.6 </td> <td align="right"> 7.1 </td> <td align="right"> 9.4 </td> </tr> <tr> <td align="right"> jun/18 </td> <td align="right"> 3.4 </td> <td align="right"> 6.3 </td> <td align="right"> 9.0 </td> </tr> </table>[/et_pb_code][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
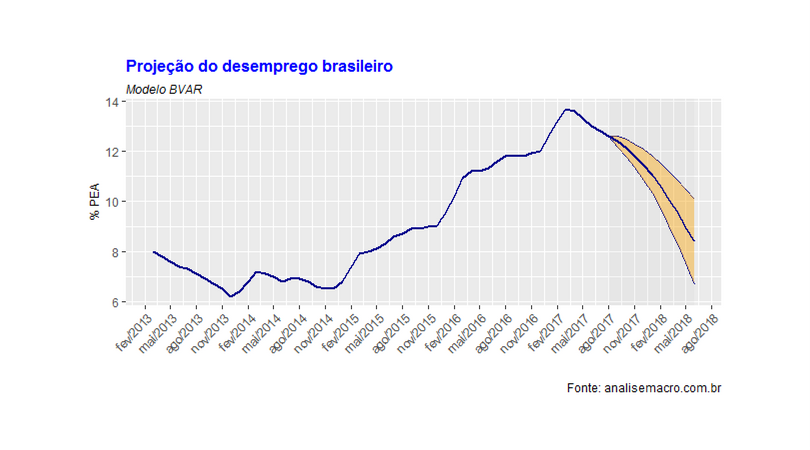
A adição da variável gtrends acaba gerando um viés nas projeções, piorando as medidas de acurácia. Desse modo, não nos pareceu válido o esforço de adicionar essa variável na modelagem da taxa de desemprego. Ao menos, não na abordagem que consideramos. Ficamos, portanto, com o modelo base. O gráfico abaixo ilustra as projeções 10 meses à frente.
Os membros do Clube do Código têm acesso a todo o processo de construção das previsões, brevemente descrito nesse post. Para se tornar membro, consulte a página do Clube aqui.
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/06/liberte-se.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][et_pb_text admin_label="Texto" background_layout="light" text_orientation="center" use_border_color="off" border_color="#ffffff" border_style="solid"]
Clique na figura para conhecer os nossos Cursos
[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/04/painel.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/cursos-de-econometria/dados-em-painel/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][et_pb_text admin_label="Texto" background_layout="light" text_orientation="center" use_border_color="off" border_color="#ffffff" border_style="solid"] Clique na figura para conhecer nosso novo curso de econometria [/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_3"][et_pb_gallery admin_label="Galeria" gallery_ids="17132,17133,17134" fullwidth="on" show_title_and_caption="off" show_pagination="off" background_layout="light" auto="on" auto_speed="6000" hover_overlay_color="rgba(255,255,255,0.9)" caption_all_caps="off" use_border_color="off" border_color="#ffffff" border_style="solid" saved_tabs="all"] [/et_pb_gallery][et_pb_gallery admin_label="Galeria" gallery_ids="17136,17137,17138" fullwidth="on" show_title_and_caption="off" show_pagination="off" background_layout="light" auto="on" auto_speed="6000" hover_overlay_color="rgba(255,255,255,0.9)" caption_all_caps="off" use_border_color="off" border_color="#ffffff" border_style="solid" saved_tabs="all"] [/et_pb_gallery][/et_pb_column][et_pb_column type="2_3"][et_pb_team_member admin_label="Pessoa" saved_tabs="all" name="Vítor Wilher " position="Data Scientist" animation="left" background_layout="light" facebook_url="https://www.facebook.com/vitor.wilher.9" twitter_url="https://twitter.com/vitorwilherbr" linkedin_url="https://www.linkedin.com/in/v%C3%ADtor-wilher-78164024" use_border_color="off" border_color="#ffffff" border_style="solid"]
Vítor Wilher é Bacharel e Mestre em Economia, pela Universidade Federal Fluminense, tendo se especializado na construção de modelos macroeconométricos, política monetária e análise da conjuntura macroeconômica doméstica e internacional. Tem, ademais, especialização em Data Science pela Johns Hopkins University. Sua dissertação de mestrado foi na área de política monetária, titulada "Clareza da Comunicação do Banco Central e Expectativas de Inflação: evidências para o Brasil", defendida perante banca composta pelos professores Gustavo H. B. Franco (PUC-RJ), Gabriel Montes Caldas (UFF), Carlos Enrique Guanziroli (UFF) e Luciano Vereda Oliveira (UFF). Já trabalhou em grandes empresas, nas áreas de telecomunicações, energia elétrica, consultoria financeira e consultoria macroeconômica. É o criador da Análise Macro, startup especializada em treinamento e consultoria em linguagens de programação voltadas para data analysis, sócio da MacroLab Consultoria, empresa especializada em cenários e previsões e fundador do hoje extinto Grupo de Estudos sobre Conjuntura Econômica (GECE-UFF). É também Visiting Professor da Universidade Veiga de Almeida, onde dá aulas nos cursos de MBA da instituição, Conselheiro do Instituto Millenium e um dos grandes entusiastas do uso do R no ensino. Leia os posts de Vítor Wilher aqui. Caso queira, mande um e-mail para ele: vitorwilher@analisemacro.com.br
[/et_pb_team_member][/et_pb_column][/et_pb_row][/et_pb_section]