A Edição 61 do Clube do Código, que estará disponível para os membros essa semana no repositório privado, busca estimar um modelo via mínimos quadrados parciais para o IFIX, o Índice de Fundos de Investimentos Imobiliários. Segundo a B3, "O IFIX é o resultado de uma carteira teórica de ativos, elaborada de acordo com os critérios estabelecidos nesta metodologia. O objetivo do IFIX é ser o indicador do desempenho médio das cotações dos fundos imobiliários negociados nos mercados de bolsa e de balcão organizado da B3".
A opção por mínimos quadrados parciais para modelar a variável se dá devido a grande quantidade de preditores utilizados, entre variáveis reais de desempenho da economia brasileira e variáveis eminentemente financeiras, com relação entre si. A modelagem via mínimos quadrados ordinários implicaria, assim, em problemas de multicolinearidade.
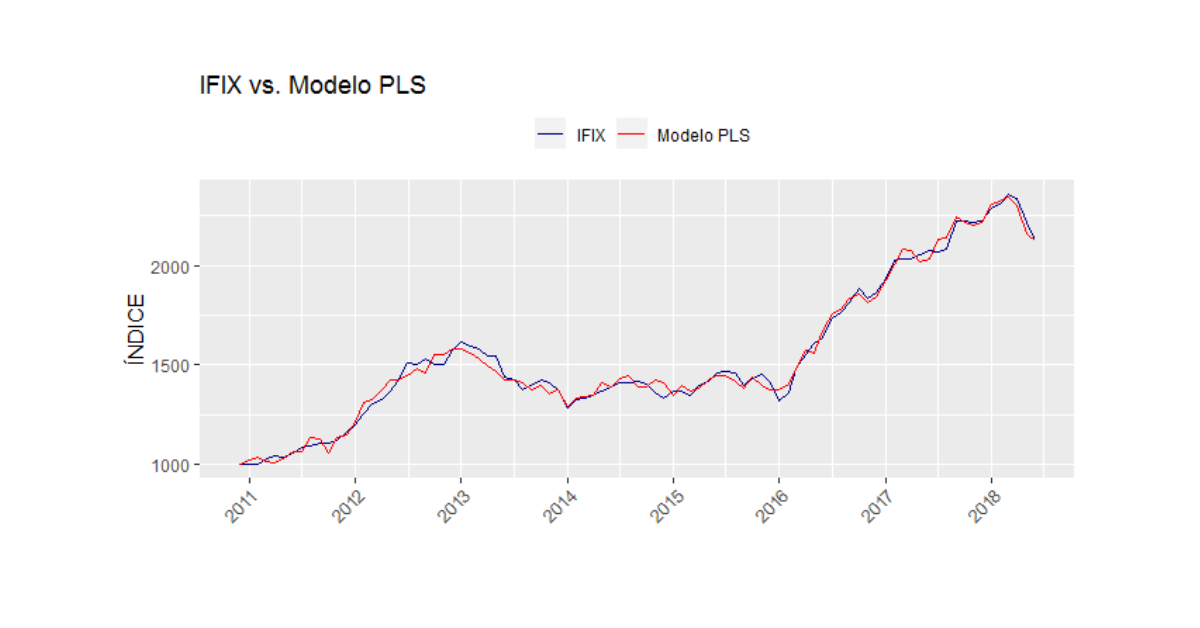
Uma vez escolhidos os preditores e estimado o modelo dentro da amostra de treino, o ajuste do modelo nos pareceu satisfatório, como mostra o gráfico acima. Isso foi confirmado por medidas de acurácia avaliadas na amostra de teste.
____________________________
O Clube do Código é o projeto de compartilhamento de códigos da Análise Macro. Conheça e apoie o projeto!