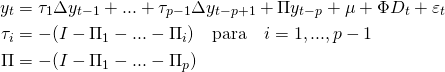[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
A trajetória da Dívida Bruta brasileira tem sido objeto de preocupação entre analistas e investidores. Exemplo disso foi o rebaixamento da nota de crédito do país pelas três principais agências de classificação de risco. Mas o que está por trás do aumento da relação Dívida/PIB? Quais são os determinantes do endividamento público? Como podemos modelar essa relação ao longo do tempo? Melhor: como podemos prever essa relação para os próximos meses? São essas e outras questões que abordamos em uma das seções do nosso Curso de Macroeconometria usando o R e na edição 33 do Clube do Código. Para isso, construímos um Modelo Vetor de Correção de Erros (VECM).
Com o código abaixo, nós coletamos os dados que utilizaremos, bem como fazemos os tratamentos necessários para tornar os dados comparáveis.
### Coletar os dados
dbgg = window(BETS.get(13762), start=c(2007,01))
selic = window(BETS.get(4189), start=c(2007,01))
inflacao = window(BETS.get(13522), start=c(2007,01))
pib = BETS.get(22099)
nfsp = window(BETS.get(5793), start=c(2007,01))
cambio = window(BETS.get(3697), start=c(2007,01))
### Construir variáveis
dpib = (((pib+lag(pib,-1)+lag(pib,-2)+lag(pib,-3))/4)/
((lag(pib,-4)+lag(pib,-5)+lag(pib,-6)+lag(pib,-7))/4)-1)*100
juroreal = (((1+(selic/100))/(1+(inflacao/100)))-1)*100
### Juntar os dados mensais
data = ts.intersect(dbgg, juroreal, nfsp, cambio)
### Trimestralizar
data = ts(aggregate(data, nfrequency=4, FUN=mean),
start=c(2007,01), freq=4)
### Juntar todos os dados
data = ts.intersect(data, dpib)
colnames(data) = c('dbgg', 'juroreal', 'nfsp', 'cambio', 'dpib')
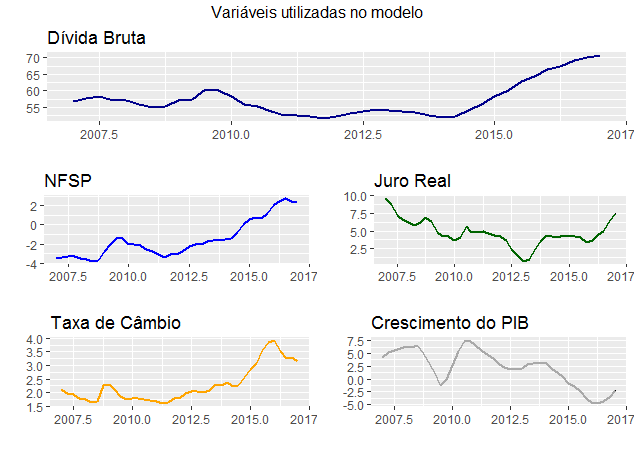
Abaixo, visualizamos as séries.
Com os dados coletados e tratados, podemos iniciar o nosso exercício.
Construindo um Vetor de Correção de Erros
De forma a gerar um modelo para a Dívida Bruta, nós vamos construir um Vetor de Correção de Erros (VECM), uma vez que todas as séries são não estacionárias. Para isso, vamos nos basear no exercício realizado por Johansen e Juselius (1992), onde os autores utilizam um contexto de cointegração multivariada. Para começar, podemos especificar, como em Pfaff (2008) uma versão de um VECM, onde , um vetor
de séries no período
entram com defasagem
:
(1)
onde é uma matriz
de coeficientes das variáveis endógenas defasadas,
é um vetor
de constantes,
é um vetor de variáveis não estocásticas,
é a matriz identidade
,
é a matriz que contém os impactos cumulativos de longo prazo e, por fim,
é o vetor
de termos de erros, supostamente i.i.d. tal que
.
Uma vez especificado o modelo, passamos agora à fase prática. Existe, afinal, cointegração entre as séries envolvidas? Utilizamos o teste de Johansen abaixo para verificar.
### Selecionar Defasagem def = VARselect(data,lag.max=12,type="both") ### Teste de Cointegração Máximo AutoValor jo.eigen = ca.jo(data, type='eigen', K=5, ecdet='const', spec='transitory')
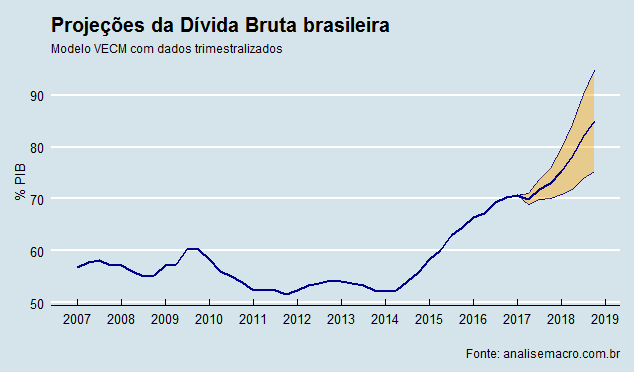
Não podemos rejeitar a existência de três vetores de cointegração pelo teste do máximo autovalor. Com efeito, montamos o VECM e geramos as previsões. Abaixo um gráfico que ilustra a projeção da Dívida Bruta do 2º trimestre de 2017 ao quarto trimestre de 2018. Pelo modelo estimado, a Dívida Bruta chega a 85% no final do período.
[/et_pb_text][/et_pb_column][/et_pb_row][/et_pb_section]