Diversos analistas e economistas têm notado o aumento na margem dos indicadores de confiança de consumidores e empresários. De forma intuitiva, é possível dizer que uma melhora da confiança tende a antecipar o aumento do consumo e da produção. Nesse post, por suposto, queremos verificar através do procedimento de Toda e Yamamoto (1995) se é possível dizer que o indicador de confiança industrial tem precedência temporal sobre o índice de produção industrial. Como sempre, membros do Clube do Código têm acesso ao script e aos dados utilizados nesse exercício no repositório privado do GitHub - é preciso estar logado no GitHub para ter acesso ao repositório.
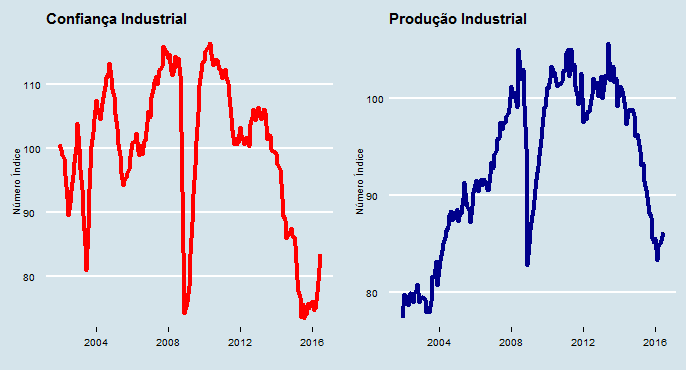
As séries utilizadas nesse exercício foram o Índice de Confiança Industrial com ajuste sazonal da Fundação Getúlio Vargas (FGV) e o índice da produção industrial geral, também com ajuste sazonal, fornecido pelo Instituto Brasileiro de Geografia e Estatítisca (IBGE). A amostra vai de janeiro de 2002 a junho de 2016, totalizando 176 observações.
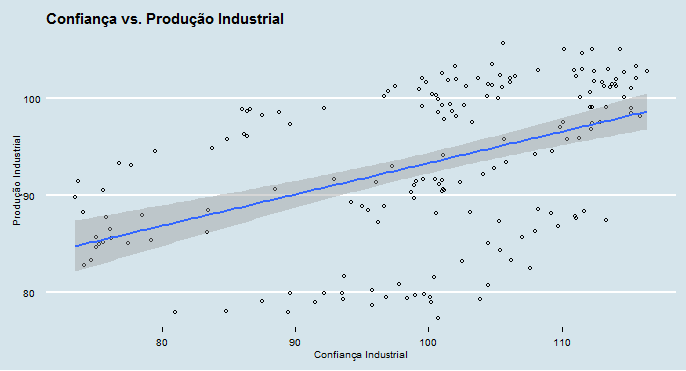
De modo a investigar a relação entre as séries ao longo do tempo, primeiro nós verificamos a correlação. Como se depreende do gráfico acima, é possível verificar uma correlação positiva entre as séries, como era de se suspeitar. Adiante, quisemos verificar se existiria causalidade nessa relação.
Os testes de raiz unitária, que podem ser vistos aqui, mostraram que teríamos problemas caso aplicássemos o teste de Granger clássico. A produção industrial parece ser um passeio aleatório sem drift, enquanto a confiança parece ser uma série tendência-estacionária. Com efeito, recorremos ao procedimento de Toda e Yamamoto (1995) para verificar a existência de causalidade.
Um exemplo completo da aplicação do procedimento pode ser visto aqui. Abaixo, colocamos o resultado final do teste de Wald.
### Teste de Wald var5 <- VAR(data, p=5, type='both') ### Wald Test 01: Confiança não granger causa Produção Industrial wald.test(b=coef(var5$varresult[[1]]), Sigma=vcov(var5$varresult[[1]]), Terms=c(2,4,6,8)) ### Wald Test 02: Produção Industrial não granger causa Confiança wald.test(b=coef(var5$varresult[[2]]), Sigma=vcov(var5$varresult[[2]]), Terms= c(1,3,5,7))
O teste empírico nos permite afirmar que, de fato, existe causalidade na relação entre confiança e produção industrial. Isto é, a confiança granger causa a produção industrial, enquanto não é possível afirmar o mesmo no caso contrário. Desse modo, a recente melhora nos índices de confiança pode ser um sinal de que, de fato, há alguma perspectiva positiva para a produção industrial em 2016... Após um longo inverno, como mostrado no gráfico acima... 🙂
_____________________________________________________
Toda, H. Y., Yamamoto, T. (1995). Statistical Inference in vector autoregressions with possibly integrated process, Journal of Econometrics, 66:225-250.