Laura Carvalho vs. Ilan Goldfajn: quem tem razão?

[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

Todos os anos, o Banco Central publica em seu Relatório Trimestral de março uma decomposição da inflação ocorrida no ano anterior. Isto é, ele busca ilustrar a contribuição de alguns "fatores" para a inflação no período. Laura Carvalho, professora da FEA-USP, utilizou esse exercício para refutar a "tese" do presidente da autoridade monetária, para quem a mudança na equipe econômica teria "quebrado a espinha dorsal da inflação". Nesse embate, quem está certo: Laura ou Ilan?

[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/09/cliqueaqui.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]

[/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

Em sua coluna de ontem na Folha, Laura teve o cuidado de não fazer menção ao aumento da inércia inflacionária entre 2015 e 2016, mostrado no mesmo exercício do Banco Central. Certamente, porque isso causaria embaraços à sua narrativa. Nesse post, explico os motivos. Antes, por suposto, é de bom tom dizer ao leitor que a inflação no curto prazo pode ser explicada conforme a seguinte equação

(1) $\begin{equation*} \pi_t = \alpha_0 + \alpha_1 \pi_{t-1} + \alpha_2 E_t \pi_{t+1} + \alpha_3 h_t + \alpha_4 \Delta e_t + \varepsilon_t \end{equation*}$

onde $\pi_t$ é a inflação, $E_t \pi_{t+1}$ é a expectativa de inflação para o próximo período, $h_t$ é o hiato do produto, $\Delta e_t$ é a primeira diferença da taxa de câmbio e $\varepsilon_t$ um termo de erro, supostamente um ruído branco. Isso dito, observemos a inflação acumulada em 12 meses medida pelo IPCA nos últimos anos no gráfico abaixo.

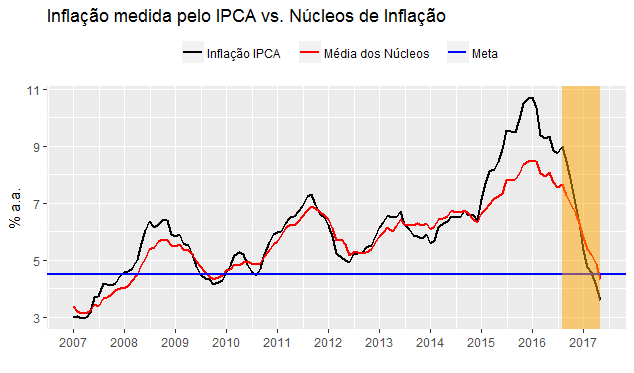
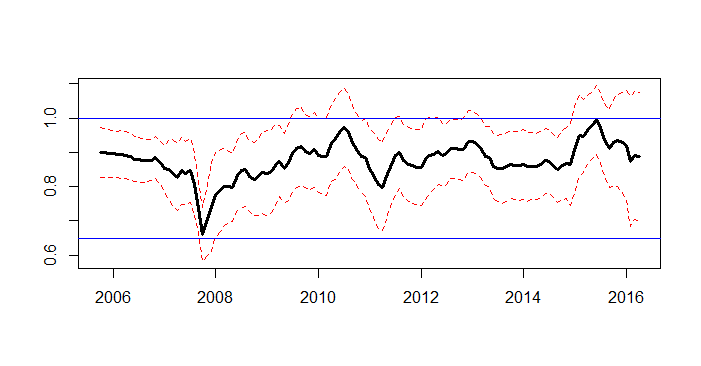
Além da inflação, o gráfico também traz a média dos cinco núcleos construídos e divulgados pelo Banco Central mensalmente. A ideia de um núcleo de inflação é basicamente retirar fatores idissiocráticos, concentrando-se na tendência de longo prazo da inflação. O que fica nítido no gráfico acima, por suposto, é que a inflação medida pelo IPCA encontrava-se em elevação desde 2010, distanciando-se assim da meta, ilustrada pela linha azul.

Esse comportamento da inflação, diga-se, tem nítidos efeitos sobre os agentes econômicos. O mais óbvio é que a meta de inflação deixa de ser uma âncora, bem como a inflação passada ganha importância na determinação da taxa de crescimento dos preços. Isso, a propósito, pode ser capturado pela estimação da equação (1). Acaso o leitor interessado fizer o exercício, irá verificar que o coeficiente do componente regressivo $\pi_{t-1}$ , isto é, da inflação passada, passará a ter maior importância para explicar o crescimento dos preços. O gráfico abaixo ilustra, no exercício que fizemos no Clube do Código sobre assunto.

O aumento da inércia torna a desinflação do organismo econômico muito mais custosa, em termos de hiato do produto e, portanto, de taxa de desemprego. É justamente por isso que é prejudicial desviar de forma rotineira da meta de inflação, dado que isso contribui inexoravelmente para o aumento da inércia inflacionária. Isso dito, o que podemos dizer sobre as alegações de Laura Carvalho em relação ao que disse o presidente do BC?

Laura Carvalho se baseia no exercício de decomposição da inflação do Banco Central para confrontar o que disse Ilan, mas isso faz pouco sentido se considerarmos os parágrafos anteriores. O presidente da autoridade monetária fez referência justamente à quebra da inércia, medida pela convergência das expectativas de inflação para a meta. Laura, por seu turno, se concentra em uma avaliação contábil da inflação, deixando cuidadosamente de lado o aumento da inércia no período.

Isso não é correto, uma vez que esse aumento da inércia está associado justamente aos erros de condução da política econômica no período anterior a Ilan. Dentre esses erros, cabe mencionar o controle dos preços administrados de forma paralela à redução forçada da taxa de juros. Em outras palavras, em algum momento entre 2011-2013, o governo resolveu acreditar em mecanismos não monetários de controle da inflação, levando a mesma à tendência crescente ilustrada no primeiro gráfico.

A volta aos cânones da profissão, patrocinada pela nova equipe econômica, fez com que a inflação efetiva convergisse de forma mais rápida para a meta, como pode ser visto na área hachurada do primeiro gráfico. Certamente, a inflação cederia, dada a abertura do hiato do produto, mas provavelmente não com a velocidade verificada, uma vez que era preciso romper com o aumento da inércia dos últimos anos e, ademais, a taxa de câmbio dificilmente teria se valorizado do jeito que se valorizou com a equipe econômica anterior.

Em assim sendo, leitor, não me parece que a professora da FEA USP tenha refutado o presidente da autoridade monetária, dado que cuidadosamente evitou discorrer sobre o aumento da inércia inflacionária nos últimos anos. Talvez fosse o caso de fazê-lo em sua próxima coluna... 🙂

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha" make_fullwidth="off" use_custom_width="off" width_unit="on" use_custom_gutter="off" padding_mobile="off" allow_player_pause="off" parallax="off" parallax_method="off" make_equal="off" parallax_1="off" parallax_method_1="off" column_padding_mobile="on"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

_____________________________________________________________________

Apêndice: Código no R que gerou o gráfico "Inflação medida pelo IPCA vs. Núcleos de Inflação".

## Importar séries do Banco Central diretamente para o R
library(BETS)
series = c(433, 4466, 11426, 11427, 16121, 16122)
dates = seq(as.Date('2006-02-01'), as.Date('2017-05-01'), by='1 month')
data = matrix(NA, nrow=length(dates), ncol=length(series))
colnames(data) = c('ipca', 'n1', 'n2', 'n3', 'n4', 'n5')

for(i in 1:length(series)){

  data[,i] = BETS.get(series[i], from = '2006-02-01', to='2017-05-01')
  
}

data = ts(data, start=c(2006,02), freq=12)

## Acumular em 12 meses
fator = 1+data/100
acumulado = (fator*lag(fator,-1)*lag(fator,-2)*lag(fator,-3)*
                lag(fator,-4)*lag(fator,-5)*lag(fator,-6)*lag(fator,-7)*
                lag(fator,-8)*lag(fator,-9)*lag(fator,-10)*lag(fator,-11)
              -1)*100
colnames(acumulado) = colnames(data)

## Fazer o gráfico
library(forecast)
library(ggplot2)
library(scales)

nucmean = rowMeans(acumulado[,2:6])
dates = seq(as.Date('2007-01-01'), as.Date('2017-05-01'), by='1 month')
df = data.frame(time=dates, ipca=acumulado[,1], nucmean=nucmean)
ggplot(df, aes(x=time))+
  geom_line(aes(y=ipca, colour='Inflação IPCA'), size=.8)+
  geom_line(aes(y=nucmean, colour='Média dos Núcleos'), size=.8)+
  geom_hline(aes(yintercept=4.5, colour='Meta'), size=.8)+
  scale_colour_manual('', values=c('Inflação IPCA'='black',
                                   'Média dos Núcleos'='red',
                                   'Meta'='blue'))+
  theme(legend.position = 'top')+
  xlab('')+ylab('% a.a.')+
  labs(title='Inflação medida pelo IPCA vs. Núcleos de Inflação')+
 scale_x_date(breaks = date_breaks('1 years'),
 labels = date_format('%Y'))+
 annotate('rect', fill = 'orange', alpha = 0.5, 
 xmin = as.Date('2016-08-01'), 
 xmax = as.Date('2017-05-01'),
 ymin = -Inf, ymax = Inf)

[/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/09/cliqueaqui.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/cursos-de-econometria/" url_new_window="off" use_overlay="off" animation="off" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]

[/et_pb_image][/et_pb_column][/et_pb_row][/et_pb_section]

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise exploratória e seleção de séries temporais econômicas para modelagem

Transformers para Análise de Séries Temporais

O que é e como funciona a Arquitetura Transformer

Tratamento e transformação de séries temporais macroeconômicas para modelagem

Como planejar um pipeline de previsão macroeconômica: da coleta ao dashboard

Coletando e integrando dados do BCB, IBGE e IPEA de forma automatizada

Outros artigos relacionados

Análise exploratória e seleção de séries temporais econômicas para modelagem

Quer entender como transformar dados econômicos brutos em previsões macroeconômicas precisas? Neste post, mostramos passo a passo como realizar a análise exploratória e seleção de séries temporais com Python — desde o tratamento de dados e remoção de multicolinearidade até a escolha das variáveis mais relevantes usando técnicas de machine learning e econometria. Um guia essencial para quem quer unir teoria econômica e inteligência artificial na prática da previsão macroeconômica.

Transformers para Análise de Séries Temporais

Nesse tutorial ensinamos como podemos aplicar dados de séries temporais na arquitetura Transformer através de biblioteca no Python, como darts, GluonTS e Hugging Face.

O que é e como funciona a Arquitetura Transformer

Nesse tutorial ensinamos como é o funcionamento da arquitetura Transformer.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!