Séries Temporais e a Evolução da Modelagem de Sequências
Analisar uma série temporal é, em essência, uma forma de “modelagem de sequências”. O objetivo é entender os padrões em dados ordenados no tempo para prever o que virá a seguir, e os diferentes tipos de modelos criados ao longo da história da análise de séries temporais até o dias atuais é extensivo.
Entre alguns deles, temos:
- Modelos Clássicos (Ex: ARIMA): Eficazes para séries com padrões lineares e estacionários, mas limitados ao capturar relações mais complexas e não-lineares.
- Redes Neurais Recorrentes (Ex: RNNs): Introduziram o conceito de “memória”, processando sequências passo a passo e mantendo um estado interno. No entanto, sofriam para reter informações de longo prazo, um problema conhecido como gradiente descendente.
- LSTMs e GRUs: Variações das RNNs com “portões” (gates) que controlam o fluxo de informação, melhorando a capacidade de aprender dependências de longo prazo. Apesar do grande avanço, elas ainda processam os dados de forma sequencial, o que pode ser um gargalo computacional.
É neste ponto que os Transformers surgem, quebrando o paradigma do processamento sequencial e introduzindo uma forma mais poderosa de “lembrar” o passado: a atenção.
* Caso deseje aprender mais sobre o que é Transformers, veja esse post.
Objetivo
Para obter o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Mostraremos como aplicar esses conceitos em séries temporais usando a biblioteca darts. O foco será em entender a lógica por trás do uso prático dessa tecnologia.
Transformers em Séries Temporais: Como é Possível?
A transição dos Transformers do texto para as séries temporais é conceitualmente direta. Em NLP, um Transformer trata cada palavra (ou “token”) em uma frase como uma unidade. Em uma série temporal, cada observação (ex: o valor diário do câmbio) é tratada como um “token”.
A sequência de valores ao longo do tempo se torna uma “frase”, e o Transformer aprende a gramática e o contexto dessa “frase” temporal.
# Exemplo simbólico: sequência temporal como "frases"
# Cada valor é um "token" que o Transformer analisa em relação aos outros.
serie_juros = [12.50, 12.75, 13.25, 13.75, 13.75, 13.25, 12.75]
# O Transformer pode aprender que a primeira ocorrência de 12.75,
# mesmo distante, é um forte indicador para a ocorrência futura de 13.25,
# ignorando os valores intermediários se não forem relevantes.Adaptar uma arquitetura de texto para números ordenados no tempo parece um salto, mas a analogia é direta: uma série temporal é tratada como uma frase, onde cada observação é uma palavra.
No entanto, essa adaptação traz desafios, vantagens e desvantagens.
Os Desafios e as Soluções
- Problema: Falta de Noção de Ordem. Como mencionado, o self-attention é invariante à permutação.
- Solução: O Positional Encoding é crucial. Ele injeta a informação temporal diretamente nos dados de entrada, permitindo que o modelo aprenda a importância da ordem.
- Problema: Complexidade Quadrática. O self-attention compara cada ponto com todos os outros. Para uma série com
Npontos, isso exigeN²cálculos. Para séries temporais muito longas (milhares ou milhões de pontos), isso se torna computacionalmente inviável.- Solução: Pesquisas recentes criaram variações mais eficientes, como o Informer e o LogSparse Transformer, que usam mecanismos de atenção “esparsos”, focando apenas nos pontos mais relevantes e reduzindo drasticamente a complexidade.
- Problema: Dados Contínuos vs. Discretos. Texto é formado por tokens discretos (palavras). Séries temporais são contínuas.
- Solução: Tratamos cada ponto de observação como um token discreto e o transformamos em um embedding, permitindo que o modelo opere sobre eles da mesma forma que faria com palavras.
Vantagens
- Captura de Dependências de Longo Prazo: Esta é a maior vantagem sobre LSTMs. Um Transformer pode, teoricamente, conectar um evento de hoje (ex: uma queda na bolsa) a uma crise financeira ocorrida há vários anos, simplesmente porque o mecanismo de atenção pode criar uma ligação direta entre esses dois pontos no tempo, sem que a informação se degrade ao longo do caminho.
- Paralelização: Ao contrário das RNNs, que precisam processar os dados sequencialmente, o Transformer processa a série inteira de uma vez. Isso o torna muito mais rápido para treinar em hardware moderno (GPUs/TPUs).
- Interpretabilidade: Os mapas de atenção podem ser visualizados, permitindo entender em quais pontos do passado o modelo está “prestando mais atenção” para fazer uma previsão, o que ajuda a abrir a “caixa-preta”.
Desvantagens
- Exigência de Dados: Transformers são modelos grandes com milhões de parâmetros. Eles precisam de grandes volumes de dados para serem treinados de forma eficaz e evitar o superajuste (overfitting).
- Complexidade (fora da caixa): Como mencionado, a complexidade quadrática torna o Transformer “vanilla” inadequado para séries temporais muito longas. É necessário recorrer a variantes mais complexas e recentes.
- Menos “Viés Indutivo” para o Tempo: RNNs são construídas com a premissa de sequencialidade. Transformers não têm essa premissa e dependem inteiramente do Positional Encoding para aprender a ordem. Em conjuntos de dados menores, essa falta de um viés estrutural pode levar a um desempenho inferior.
Darts
Darts é uma biblioteca Python de código aberto projetada para tornar a previsão e análise de séries temporais mais acessível e eficiente. Desenvolvida pela Unit8, ela oferece uma API consistente e simples, semelhante à do scikit-learn, que permite aos usuários aplicar uma vasta gama de modelos de previsão, desde os clássicos como ARIMA e Suavização Exponencial até modelos avançados de aprendizado profundo como LSTMs, N-BEATS e Transformers.
Principais Características:
- API Unificada: A principal vantagem do Darts é sua interface
fit()epredict()padronizada para todos os modelos, o que simplifica a experimentação e a comparação entre diferentes abordagens. - Suporte Amplo: Lida tanto com séries temporais univariadas quanto multivariadas e oferece suporte a previsões probabilísticas para quantificar a incerteza.
- Backtesting e Avaliação: Inclui ferramentas robustas para backtesting de modelos, permitindo simular previsões históricas em janelas de tempo móveis e avaliar a performance com diversas métricas.
- Integração: É compatível com estruturas de dados populares como Pandas DataFrames, NumPy arrays e PyTorch Tensors, facilitando a manipulação e o pré-processamento dos dados.
1. Instalação e Carregamento
Primeiro, vamos instalar a biblioteca. Você pode fazer isso com um simples comando pip. Depois de instalar, vamos importá-la para o nosso código.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
2. Criando Dados para Séries Temporais
A Darts trabalha com um objeto especial chamado TimeSeries. Ele é otimizado para manipulação de dados temporais. Vamos criar uma série temporal simples do zero para ver como funciona.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM

3. Exemplo Mínimo de Previsão
Agora que temos uma série temporal, vamos fazer uma previsão. Usaremos um modelo simples e clássico chamado ExponentialSmoothing (Suavização Exponencial).
O processo é sempre o mesmo, não importa o modelo: 1. Dividir os dados em treino e teste. 2. Criar uma instância do modelo. 3. Treinar o modelo com os dados de treino (fit()). 4. Fazer a previsão (predict()).
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM

4. Previsão com Transformer
Vamos agora realizar a previsão da mesma série através do módulo Transformer.
Modelos de redes neurais, como o Transformer, funcionam muito melhor quando os dados estão em uma escala semelhante, geralmente entre 0 e 1. Isso ajuda o modelo a aprender mais rápido e de forma mais estável. Vamos começar normalizando nossos dados de treino e validação.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
Configurando o Modelo Transformer
Vamos treinar uma arquitetura Transformer. Embora ela tenha muitos parâmetros, vamos ajustar alguns dos mais importantes para séries temporais com apenas uma variável:
- d_model: A dimensionalidade interna do modelo. O padrão é 512, um valor muito alto para uma série simples. Reduzimos para um valor menor, como 16, para evitar que o modelo se torne complexo demais.
- nhead: O número de “cabeças” no mecanismo de atenção múltipla. Aumentar este número permite que o modelo foque em diferentes padrões nos dados ao mesmo tempo.
O objetivo é realizar uma previsão de um passo à frente no tempo.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
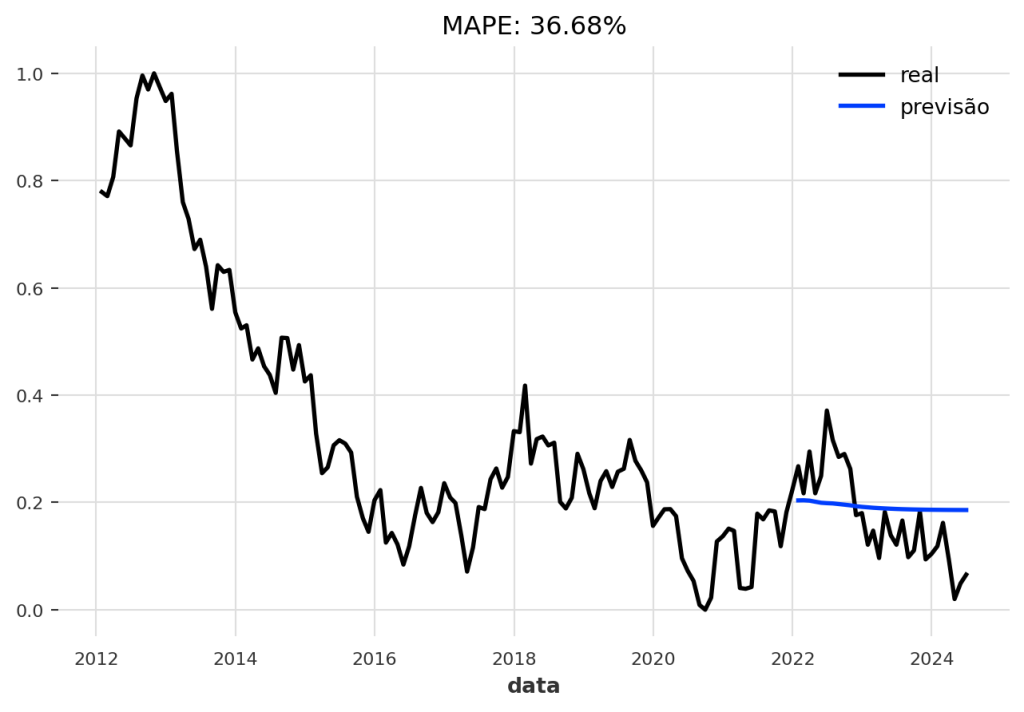
Avaliando o Modelo na Validação
Agora, vamos analisar as previsões no conjunto de validação. Para facilitar a visualização, vamos criar uma função que plota os dados reais, a previsão e o erro MAPE (Erro Percentual Absoluto Médio).
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
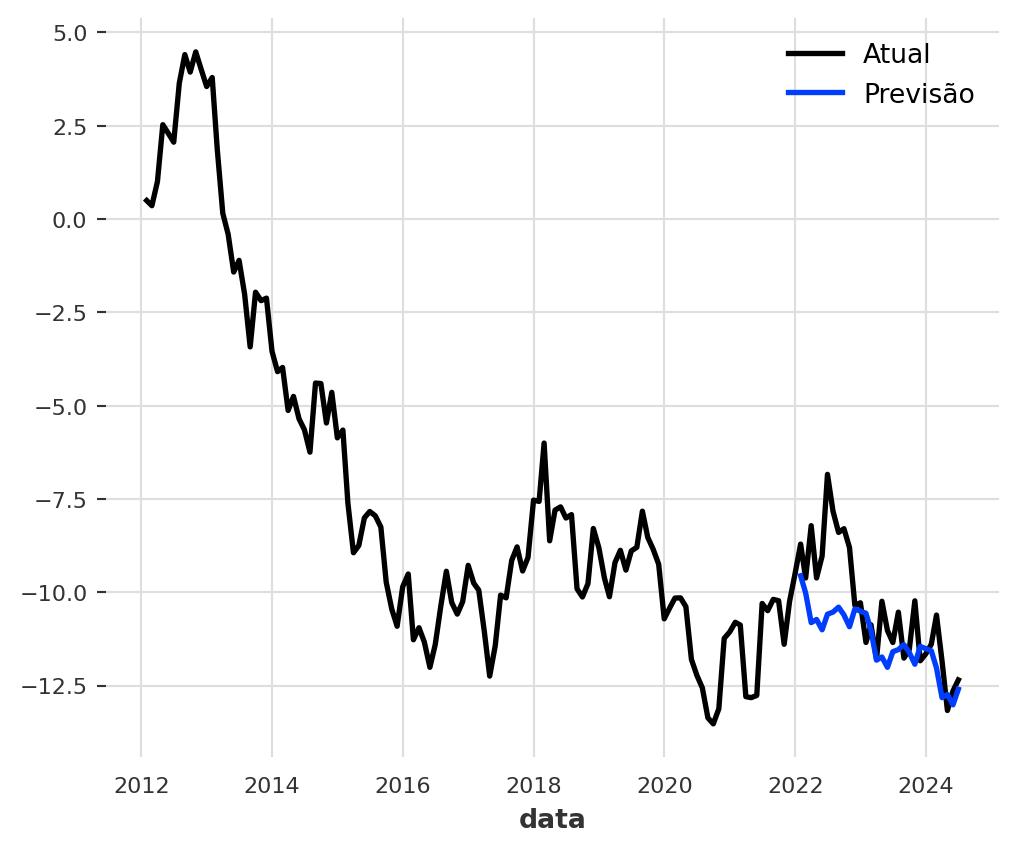
Primeiro, vamos usar o modelo “atual”, ou seja, o modelo ao final do procedimento de treinamento:
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
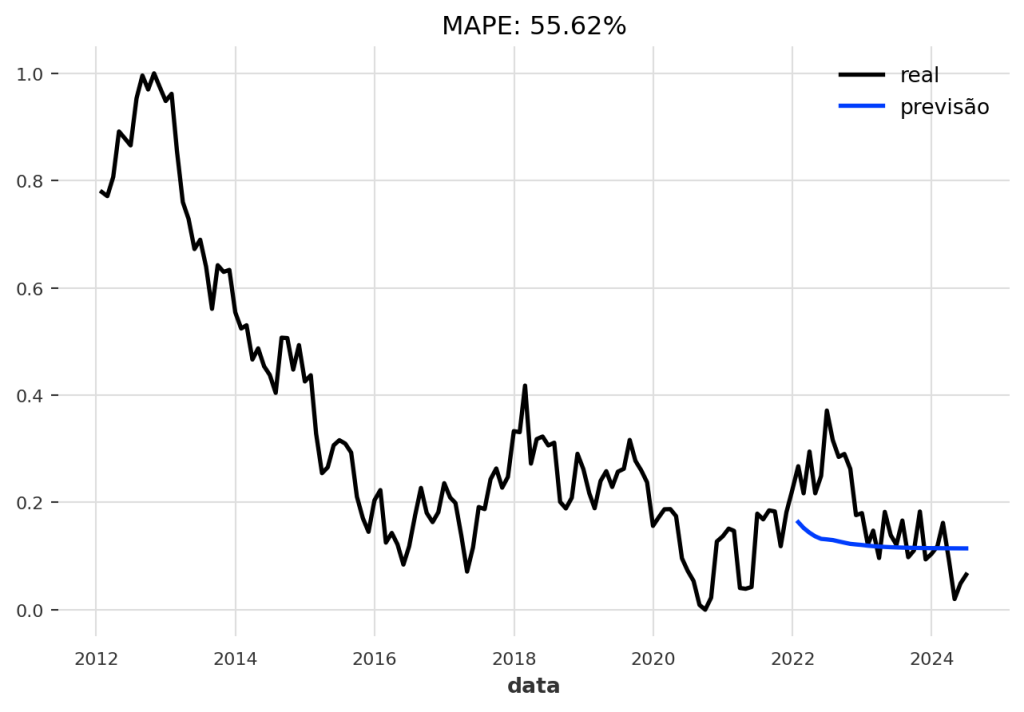
No entanto, é uma prática comum usar o modelo que teve o melhor desempenho no conjunto de validação durante o treinamento, e não necessariamente o último. A Darts salva este “melhor modelo” automaticamente para nós.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
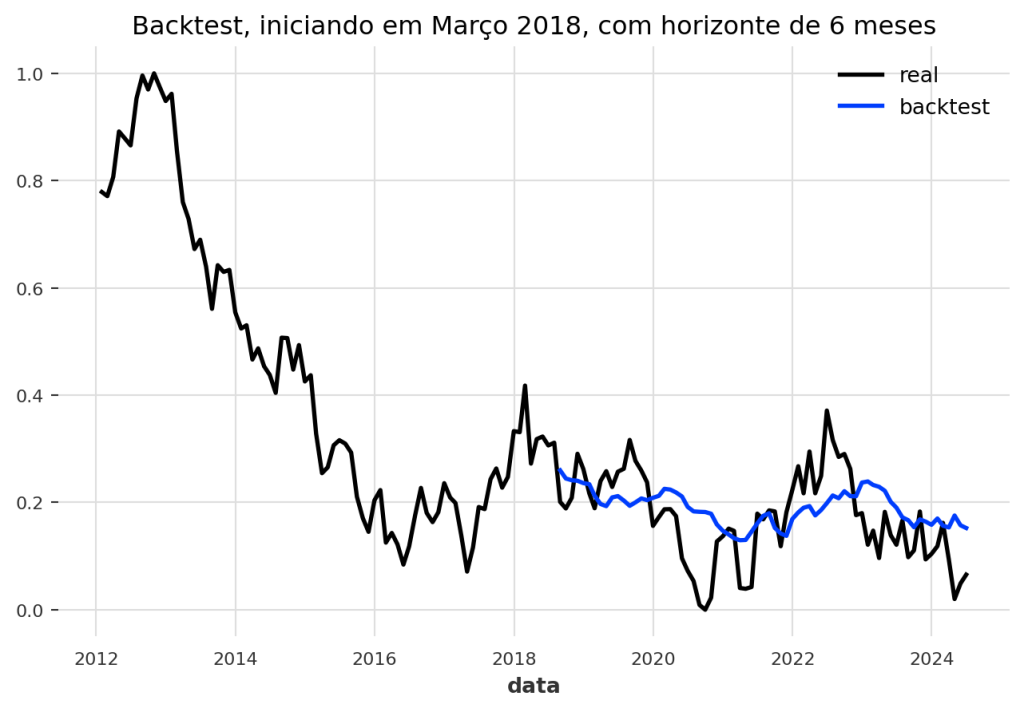
Teste Robusto com Backtesting
Uma forma ainda mais robusta de avaliar um modelo é através do backtesting. A ideia é simular o uso do modelo no passado. Ele faz uma previsão para alguns passos, avança no tempo, faz outra previsão, e assim por diante, em todo o conjunto de dados.
Vamos fazer um backtest do nosso modelo para avaliar seu desempenho com um horizonte de previsão de 6 meses.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
Finalmente, calculamos o erro (MAPE) do backtest. Note que precisamos reverter a normalização (inverse_transform) para que o erro seja calculado na escala original dos dados, tornando-o interpretável.
CÓDIGO DISPONÍVEL PARA MEMBROS DO CLUBE AM
MAPE: 11.02%Conclusão
Os Transformers representam uma mudança de paradigma na análise de séries temporais. Sua capacidade de capturar dependências complexas de longo prazo e a flexibilidade de sua arquitetura os tornam uma ferramenta indispensável para lidar com a complexidade dos dados do mundo real. Com o surgimento de bibliotecas acessíveis, a aplicação desses modelos poderosos está cada vez mais ao alcance de cientistas de dados e analistas financeiros.
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.
Referências
- AHMED, Sabeen; NIELSEN, Ian E.; TRIPATHI, Aakash; SIDDIQUI, Shamoon; RAMACHANDRAN, Ravi P.; RASOOL, Ghulam. Transformers in Time-Series Analysis: A Tutorial. Circuits, Systems, and Signal Processing, v. 42, n. 12, p. 7433-7466, 2023. Disponível em: https://researchwithrowan.com.
- ALAMMAR, Jay; GROOTENDORST, Maarten. Hands-On Large Language Models: Language Understanding and Generation. Sebastopol: O’Reilly Media, 2024.
- VASWANI, Ashish et al. Attention is All You Need. In: Advances in Neural Information Processing Systems (NIPS), 2017. Disponível em: https://deeprevision.github.io/posts/001-transformer.
- UNIT8 SA. Darts - Quickstart Guide. Disponível em: https://unit8co.github.io/darts/quickstart/00-quickstart.html#Export-a-TimeSeries