Juro Real vs. Juro Neutro

Nosso objetivo no Curso Mercado Financeiro e Gestão de Portfólios é o de proporcionar tanto uma introdução dos alunos ao mercado financeiro quanto o de munir os mesmos com ferramentas analíticas para gestão de portfólios e tratamento/visualização de dados. Para ilustrar, vamos ver como é possível construir o juro real e o juro neutro a partir de bases de dados disponíveis na internet e visualizar os mesmos com o pacote ggplot2 do R.

O juro real e o juro neutro têm importância fundamental para dizer a direção da política monetária operacionalizada pelo Banco Central. Em termos contemporâneos, inspirados no trabalho pioneiro de Knut Wicksell, dizemos que a política monetária é expansionista ou contracionista se, respectivamente, o juro real estiver abaixo ou acima da taxa de juros neutra. Taxa de juros neutra, por outro lado, é aquela consistente com a estabilidade da taxa de inflação ao longo do tempo. Variável não observável, que deve ser estimada e que depende de diversos fatores. Nesses termos, cabe ao Banco Central manter a taxa de juros real próxima à taxa de juros neutra, se o objetivo é controlar a inflação.

Pela equação de Fisher, sabemos que

(1)  

Onde, é a taxa de juros nominal, é a taxa de juros real e é a taxa de inflação. Rearranjando os termos, definimos o juro real ex-post como:

(2)  

Para tornar a análise ex-ante, devemos substituir pela expectativa de inflação, isto é, , de modo que o juro real ex-ante será dado por:

(3)  

Em outras palavras, o juro real ex-ante será dado, de forma aproximada, pela diferença entre o juro nominal e a expectativa de inflação. Essa é, em geral, a forma como o mercado calcula a taxa de juros real no país. Em termos exatos, o cálculo se dá pela fórmula:

(4)  

Na sequência, nós iremos construir o juro real e o juro neutro, com dados disponíveis na internet e colocar ambas as variáveis em um mesmo gráfico, de modo a visualizar a direção da política monetária sobre o ciclo econômico.

O script de R começa com alguns pacotes sendo carregados.

library(GetTDData)
library(readr)
library(xts)
library(forecast)
library(scales)
library(ggplot2)
library(mFilter)
library(grid)
library(png)
library(rbcb)
library(Quandl)

Na sequência, nós iremos pegar três séries: a taxa Selic, a expectativa de inflação e a taxa de juros associada à NTN-B 2050.

## Taxa de Juros
selic = Quandl('BCB/1178', order='asc', start_date='2012-06-01')

## Expectativa de Inflação 12 meses à frente
expinf = get_twelve_months_inflation_expectations('IPCA',
start_date = '2012-06-01')

## Taxa de Juros da NTN-B 2050
download.TD.data('NTN-B')
ntnb50 <- read.TD.files(dl.folder = 'TD Files',
maturity = '150850')

O juro real é então criado como abaixo.

selic = xts(selic$Value, order.by = selic$Date)
expinf12 = xts(expinf$mean[expinf$smoothed=='S'],
order.by = expinf$date[expinf$smoothed=='S'])
dataex = cbind(selic, expinf12)
dataex = dataex[complete.cases(dataex),]
juro_ex = (((1+(dataex[,1]/100))/(1+(dataex[,2]/100)))-1)*100

Na sequência, nós comparamos o juro real com o juro neutro extraído da taxa de juros associada à NTN-B.

juro_ntnb = xts(ntnb50$yield.bid*100, order.by = ntnb50$ref.date)
df = cbind(juro_ex, juro_ntnb)
df = df[complete.cases(df),]
df = data.frame(time=index(df), juroreal=df[,1],
ntnb=df[,2])

hp = hpfilter(df$juro_ntnb, fre=10000, type='lambda')
dftrend

Por fim, geramos um gráfico que compara as duas séries.

________________

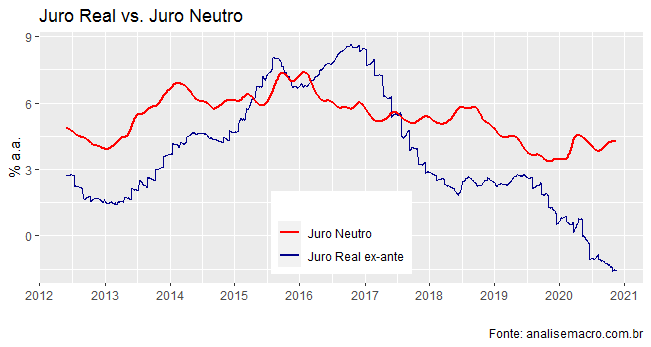
(*) Isso e muito mais você irá aprender no nosso Novo Curso Mercado Financeiro e Gestão de Portfólios.