Uma das medidas de risco mais populares no mundo das finanças está representado no Value at Risk, ou popularmente conhecido como VaR. O VaR mensura a perda em valor monetário de um portfólio em um determinado horizonte de tempo, com base em um intervalo de confiança. Dentre as diversas possibilidades de cálculo do VaR, que depende tanto da forma que se encontram os dados, quanto o objetivo a ser alcançado, iremos ensinar no post de hoje o método do VaR gaussiano.
O VaR gaussiano é uma da formas mais simples que existem para se calcular o risco da perda monetária de um portfólio, assumindo que a distrubuição dos retornos seja normal. Portanto, para calcular o VaR nesse tipo de medida, necessitamos apenas do intervalo de confiança, da média dos retornos e o desvio padrão dos retornos. Seguimos a seguinte equação:
(1)
onde é o nível de significância do VaR,
é média dos retornos,
é o desvio padrão,
é o z-score baseado no nível de significância do VaR e
é o atual valor monetário do portfólio.
Vamos então realizar os cálculos do VaR.
library(tidyverse) library(PerformanceAnalytics) library(timetk) library(quantmod)
Primeiro, iremos retirar os dados dos preços e calcular o retorno do portfólio, com base no peso de cada ativo.
# Define os ativos que irão ser coletados
tickers <- c("PETR4.SA", "ITUB4.SA", "ABEV3.SA", "JBSS3.SA")
# Define a data de início da coleta
start <- "2019-12-01"
# Realiza a coleta dos preços diários
prices <- getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
from = start,
src = "yahoo") %>%
map(~Cl(get(.))) %>%
reduce(merge) %>%
`colnames<-`(tickers)
# Calcula os retornos mensais
asset_returns <- Return.calculate(prices,
method = "log") %>%
na.omit()
# Define os pesos
w <- c(0.50, 0.27, 0.13, 0.10)
# Calcula o retorno do portfolio baseado no peso de cada ativo
portfolio_return <- Return.portfolio(asset_returns,
weights = w) %>%
`colnames<-`("port_returns")
# Calcula o retorno do portfolio com 1000 reais investidos
value <- cumprod(1 + portfolio_return) * 1000
Feito isso, podemos calcular o VaR. Devemos definir o valor monetário do nosso portfólio. Considerando que investimos 1000 reais no primeiro dia, sem aportar nenhum outro valor, temos que nosso portfólio até então chegou ao valor de 683,38 reais (podemos dizer que a montagem do portfólio não foi boa).
Em seguida, calculamos nosso VaR com base na média e no desvio padrão do portfólio. Utilizaremos dois níveis de significância para comparação: 1% e 5%.
# Calcula a média dos retornos port_mean <- mean(portfolio_return) # Calcula o desvio-padrão dos retornos port_risk <- sd(portfolio_return) # Calcula o Var gaussiano com 1% e 5% de significância var_01 <- -(port_mean + port_risk * qnorm(0.01)) var_05 <- -(port_mean + port_risk * qnorm(0.05)) # Calcula o valor monetário com base na significância value_01 <- round(last(value) * var_01) value_05 <- round(last(value) * var_05)
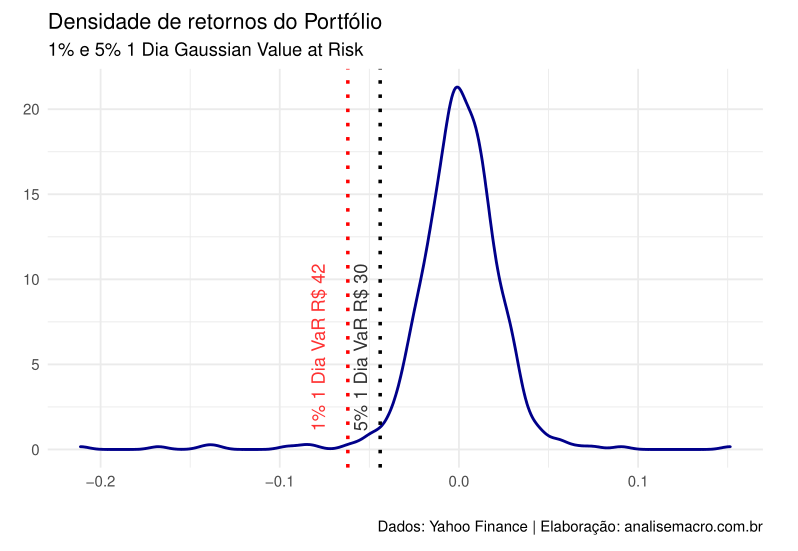
Por fim, podemos comparar em um gráfico nosso VaR.
# Transforma em tibble
portfolio_return_tbl <- portfolio_return %>%
tk_tbl(preserve_index = TRUE,
rename_index = "date")
# Plota o gráfico de densidade
ggplot(portfolio_return_tbl, aes(x = port_returns))+
geom_density(color = "darkblue",
size = .8)+
geom_vline(xintercept = -var_01,
linetype = "dotted",
color = "red",
size = 1)+
annotate(geom = "text",
x = -var_01,
y = 6,
label = paste("1% 1 Dia VaR", "R", value_01),
color = "red",
angle = 90,
alpha = .8,
vjust = -1.75)+
geom_vline(xintercept = -var_05,
linetype = "dotted",
color = "black",
size = 1)+
annotate(geom = "text",
x = -var_05,
y = 6,
label = paste("5% 1 Dia VaR", "R", value_05),
color = "black",
angle = 90,
alpha = .8,
vjust = -1)+
theme_minimal()+
labs(title = "Densidade de retornos do Portfólio",
subtitle = "1% e 5% 1 Dia Gaussian Value at Risk",
caption = "Dados: Yahoo Finance | Elaboração: analisemacro.com.br",
x = "",
y = "")
________________________
(*) Para entender mais sobre Mercado Financeiro e medidas de risco, confira nosso curso de R para o Mercado Financeiro.
________________________