{tidyverts} é uma família de pacotes de R criada para ser a próxima geração de ferramentas para modelagem e previsão de séries temporais, substituindo o famoso pacote {forecast}.
Utilizando uma interface simples e integrada com os pacotes do tidyverse, é possível construir uma ampla gama de modelos de previsão univariados e multivariados: ARIMA, VAR, suavização exponencial via espaço de estado (ETS), modelo linear (TSLM), autorregressivo (AR), passeio aleatório (RW), autoregressão de rede neural (NNETAR), Prophet, etc.
Neste exercício, daremos uma breve introdução aplicada a modelagem e previsão de séries temporais usando os pacotes do {tidyverts}.
Conhecendo os pacotes
Um breve resumo do que a família de pacotes do {tidyverts} tem a oferecer:
fable
- Coleção de modelos univariados e multivariados de previsão
- Modelagem de séries temporais em formato "tidy"
- Especificação de modelos utiliza terminologia de fórmula (y ~ x)
fabletools
- Extensões e ferramentas para construção de modelos
- Combinação de modelos, previsão hierárquica e extração de resultados
- Obtenção de medidas de acurácia e visualização de dados
feasts
- Decomposição de séries temporais
- Extração e visualização de componentes de séries temporais
- Análise de autocorrelação, testes de raiz unitária, etc.
tsibble
- Estrutura de dados tidy para séries temporais no R
- Funções para tratamento de dados
- Objeto orientado aos dados e a modelos, integrado ao tidyverse
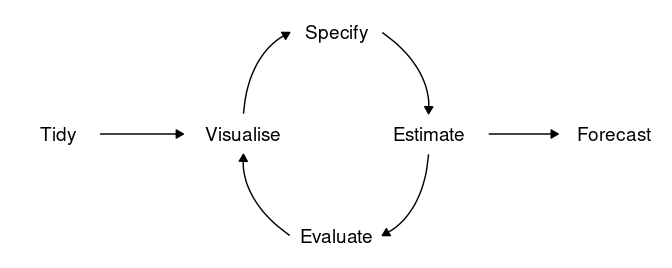
Fluxo de trabalho para previsão
Com o tidyverts o processo de construir um modelo de previsão pode ser dividido em poucos passos:
Com esse esquema em mente, vamos ilustrar esse processo com um exercício prático e didático: construir um modelo de previsão para a taxa de crescimento do PIB brasileiro.
Pacotes
Para reproduzir o exercício a seguir você precisará dos seguintes pacotes:
library(fable) # CRAN v0.3.1 library(fabletools) # CRAN v0.3.2 library(tsibble) # CRAN v1.1.1 library(tsibbledata) # CRAN v0.4.0 library(feasts) # CRAN v0.2.2 library(dplyr) # CRAN v1.0.7 library(tidyr) # CRAN v1.2.0 library(ggplot2) # CRAN v3.3.5
Dados tidy
Utilizaremos o dataset global_economy armazenado como um objeto tsibble, trazendo variáveis econômicas em frequência anual para diversos países. Nosso interesse é a série da taxa de crescimento do PIB brasileiro:
pib_br <- tsibbledata::global_economy %>% dplyr::filter(Country == "Brazil") %>% dplyr::select(Year, Growth) %>% tidyr::drop_na() pib_br # # A tsibble: 57 x 2 [1Y] # Year Growth # <dbl> <dbl> # 1 1961 10.3 # 2 1962 5.22 # 3 1963 0.875 # 4 1964 3.49 # 5 1965 3.05 # 6 1966 4.15 # 7 1967 4.92 # 8 1968 11.4 # 9 1969 9.74 # 10 1970 8.77 # # ... with 47 more rows
Visualização de dados
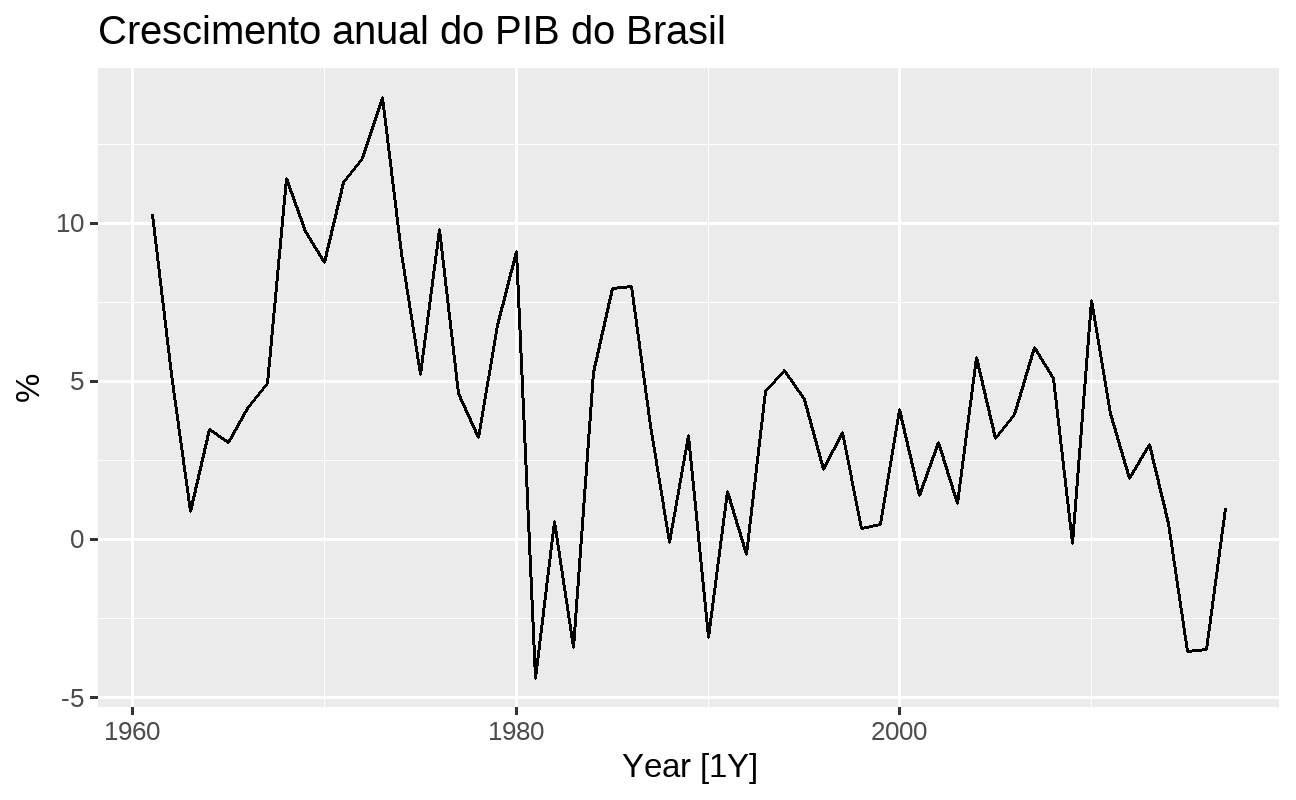
Visualização é uma etapa essencial para entender os dados, o que permite identificar padrões e modelos apropriados. No nosso exemplo, criamos um gráfico de linha para plotar a série do PIB brasileiro usando a função autoplot():
pib_br %>% fabletools::autoplot(Growth) + ggplot2::labs(title = "Crescimento anual do PIB do Brasil", y = "%")
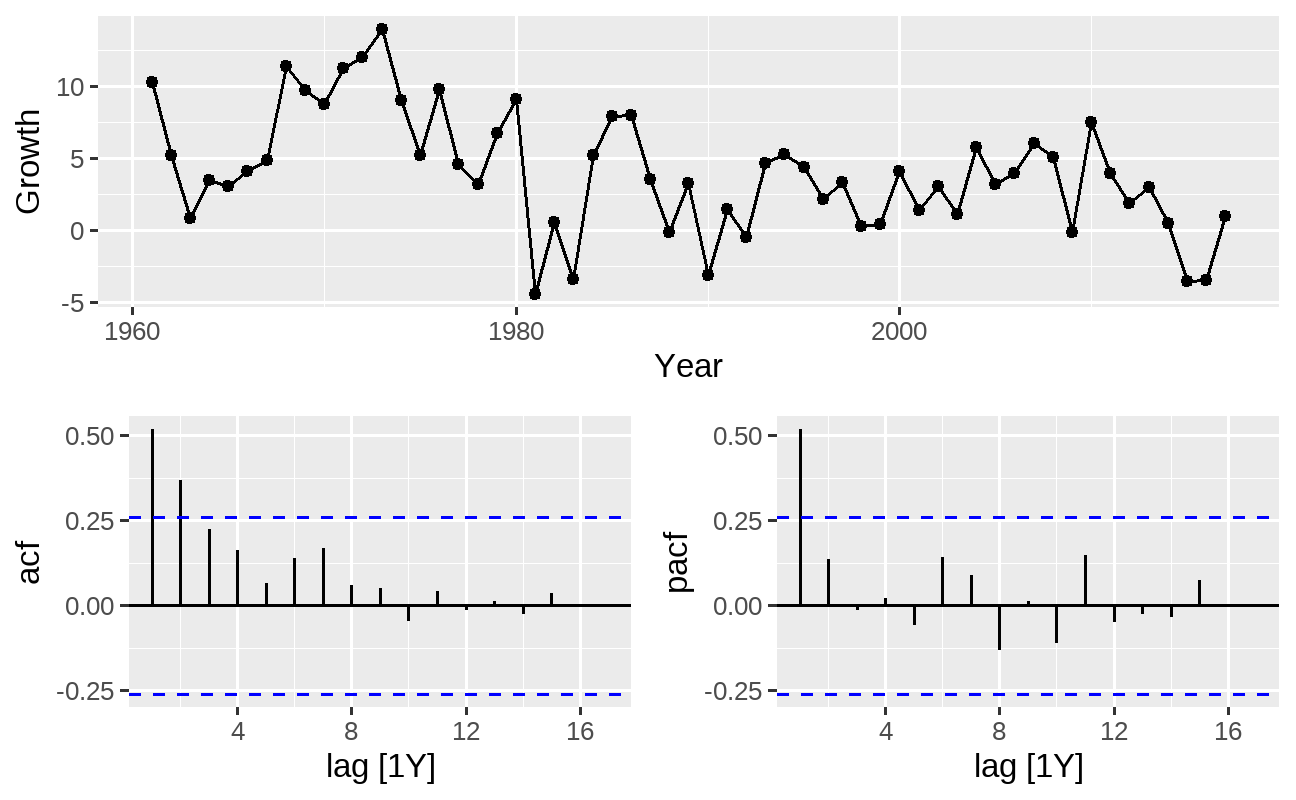
Podemos também plotar os correlogramas ACF e PACF para identificar o processo estocástico da série, obtendo alguns modelos candidatos:
pib_br %>% feasts::gg_tsdisplay(Growth, plot_type = "partial")
Especificação do modelo
Existem muitos modelos de séries temporais diferentes que podem ser usados para previsão, e especificar um modelo apropriado para os dados é essencial para produzir previsões.
Os modelos no framework do fable são especificados usando funções com nomenclatura abreviada do nome do modelo (por exemplo, ARIMA(), AR(), VAR(), etc.), cada uma usando uma interface de fórmula (y ~ x). As variáveis de resposta são especificadas à esquerda da fórmula e a estrutura do modelo é escrita à direita.
Por exemplo, um modelo ARIMA(1,0,2) para a taxa de crescimento do PIB pode ser especificado com: ARIMA(Growth ~ pdq(1, 0, 2)).
Neste caso, a variável resposta é Growth e está sendo modelada usando a estrutura de um modelo ARMA(1, 2) especificada na função especial pdq().
Existem diversas funções especiais para definir a estrutura do modelo e em ambos os lados da fórmula pode ser aplicado transformações. Consulte detalhes da documentação do fable.
Estimar o modelo
Identificado um modelo (ou mais) apropriado, podemos em seguida fazer a estimação usando a função model()1.Neste exemplo, estimaremos os seguintes modelos: ARIMA(1,0,2), ARIMA(1,0,0), ARIMA(0,0,2), o algoritmo de seleção automatizada do auto ARIMA criado pelo prof. Rob Hyndman e um passeio aleatório.
fit <- pib_br %>% fabletools::model( arima102 = fable::ARIMA(Growth ~ pdq(1, 0, 2)), arima100 = fable::ARIMA(Growth ~ pdq(1, 0, 0)), arima002 = fable::ARIMA(Growth ~ pdq(0, 0, 2)), auto_arima = fable::ARIMA(Growth), random_walk = fable::RW(Growth) )
Diagnóstico do modelo
O objeto resultante é uma "tabela de modelo" ou mable, com a saída de cada modelo em cada coluna:
fit # # A mable: 1 x 5 # arima102 arima100 arima002 # <model> <model> <model> # 1 <ARIMA(1,0,2) w/ mean> <ARIMA(1,0,0) w/ mean> <ARIMA(0,0,2) w/ mean> # # ... with 2 more variables: auto_arima <model>, random_walk <model>
Para obter os critérios de informação use a função glance():
fabletools::glance(fit) %>% dplyr::arrange(AICc) # # A tibble: 5 x 8 # .model sigma2 log_lik AIC AICc BIC ar_roots ma_roots # <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <list> <list> # 1 auto_arima 12.8 -150. 307. 307. 313. <cpl [1]> <cpl [1]> # 2 arima100 12.6 -152. 311. 311. 317. <cpl [1]> <cpl [0]> # 3 arima102 12.8 -152. 313. 314. 323. <cpl [1]> <cpl [2]> # 4 arima002 13.1 -153. 314. 315. 322. <cpl [0]> <cpl [2]> # 5 random_walk 16.0 NA NA NA NA <NULL> <NULL>
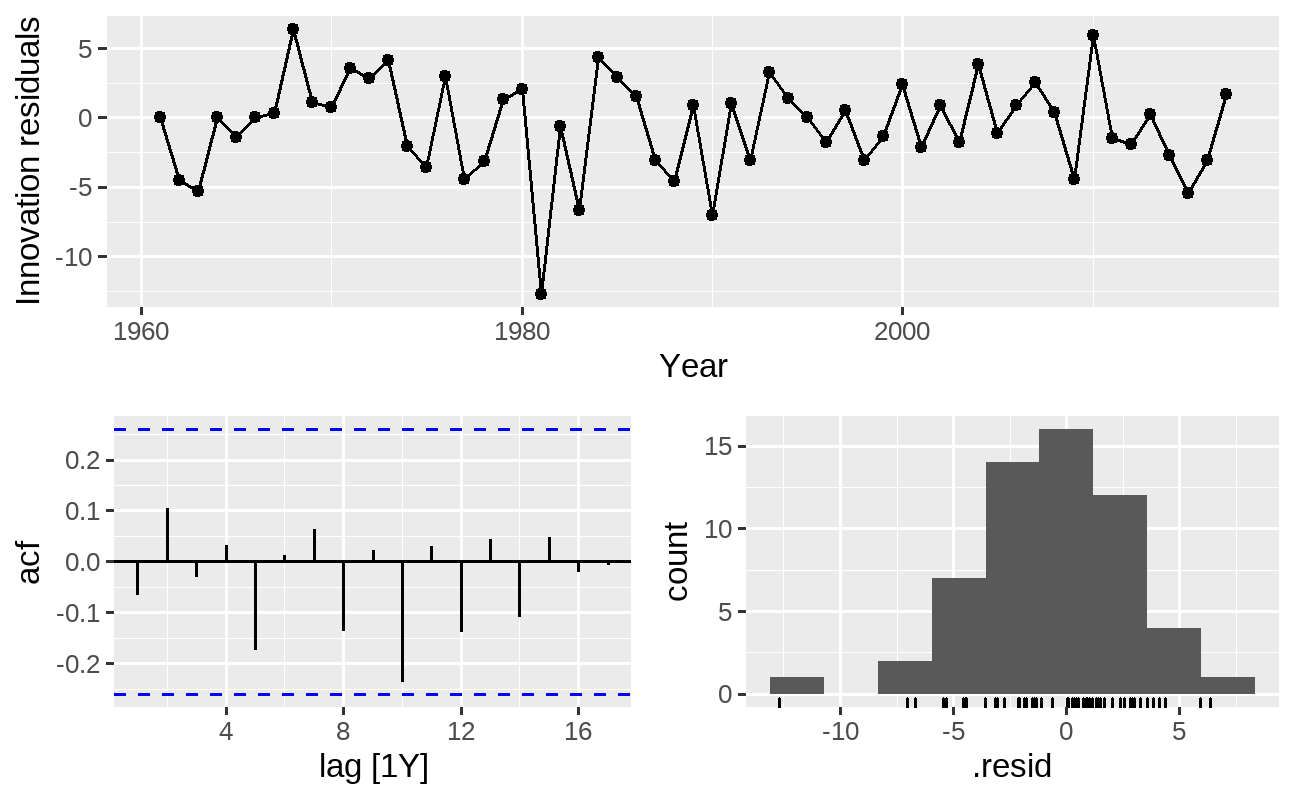
Os critérios de informação indicam que, dos modelos estimados, o modelo automatizado ARIMA(1,1,1) apresentou o menor valor de AICc - seguido pelos demais identificados pelos correlogramas ACF e PACF. Com a função gg_tsresiduals() podemos verificar o comportamento dos resíduos deste modelo, indicando que os resíduos se comportam como ruído branco:
fit %>% dplyr::select(auto_arima) %>% feasts::gg_tsresiduals()
Um teste de autocorrelação (Ljung Box) retorna um p-valor grande, também indicando que os resíduos são ruído branco:
fabletools::augment(fit) %>% dplyr::filter(.model == "auto_arima") %>% fabletools::features(.innov, feasts::ljung_box, lag = 10, dof = 3) # # A tibble: 1 x 3 # .model lb_stat lb_pvalue # <chr> <dbl> <dbl> # 1 auto_arima 8.63 0.281
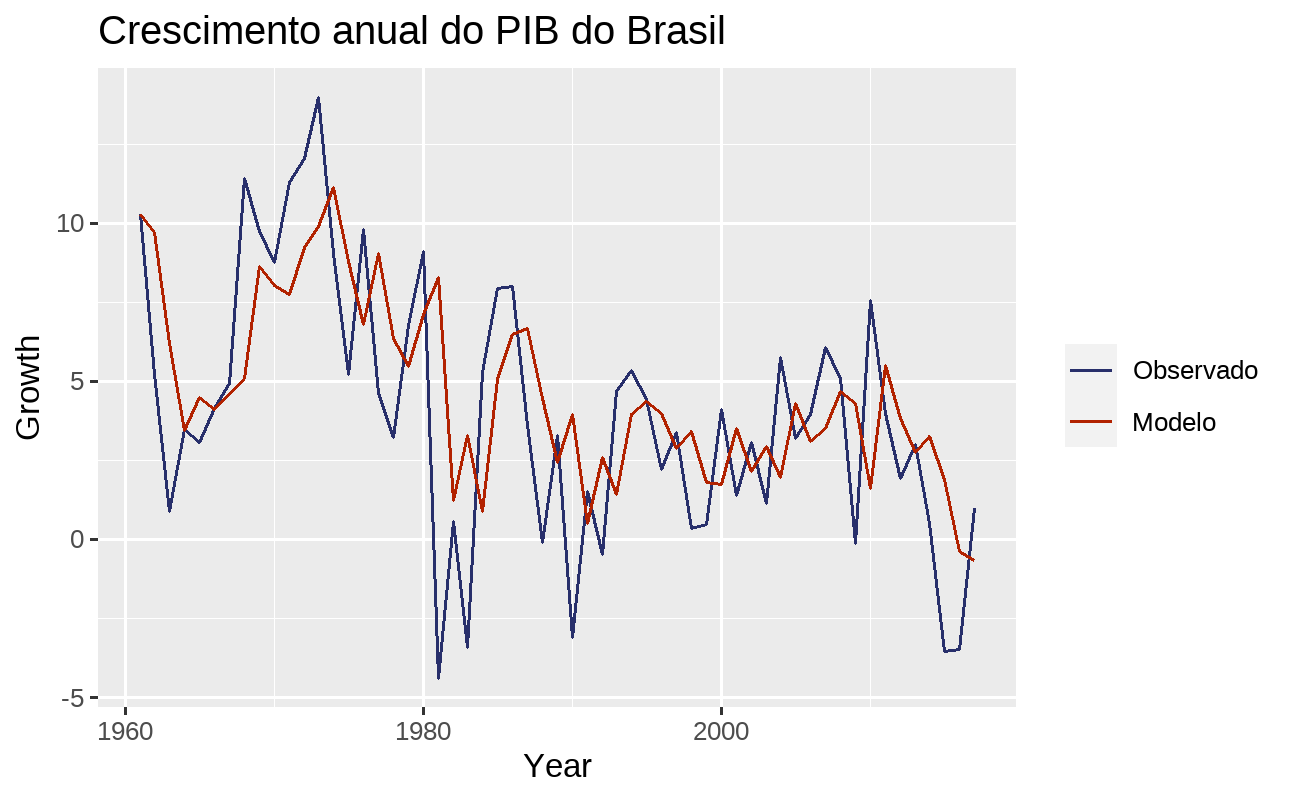
Também pode ser interessante visualizar o ajuste do modelo. Utilize a função augment() para obter os valores estimados:
fit %>% fabletools::augment() %>% dplyr::filter(.model == "auto_arima") %>% ggplot2::ggplot(ggplot2::aes(x = Year)) + ggplot2::geom_line(ggplot2::aes(y = Growth, colour = "Observado")) + ggplot2::geom_line(ggplot2::aes(y = .fitted, colour = "Modelo")) + ggplot2::scale_colour_manual( values = c(Observado = "#282f6b", Modelo = "#b22200") ) + ggplot2::labs(title = "Crescimento anual do PIB do Brasil", colour = NULL)
Previsão
Com o modelo escolhido, previsões podem ser geradas com a função forecast() indicando um horizonte de escolha.
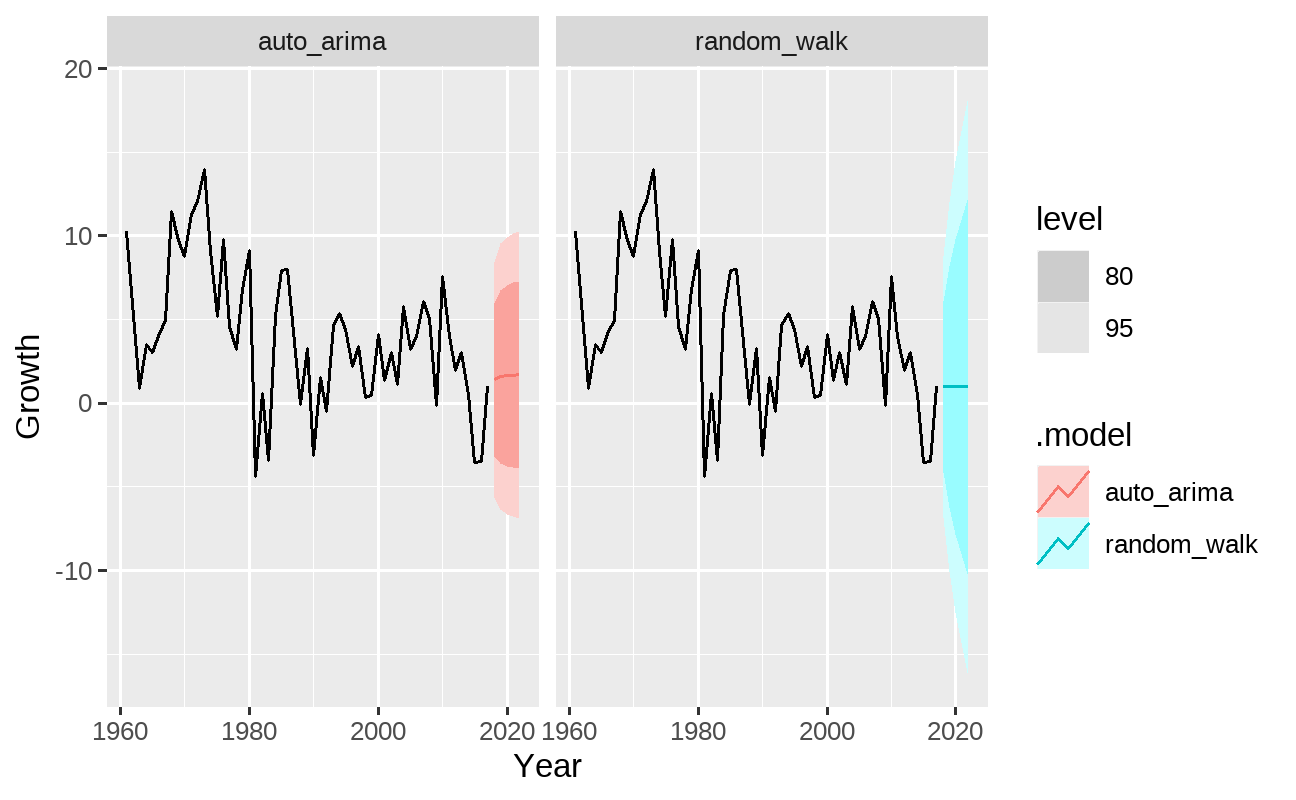
fit %>% dplyr::select(auto_arima, random_walk) %>% fabletools::forecast(h = 5) %>% fabletools::autoplot(pib_br) + ggplot2::facet_wrap(~.model)
Perceba que os pontos de previsão médios gerados são bastante similares a um processo de passeio aleatório (equivalente a um ARIMA(0,1,0)). O trabalho adicional de especificar termos AR e MA trouxe pouca diferença para os pontos de previsão neste exemplo, apesar de ser perceptível que os intervalos de confiança do modelo auto ARIMA são mais estreitos do que de um passeio aleatório.
Além disso, a previsão fora da amostra gerada ficou bastante aquém dos dados reais para a taxa de crescimento do PIB brasileiro observados no horizonte em questão, configurando apenas um exercício didático.
Saiba mais
Estes são apenas alguns dos recursos e ferramentas disponíveis na família de pacotes do tidyverts. Para uma referência aprofundada, confira o livro Forecasting: Principles and Practice, 3rd Edition, de Hyndman e Athanasopoulos (2021).
Confira outros exercícios aplicados com pacotes do tidyverts:
- Gerando previsões desagregadas de séries temporais
- Como extrair componentes de tendência e sazonalidade de uma série temporal
- Como estimar modelos para múltiplas séries temporais ao mesmo tempo
[1] A função suporta estimação dos modelos com computação paralela usando o pacote future, veja detalhes na documentação e este post para saber mais sobre o tema.