Em uma conversa econômica essa semana com um amigo não economista de longa data, surgiu o assunto do "viés do mercado". Ele tinha a impressão que as expectativas colhidas pelo Banco Central junto a instituições do mercado financeiro seriam viesadas. Ou seja, tenderiam a refletir um comportamento pré-estabelecido, baseado em suas preferências por juros altos, por exemplo. Será? Como trabalho com esse banco de dados há algum tempo, acabei respondendo para esse meu amigo o que penso a respeito. Dado que pode ser uma dúvida de outras pessoas, proponho nesse post um exercício simples para tentarmos entender melhor esse problema.
Um jeito realmente muito simples de ver isso é pegar a diferença entre a expectativa e a realização de alguma variável e verificar se essa série tem mais observações positivas ou negativas. No primeiro caso, a expectativa é sistematicamente maior do que a realização, o que, no caso dos juros, daria evidência empírica para o argumento do meu amigo. Você pode fazer isso para os juros, mas como vivemos [ou vivíamos] em um regime de metas, acho que faz mais sentido verificar valor esperado e efetivo da inflação.
Sem entrar em maiores detalhes, a ideia é realmente muito simples: se o "mercado" quer mais juros, ele deve superestimar a inflação. Afinal, expectativas de inflação maiores exigem mais juros por parte do Banco Central para que a inflação efetiva convirja. É isso que ocorre?
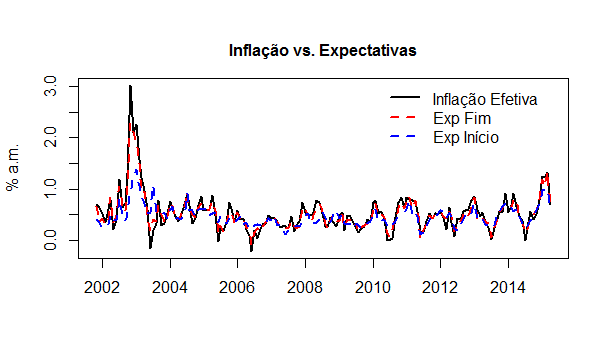
Eu peguei três séries, de novembro de 2001 a abril de 2015: a expectativa no primeiro e no último dia útil de cada mês e a inflação mensal medida pelo IPCA. O gráfico com as séries é posto abaixo.
Pelo gráfico é possível verificar que a expectativa no último dia útil é mais aderente à inflação efetiva do que a do primeiro dia útil. A correlação é mais forte entre a expectativa no último dia útil e a inflação efetiva, como pode ser visto abaixo.
| inflacao | expfim | expinicio | |
| inflacao | 1 | 0,96 | 0,75 |
| expfim | 0,96 | 1 | 0,85 |
| expinicio | 0,75 | 0,85 | 1 |
A partir dessas séries, montei duas outras, ao fazer a diferença entre expectativa e inflação efetiva. Assim, tenho o desvio para o primeiro e o último dia útil de cada mês. Feito isto, podemos regredir o desvio contra uma constante, de forma a ver o sinal do coeficiente que indica a média do erro que os agentes cometem. O código dessa regressão simples é colocada abaixo.
################# REGRESSÃO ################## inicio <- lm(desvio.inicio~1) summary(inicio) fim <- lm(desvio.fim~1) summary(fim)
Uma tabela com as regressões é posta abaixo.
| Dependent variable: | ||
| desvio.inicio | desvio.fim | |
| (1) | (2) | |
| Constant | -0.067*** | -0.021** |
| (0.022) | (0.009) | |
| Observations | 162 | 162 |
| R2 | 0.000 | 0.000 |
| Adjusted R2 | 0.000 | 0.000 |
| Residual Std. Error (df = 161) | 0.276 | 0.119 |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | |
Pois é. O sinal de ambos os coeficientes é negativo, o que indica que em média os agentes subestimam a inflação. Repare, também, que o coeficiente do desvio.fim é menor do que o do desvio.inicio, o que indica que no último dia útil o erro dos agentes é menor do que no primeiro. Mas ainda assim, é uma expectativa subestimada da inflação efetiva. E, de novo, estou pegando a expectativa no primeiro e no último dia útil para o mês t e confrontando com a inflação do mês t.
Como disse para o meu amigo, as expectativas dos agentes malvados do mercado financeiro são, de fato, viesadas: mas para baixo! Eles esperam em média uma inflação menor do que ela é no fim das contas. Explicação para isso? A minha preferida é que o Brasil é um país sujeito a muitos choques [inclusive, de política econômica], o que acaba por gerar uma inflação sistematicamente maior do que o esperado.
Pois é, leitor, antes de usar alguma teoria de conspiração é sempre bom consultar os dados, não? 🙂