No Hackeando o R de hoje, vamos mostrar como realizar a estimação de um modelo linear misto. O método deriva seu nome devido à possibilidade de um modelo apresentar tanto efeitos fixos como aleatórios, porém é bom fazer um aviso: a nomenclatura utilizada nesse modelo é proveniente da bioestatística, que chama de efeitos fixos aqueles que são invariantes na população, e efeitos aleatórios aqueles que possuem uma distribuição de probabilidade que assume um valor para cada indivíduo.
Para compreender essas definições, vamos utilizar um exemplo do pacote lme4. Abaixo, fazemos uma regressão simples sobre os dados do dataset sleepstudy. Ele é proveniente de um estudo onde indivíduos foram restritos a 3 horas de sono por noite, e a cada dia seu tempo de reação foi observado.
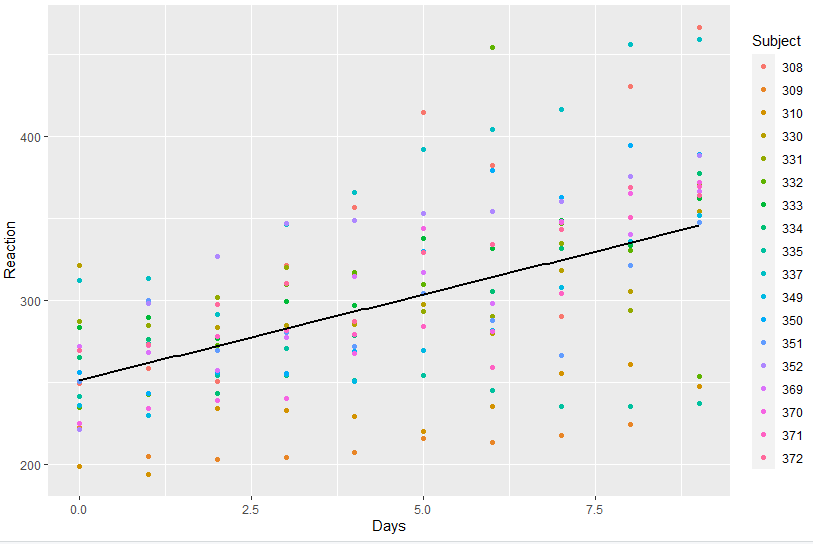
library(lme4) library(ggplot2) ggplot(sleepstudy, aes(Days, Reaction, colour = Subject)) + geom_point() + geom_smooth(method = "lm", colour = "black", se = FALSE)
Como podemos ver, há indivíduos que se mantém consistentemente abaixo da reta de regressão, pois devem possuir tempo de reação menor de modo generalizado, enquanto há outros que estão sempre acima. Isso reflete o fato de que a amostra não possui observações independentes (pois é feita para cada indivíduo ao longo de 10 dias), e não podemos utilizar o modelo linear clássico. A solução oferecida por um modelo linear misto é gerar um componente aleatório que é específico a cada indivíduo, de modo que podemos ter, para cada um, um intercepto e uma inclinação distintas. Para fazer isso, basta utilizar a função lmer:
m4 <- lmer(Reaction ~ Days + (1|Subject) + (0 + Days|Subject), data = sleepstudy) summary(m4, correlation = FALSE) Linear mixed model fit by REML ['lmerMod'] Formula: Reaction ~ Days + (1 | Subject) + (0 + Days | Subject) Data: sleepstudy REML criterion at convergence: 1743.7 Scaled residuals: Min 1Q Median 3Q Max -3.9626 -0.4625 0.0204 0.4653 5.1860 Random effects: Groups Name Variance Std.Dev. Subject (Intercept) 627.57 25.051 Subject.1 Days 35.86 5.988 Residual 653.58 25.565 Number of obs: 180, groups: Subject, 18 Fixed effects: Estimate Std. Error t value (Intercept) 251.405 6.885 36.513 Days 10.467 1.560 6.712
O modelo acima possui tanto intercepto e inclinação populacionais, como também coeficientes correspondentes para cada um dos indivíduos. No formato acima, supomos que os coeficientes individuais não são correlacionados (note que são escritos separadamente), o que pode ser testado, porém está fora do escopo do post de hoje. A partir desse modelo, podemos visualizar as retas de regressão, e compará-las com a reta que seria estimada ao fazer uma regressão para cada indivíduo:
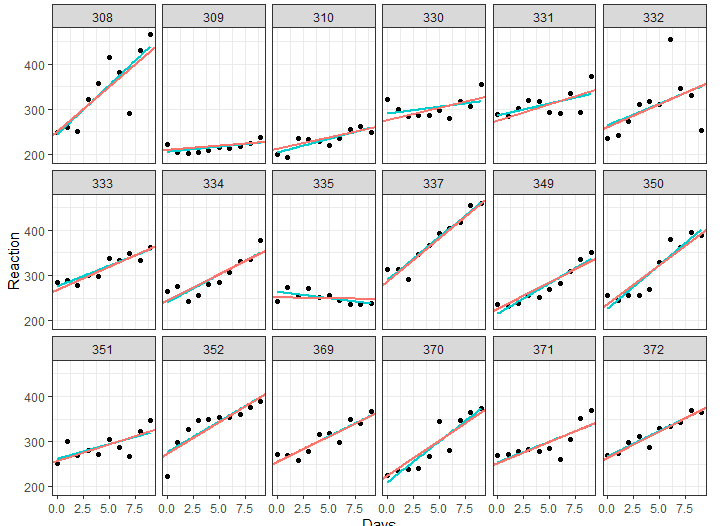
mixed_mod <- coef(m4)$Subject mixed_mod$Subject <- row.names(mixed_mod) ggplot(sleepstudy, aes(Days, Reaction)) + geom_point() + theme(legend.position = "none") + facet_wrap(~ Subject, nrow = 3) + geom_smooth(method = "lm", colour = "cyan3", se = FALSE, size = 0.8) + geom_abline(aes(intercept = `(Intercept)`, slope = Days, color = "magenta"), data = mixed_mod, size = 0.8) + theme_bw()
Como podemos ver, as retas são diferentes (sendo a azul a regressão OLS), o que ocorre pois as regressões do modelo misto são aproximadas em direção à média de todas elas.
________________________
(*) Para entender mais sobre estimação de modelos e regressão, confira nossos Cursos de Econometria e Machine Learning.