É extremamente difícil obter dados para uma população inteira, desta forma, ao realizar uma análise de dados, devemos utilizar métodos para generalizar os resultados de uma amostra para uma população, e podemos atingir o objetivo utilizando a inferência estatística. No post de hoje, elencamos o processo de inferência estatística e como podemos aplicar utilizando um exemplo com o R.
Com o objetivo de estimar os parâmetros de uma análise de dados de uma amostra para uma população, devemos ter em mãos ferramentas que possibilitam alcançar este objetivo. Através dos conhecimentos obtidos através de um rigor crítico, da AED e dos conceitos de probabilidade, conseguimos realizar uma análise dos dados. Mas como agir nos passos seguintes para saber se uma amostra é significativa? Para isso utilizamos a inferência estatística e o método de testes de hipóteses.
Mas afinal, o que é inferência? Como devemos seguir os passos para generalizar os resultados de uma amostra para uma população? A inferência estatística segue uma estrutura que provê passos para que possamos ser bem sucedidos no processo:
- Coletar uma amostra representativa: É necessário realizar este procedimento antes do teste de hipóteses (que iremos explicar adiante), pois é crucial para o sucesso dos passos seguintes. Devemos ter certeza que a amostra coletada é representativa da população, senão, incorremos de um viés estatístico. Este processo de certeza é realizado durante a fase de coleta, no qual deve ser bem definido todos os processos.
- Crie as hipóteses: Devemos criar a motivação do trabalho e confeccionar uma hipótese, que pode ser criada das seguintes formas: afirmar ou contrapor um senso comum; testar alguma teoria criada pela literatura; certificar o comportamento do objeto analisado; e entre outras formas.
- Formular um plano de analise: será o ferramental utilizado para conduzir o teste, ou seja, os métodos estatísticos utilizados para mensurar a amostra, realizar o teste e a avaliação.
- Analisar os dados: De fato, estará sendo feito a analisar dos dados, de forma a obter um insight prévio sobre como conduzir os testes. Construir as estatísticas descritivas, e construir visualizações para entender a distribuição dos dados é crucial. Realiza os testes
- Faça uma decisão: com base nos resultados da análise, iremos avaliar se o plano construído foi alcançado, sendo avaliado as hipóteses. Aqui será crucial conhecimento da significância estatísticas.
Inferência no R
Como exemplo, utilizaremos o dataset Housing, oriundo do pacote Ecdat, que fornece o preços de casas a vendas na cidade de Windsor. Com base nestes dados, seguiremos os passos elencados acima para obter um ideia de como podemos entender a inferência estatística.
Amostra Representativa
Obviamente, seria dificultoso capturar os preços de todas as casas da cidade de Windsor, entretanto, mesmo com este problema, a amostra deve ser suficientemente grande o bastante para retirar quaisquer conclusões. Com 546 observações, sabemos que pode ser útil para a realização de uma inferência.
Apesar do tamanho, não sabemos como foi realizado a pesquisa, e portanto, não podemos ter certeza se há algum viés na coleta ou se houve algum problema na coleta de dados, entretanto, são dados oriundos do Journal of Applied Econometrics, o que nos leva a crer que há autoridade e confiabilidade sobre os dados.
Criar as Hipóteses
Ao tentar entender como é formado os preços das casas, podemos entender inúmeras variáveis, desde o tamanho da casa, a arquitetura, sua localização e entre diversas outras. Para formular uma hipótese sobre o que pode afetar o preço de uma casa, devemos divagar sobre todas estas variáveis. Dentro da amostra, veja que há variável airco, que relata se a casa observada possui ar condicionado ou não. Bem, é lógico pensar: é difícil encontrar alguém que não goste de usufruir de um air condicionado, aumenta o bem estar das pessoas, logo, entendemos que para que haja esse aumento de bem estar, os indivíduos paguem mais pela casa, certo?
Para saber se esse pensamento é válido, podemos criar hipóteses estatística que podem nos auxiliar a provar essa relação.
H0: não há diferença no preço médio das casas a vendas com ou sem ar condicionado
H1: há diferença no preço médio das casas a vendas com ou sem ar condicionado
Como dito, essas hipóteses são mutuamente exclusivas, ou seja, se uma é verdadeira a outra necessita ser falsa.
Formular um plano de análise
Devemos agora definir os métodos que usaremos para analisar as hipóteses criadas. O ferramental da estatística é grande, logo devemos sempre realizar uma análise sobre os dados antes de partir para os testes de fato. Acima, ao analisar o data frame, vimos que o preço das casas vendidas é definido por uma variável continua e a variável airco é um factor, representando uma variável categórica binária. Também formulamos que o fato de uma casa ter ou não ar condicionado afeta o seu preço, logo, entendemos que o price é uma variável dependente e airco é uma variável independente.
Para entender esse relacionamento, utilizaremos o teste t para amostras independentes, que irá assumir que as observações são independentes e que a amostra segue distribuição normal.
Como temos incerteza sobre o resultado da amostra em relação a população, devemos definir como podemos alcançar a significância estatística do teste. Isto é, como na probabilidade, podemos quantificar essa incerteza, portanto, definimos um número de forma a obter a certeza do efeito média de uma variável em relação a outra, convencionalmente (e aqui utilizando teste bicaudal) utiliza-se 5%.
Analisar os dados
Podemos enfim realizar análise dos dados pensando crucialmente nas hipóteses definidas. A realização da análise pode ser um dos primeiros passos, de forma a ser familiarizar com os dados e obter insights, entretanto, para obtermos respostas sobre alguma hipótese, devemos faze-lo depois que é realizado todos os passos anteriores.
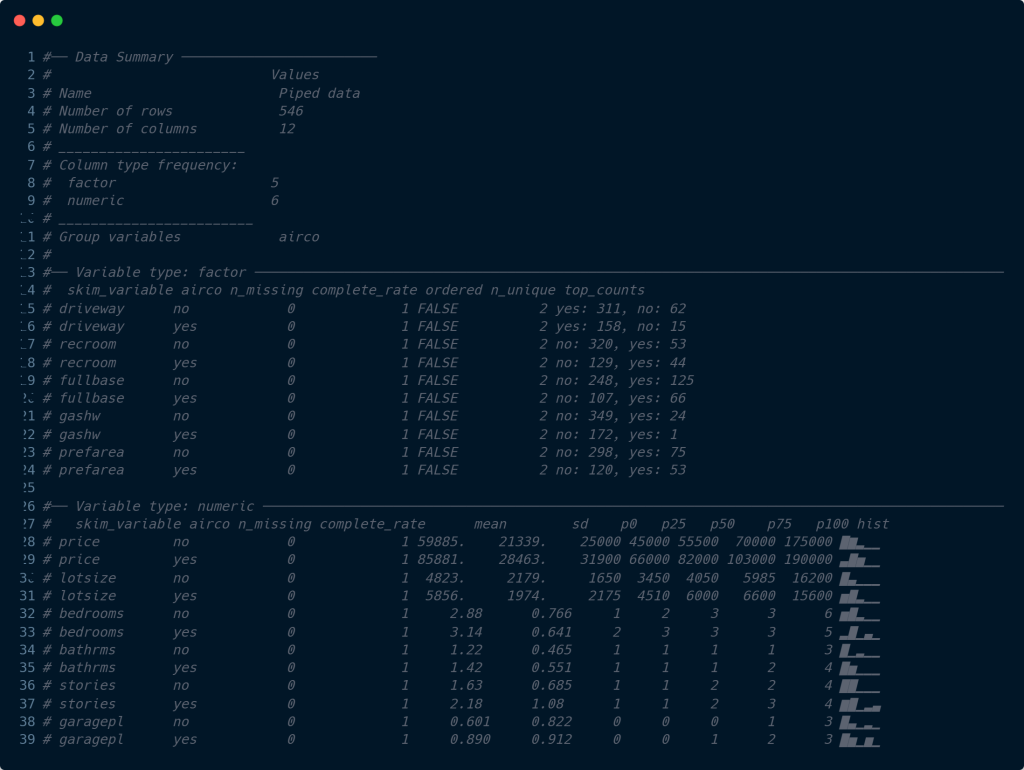
Para analisar os dados, utilizamos o pacote {skimr}, que irá calcular as estatísticas descritivas do dataset, veja que agrupamos pela variável airco, de forma que possamos obter os resultados separados por suas categorias.
Temos então uma ideia de como ser comporta o efeito de airco sobre price. As casas que possuem ar condicionado possuem um preço médio maior que as que não possuem, bem como possuem uma variabilidade menor.
Como o teste t presume que os dados sejam normais, podemos ver a distribuição para que possamos realizar o teste.
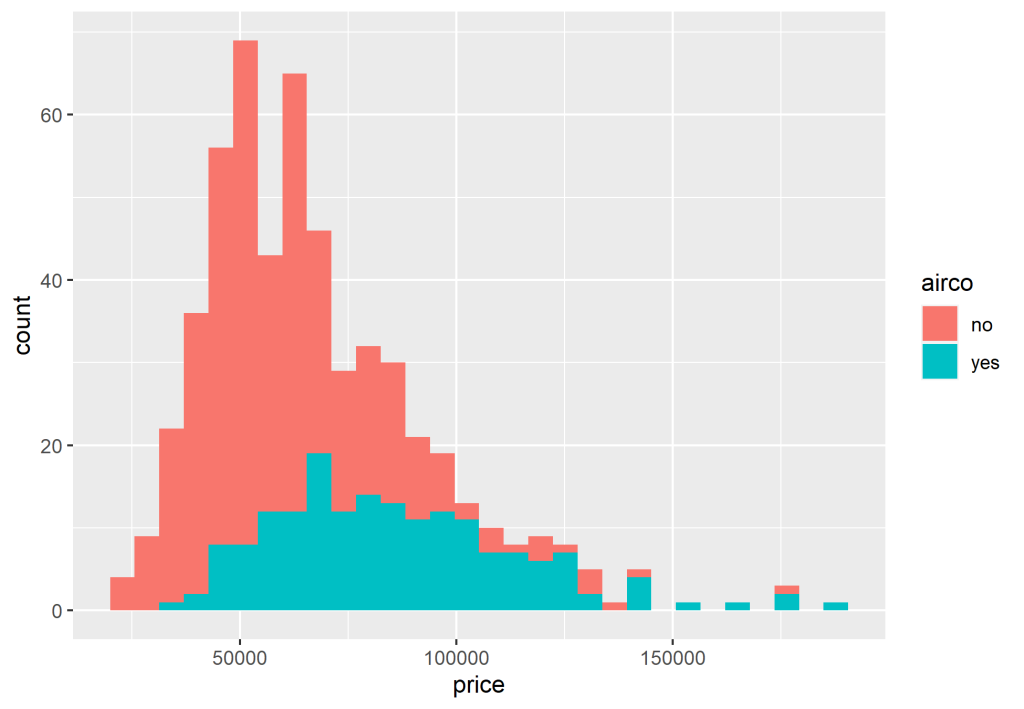
Por fim, conduzimos o teste t utilizando a função t.test(). Abaixo, nos resultados, vemos que com um nível de significância (95% porcento de confiança) de 5%, que o efeito é significativo, pois o p-valor da estatística é menor de 0.05, ou seja, rejeitamos H0 e aceitamos H1.
Podemos afirmar também que, com significância, que casas com ar condicionado possuem uma diferença negativa de aproximadamente $ 26000,00 em relação a casas com ar condicionado.
____________________________________________
Quer saber mais?
Veja nossos cursos de R e Python aplicados para a Análise de Dados e Economia
- R para Análise de Dados
- Python para Análise de Dados
- Gráficos com ggplot2
- Estatística usando R e Python
- Machine Learning usando o R
_____________________________________________
Referências
Mount, G. Advancing Into Analytics. Estados Unidos, O'Reilly Media, 2021.