Por que previsão é importante?
A capacidade de prever eventos futuros é uma necessidade crítica em muitas áreas, especialmente em economia e finanças. A previsão é importante porque ajuda a tomar decisões mais informadas e embasadas em dados. Por exemplo, uma empresa pode usar previsões para planejar a produção e gerenciar estoques, enquanto um investidor pode usar previsões para tomar decisões informadas sobre investimentos.
Através da previsão, é possível antecipar tendências, identificar padrões, estimar riscos e oportunidades, e assim tomar decisões mais acertadas e eficazes. Além disso, a previsão permite que as organizações se preparem para o futuro, planejem seus investimentos e recursos de maneira mais eficiente e, assim, aumentem sua competitividade. Em resumo, a previsão é importante porque ajuda a reduzir a incerteza e a maximizar as chances de sucesso em diferentes áreas e setores.
Profissão e salários
O cientista de dados é uma das profissões mais promissoras do mercado atual e tem como atribuição, em geral, o desenvolvimento de modelos de previsão. Com a explosão do uso de dados em todos os setores, os profissionais que sabem extrair informações valiosas de grandes volumes de dados se tornaram extremamente valorizados. Na área de economia e finanças, um cientista de dados que trabalha com previsão de séries temporais pode ajudar a identificar tendências e padrões, avaliar riscos, prever comportamentos de mercado, entre outras análises relevantes para a tomada de decisão.
Em relação ao salário, o cientista de dados que trabalha com previsão de séries temporais na área de economia e finanças pode esperar uma remuneração atraente, especialmente se possuir experiência e qualificações adequadas. Segundo dados do site Glassdoor, um Cientista de Dados Júnior pode ganhar em média de R$ 3.000 a R$ 7.000 por mês no Brasil. No entanto, é importante destacar que esses valores podem variar bastante dependendo da empresa, do nível de experiência, da região geográfica, entre outros fatores. É uma profissão desafiadora, mas também altamente gratificante e recompensadora em termos financeiros.
O que são séries temporais?
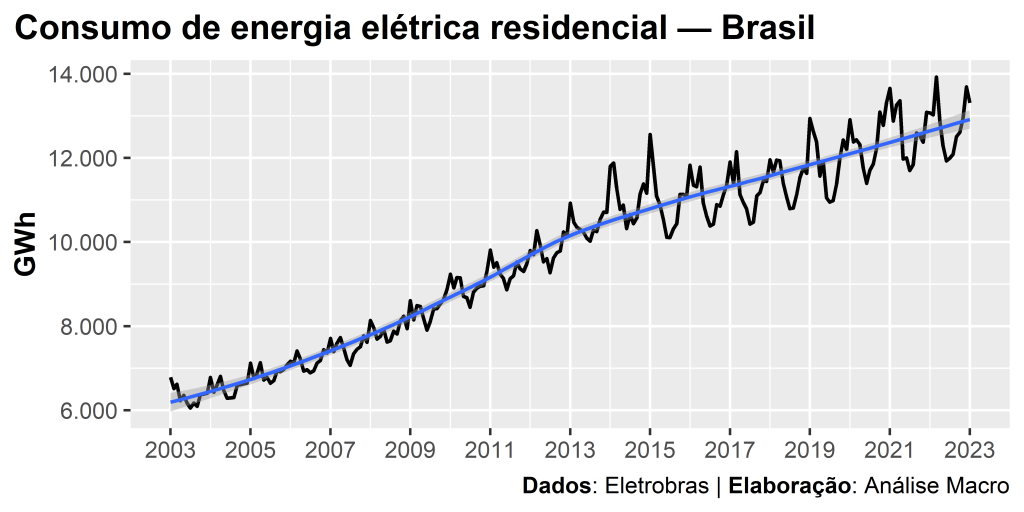
Séries temporais são conjuntos de dados que representam a evolução de uma variável ao longo do tempo, ou seja, são sequências de observações em ordem cronológica. São principalmente utilizadas em análises que buscam identificar padrões e tendências em dados históricos, a fim de fazer previsões sobre eventos futuros. As séries temporais são compostas por observações em um determinado intervalo de tempo, como dias, meses, trimestres, anos, entre outros. As séries temporais estão presentes em muitas áreas do nosso cotidiano, incluindo economia, finanças, clima, demografia e engenharia.
Na área de economia e finanças, as séries temporais são amplamente utilizadas para prever comportamentos e movimentações no mercado financeiro. Por exemplo, o histórico de preços de uma ação em bolsa de valores pode ser utilizado para prever seu valor futuro. Outro exemplo é a utilização de séries temporais para prever taxas de inflação, taxas de juros, variação cambial, entre outras variáveis econômicas relevantes. As séries temporais também são usadas para identificar ciclos econômicos e tendências de longo prazo em indicadores econômicos, o que pode ajudar na tomada de decisões de investimento e planejamento estratégico.
Quais são os componentes de uma série temporal?
Os componentes de uma série temporal são as diferentes fontes de variação que influenciam o comportamento da variável ao longo do tempo. Existem quatro componentes principais em uma série temporal: tendência, sazonalidade, ciclo e ruído.
- Tendência: é a mudança gradual ao longo do tempo, que reflete o comportamento de longo prazo da variável. Pode ser crescente, decrescente ou estável.
- Sazonalidade: é a variação periódica e fixa da série temporal, que se repete em intervalos regulares, como diário, semanal, mensal ou anual. Pode ser influenciada por fatores climáticos, sazonais ou de mercado, como as vendas de Natal.
- Ciclo: é uma variação de médio prazo na série temporal, que se repete em intervalos irregulares. Geralmente é causado por fatores econômicos, políticos ou sociais, como recessões ou expansões econômicas.
- Ruído: o ruído ou erro é a variação aleatória que não pode ser explicada pelos outros componentes. É uma fonte de incerteza e imprevisibilidade na série temporal.
Técnicas de previsão de séries temporais
Existem diversas técnicas de previsão de séries temporais que podem ser aplicadas em economia e finanças, cada uma com suas vantagens e limitações. Alguns dos métodos mais comuns incluem:
- Métodos estatísticos: esses métodos buscam estabelecer um modelo matemático que represente o comportamento da série temporal ao longo do tempo. As técnicas estatísticas mais comuns incluem a análise de médias móveis, análise de séries temporais univariadas, modelos ARIMA (Autoregressive Integrated Moving Average), modelos SARIMA (Seasonal ARIMA) e modelos de suavização exponencial.
- Métodos econométricos: os métodos econométricos buscam modelar a relação entre variáveis econômicas e financeiras, usando dados históricos para prever o comportamento futuro. Essas técnicas incluem regressão linear, modelos VAR (Vector Autoregression), modelos VEC (Vector Error Correction), modelos ARCH (Autoregressive Conditional Heteroscedasticity) e modelos GARCH (Generalized Autoregressive Conditional Heteroscedasticity).
- Métodos de machine learning: esses métodos utilizam algoritmos de aprendizado de máquina para extrair padrões e tendências da série temporal, a fim de produzir previsões. As técnicas de machine learning mais comuns incluem árvores de decisão, redes neurais, modelos de regressão não-linear, dentre outros.
Cada técnica tem suas vantagens e limitações, e a escolha da melhor técnica dependerá do problema específico que se pretende resolver, dos dados disponíveis e do contexto em que a previsão está sendo realizada. É importante ressaltar que a análise cuidadosa dos dados é fundamental para garantir a qualidade das previsões, independentemente da técnica escolhida.
Ferramentas para trabalhar com previsão
Aprender linguagens de programação como R e Python é importante para previsão de séries temporais por diversas razões. Primeiramente, essas linguagens são amplamente utilizadas por cientistas de dados e pesquisadores em diversas áreas, incluindo economia e finanças, o que significa que há uma grande comunidade de usuários e um vasto conjunto de bibliotecas e recursos disponíveis para realizar análises sofisticadas.
Além disso, R e Python são linguagens de programação de código aberto, o que significa que são gratuitas e altamente personalizáveis. Isso permite que os usuários criem ferramentas e pacotes personalizados para atender às necessidades específicas de suas análises e modelagem.
Outra vantagem dessas ferramentas é a capacidade de lidar com grandes quantidades de dados, o que é especialmente importante em séries temporais de alta frequência ou em análises que envolvem várias séries temporais simultaneamente.
Por fim, as linguagens R e Python possuem uma grande variedade de bibliotecas e pacotes que facilitam a implementação de técnicas de previsão de séries temporais. Por exemplo, o pacote "forecast" do R fornece uma ampla gama de funções para ajustar modelos ARIMA e modelos de suavização exponencial, enquanto que o pacote "prophet" do Python fornece uma implementação do modelo Prophet do Facebook para previsões de séries temporais. Isso permite que os usuários apliquem técnicas de previsão sofisticadas com relativa facilidade e eficiência.
Exemplos e aplicações
Em economia e finanças existem diversas aplicações interessantes para previsão de séries temporais. Destacamos alguns exemplos abaixo que servem de inspiração e que já foram abordados previamente neste espaço:
Os exemplos acima são relativamente mais avançados e exigem um conhecimento prévio sobre o tema, principalmente para quem nunca teve algum contato, mas servem de amostra do mar de possibilidades e aplicações de previsão de séries temporais.
Saiba mais
Este foi um artigo introdutório e uma visão geral sobre previsão de séries temporais, focando em entender conceitos básicos. Nos próximos artigos daremos continuidade ao tema explorando em mais detalhes os principais tópicos.
Para se aprofundar no assunto confira os cursos aplicados de R e Python da Análise Macro:
- Trilha de Macroeconomia Aplicada: https://conteudosam.com.br/pacotes/macroeconomia-aplicada/
- Trilha de Machine Learning e Econometria: https://conteudosam.com.br/pacotes/econometria-e-machine-learning/
- Modelos Preditivos: https://analisemacro.com.br/curso/modelos-preditivos-de-machine-learning/
- Econometria: https://analisemacro.com.br/cursos/econometria/introducao-a-econometria/
- Análise de Séries Temporais: https://conteudosam.com.br/cursos/analise-de-series-temporais/
Referências
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-03-05.