Gerar previsões quantitativas passa por satisfazer os seguintes passos: o quanto nós sabemos sobre os fatores que influenciam determinado evento ou variável? Existem dados disponíveis? O quanto as previsões que estamos fazendo podem afetar os eventos ou observações futuras? Satisfeita essas condições, podemos utilizar uma Regressão Linear para prever os valores de uma variável.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Introdução
Gerar previsões quantitativas passa por satisfazer os seguintes passos:
- O quanto nós sabemos sobre os fatores que influenciam determinado evento ou variável;
- Existem dados disponíveis?
- O quanto as previsões que estamos fazendo podem afetar os eventos ou observações futuras?
À medida que essas três condições são satisfeitas, é possível construir uma análise quantitativa, baseada na estimação de modelos estatísticos. Para tal, vamos considerar nessa seção regressões lineares, na qual construímos relações lineares entre nossa variável de interesse - aquela que estamos interessados em gerar previsões - e um conjunto de regressores.
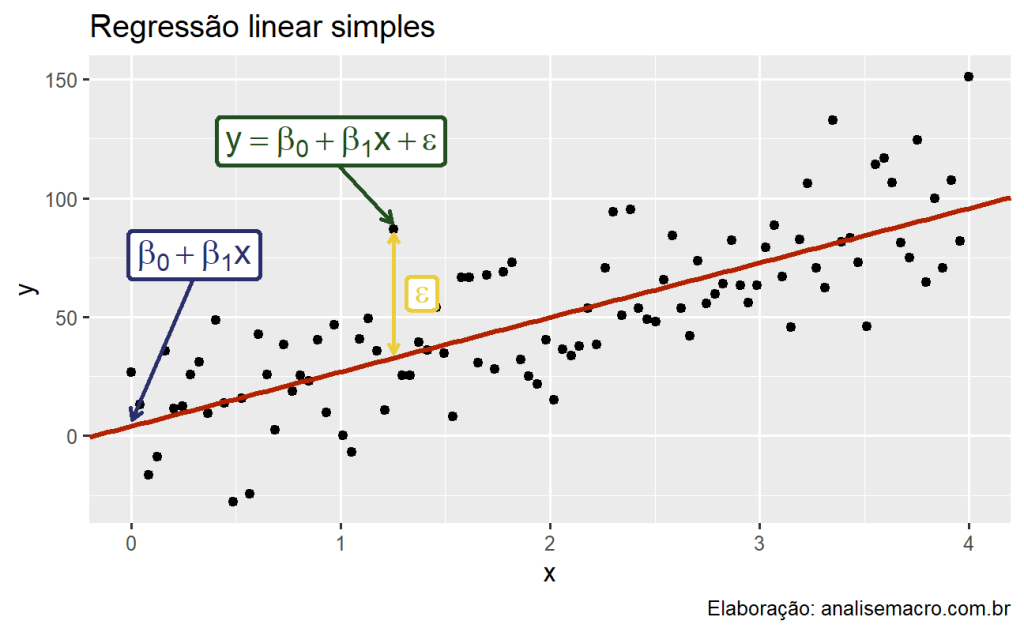
O modelo linear simples
Vamos manter as coisas de modo simples, por enquanto, e vamos assumir que e
se relacionam conforme se relacionam conforme
Isto é, e
se relacionam de maneira linear, onde
e
determinam o intercepto e a inclinação dessa relação, respectivamente. Note o indexador
, indicando que cada observação de
e
estão dispostas ao longo do tempo, e que portanto, possuem uma ordem definida, formando o que conhecemos como Regressão de Séries Temporais.
O intercepto determina o valor esperado de
quando
, enquanto
representa o incremento esperado em
resultante de uma mudança em uma unidade em
.
A relação acima é claramente não determinística, uma vez que admite-se um erro, representado por . Em outras palavras, tudo o que não for explicado por
, estará representado em
.
Podemos pensar, nesse contexto, em como a parte explicada do modelo e
como um erro aleatório. O erro, no caso, significa justamente o desvio em relação à linha subjacente da relação contida na equação da regressão.
Nós imaginamos que exista uma reta verdadeira representada por , mas nós não conhecemos
e
, logo nós devemos primeiro estimar esses parâmetros para depois obter a reta de regressão. Essa reta é, por fim, utilizada para fins de previsão. Para cada valor de
, nós podemos prever um valor correspondente de
fazendo uso de
.
Mínimos quadrados ordinários
Na prática, nós temos uma coleção de observações, mas não sabemos os valores de e
. Para conhecê-los, precisaremos estimá-los a partir dos dados disponíveis.
Existem, por suposto, muitas possibilidades para e
, com cada escolha gerando uma linha diferente.
O princípio de mínimos quadrados, que utilizaremos nessa seção, provê um maneira de escolher e
de forma efetiva minimizando a soma dos erros ao quadrado.
Isto é, nós escolhemos valores de e
que minimizam
o que leva a termos
onde e
são as médias de
e
. A linha estimada é conhecida como reta de regressão.
Regressão Múltipla
Vamos considerar agora um caso mais geral, isto é, aquele que envolve um conjunto finito de regressores. Aqui, portanto, teremos uma variável de interesse que queremos prever e diversos preditores. Em termos um pouco mais formais, nós especificamos um modelo estatístico do tipo:
onde e
são variáveis observáveis e
é não observável e refere-se a um termo de erro.
Os elementos em são parâmetros populacionais não conhecidos. A igualdade na equação anterior é supostamente válida para qualquer possível observação, ainda que tenhamos acesso a uma amostra com
observações. Nós, aliás, consideráremos essa amostra como uma realização de todas as potenciais amostras de tamanho
que poderíamos tomar da mesma população. Nesse caso, nós podemos considerar
e
como variáveis aleatórias.\footnote{Em outras palavras, cada observação corresponderá a uma realização dessas variáveis aleatórias.}
Nós podemos, a propósito, representar a equação em notação matricial, como abaixo:
onde é uma matriz
e
é uma matriz
.\footnote{Naturalmente,
será
.}
Ademais, também aqui podemos utilizar o método de mínimos quadrados ordinários de modo a obter .
Um ponto importante que devemos abordar aqui é a interpretação de um parâmetro qualquer. Para o caso simples, isso é mais direto. Aqui, entretanto, precisamos considerar aquelas suposições feitas sobre o termo de erro. Em particular, vamos novamente supor que
e
não são correlacionados. Isto é,
Por exemplo, qual o salário esperado para uma mulher aleatória de 40 anos com educação superior e 14 anos de experiência? Ou, qual a taxa de desemprego esperada dadas as taxas de salário, inflação e o produto total de uma economia? A primeira consequência da equação anterior é a interpretação individual dos coeficientes .
Por exemplo, mede a mudança esperada em
se
mudar em uma unidade mas todas as demais variáveis contidas em
permanecerem constantes.\footnote{Essa última chamada de condição ceteris paribus.}
Isto é,
{#eq-partial}
Assim, se estamos interessados em ver a relação entre e
, as demais variáveis em
são chamadas de variáveis de controle. Por exemplo, se estamos interessados em verificação a relação entre preço de imóveis e números de quartos, o tamanho do apartamento e a localização servem como controles para que consigamos verificar de forma mais precisa o que estamos interessados.
A depender do nosso interesse, podemos controlar para alguns fatores e não para outros. Se, por exemplo, incluir
, o efeito da
sobre
será dada por
O que significa o impacto da idade em , mantidas as demais variáveis constantes. A interpretação da equação como esperança condicional, a propósito, não necessariamente implica que podemos interpretar os parâmetros em
como uma medida de efeito causal de
sobre
. Por exemplo, não é improvável que a taxa de salários esperada varie entre trabalhadores casados ou não casados, mesmo após controlarmos por outros fatores, mas não é muito provável que casar cause maiores salários.
Premissas
Quando usamos o modelo de regressão linear, implicitamente assumimos algumas premissas sobre a equação anterior. Aqui vamos destacar algumas delas:
Primeiro, assumimos que o modelo é uma aproximação razoável da realidade, ou seja, a relação entre a variável dependente e as variáveis independentes satisfazem essa equação linear.
Segundo, assumimos as seguintes premissas sobre o termo de erro da regressão:
- Erros têm média zero, caso contrário, os valores previstos de serão sistematicamente tendenciosos;
- Erros não são autocorrelacionados, caso contrário, as previsões serão ineficientes, pois haveria mais informações nos dados que poderiam ser exploradas;
- Erros não têm relação com as variáveis independentes, caso contrário, haveria mais informações que deveriam ser incluídas na parte sistemática do modelo.
Também é útil ter os erros distribuídos normalmente com uma variância constante para produzir intervalos de previsão. Vale pontuar que as premissas podem variar conforme o método de estimação dos coeficientes.
Valores ajustados
As previsões de podem ser obtidas usando os coeficientes estimados na equação de regressão e definindo o termo de erro como zero. Em geral, escrevemos:
Substituindo os valores de ₜ para
, obtemos as previsões de
dentro do conjunto de treinamento, que são referidas como valores ajustados. É importante observar que essas são previsões dos dados utilizados para estimar o modelo, e não previsões genuínas de valores futuros de
.
Goodness-of-fit
Uma forma comum de resumir o quão bem um modelo de regressão linear se ajusta aos dados é através do coeficiente de determinação, ou R². Isso pode ser calculado como o quadrado da correlação entre os valores observados y e os valores previstos ŷ. Alternativamente, também pode ser calculado como:
,
onde as somatórias são realizadas em todas as observações. Dessa forma, ele reflete a proporção da variação na variável de previsão que é explicada pelo modelo de regressão.
Na regressão linear simples, o valor de também é igual ao quadrado da correlação entre
e
(supondo que uma intercepção foi incluída).
Se as previsões estão próximas dos valores reais, esperamos que esteja próximo de 1. Por outro lado, se as previsões não estão relacionadas aos valores reais, então
= 0 (novamente, assumindo que há uma intercepção). Em todos os casos,
está compreendido entre 0 e 1.
O valor de é frequentemente utilizado, embora muitas vezes de forma incorreta, em previsões. O valor de
nunca diminuirá ao adicionar um preditor extra ao modelo, e isso pode levar ao superajuste. Não existem regras definidas para o que é um bom valor de
, e os valores típicos de
dependem do tipo de dados utilizados. Validar o desempenho de previsão de um modelo nos dados de teste é muito melhor do que medir o valor de
nos dados de treinamento.
Avaliando um modelo de regressão
As diferenças entre os valores observados de y e os valores ajustados correspondentes ^y são os erros do conjunto de treinamento ou "resíduos" definidos como,
Os resíduos têm algumas propriedades úteis, incluindo as seguintes duas:
Após selecionar as variáveis de regressão e ajustar o modelo de regressão, é necessário plotar os resíduos para verificar se as suposições do modelo foram satisfeitas. Existem uma série de gráficos que devem ser produzidos para verificar diferentes aspectos do modelo ajustado e das suposições subjacentes. Vamos discutir cada um deles a seguir.
Gráfico ACF dos resíduos
Com dados de séries temporais, é altamente provável que o valor de uma variável observado no período atual seja semelhante ao seu valor no período anterior, ou até mesmo no período anterior a esse, e assim por diante. Portanto, ao ajustar um modelo de regressão a dados de séries temporais, é comum encontrar autocorrelação nos resíduos.
Nesse caso, o modelo estimado viola a suposição de não autocorrelação nos erros, e nossas previsões podem ser ineficientes - há alguma informação remanescente que deve ser considerada no modelo para obter previsões melhores. As previsões de um modelo com erros autocorrelacionados ainda são imparciais, portanto elas não estão "erradas", mas geralmente terão intervalos de previsão maiores do que o necessário. Portanto, sempre devemos analisar um gráfico ACF dos resíduos.
Histograma dos resíduos
Sempre é uma boa ideia verificar se os resíduos seguem uma distribuição normal. Como explicamos anteriormente, isso não é essencial para a previsão, mas facilita o cálculo dos intervalos de previsão.
Gráficos de resíduos em relação aos preditores
Esperamos que os resíduos estejam dispersos aleatoriamente sem mostrar quaisquer padrões sistemáticos. Uma forma simples e rápida de verificar isso é examinar gráficos de dispersão dos resíduos em relação a cada uma das variáveis preditoras. Se esses gráficos de dispersão mostrarem um padrão, então a relação pode ser não linear e o modelo precisará ser modificado de acordo.
Também é necessário plotar os resíduos em relação a quaisquer preditores que não estejam no modelo. Se algum desses mostrar um padrão, então o preditor correspondente pode precisar ser adicionado ao modelo (possivelmente em uma forma não linear).
Gráficos de resíduos em relação aos valores ajustados
Um gráfico dos resíduos em relação aos valores ajustados também não deve mostrar padrão. Se for observado um padrão, pode haver "heteroscedasticidade" nos erros, o que significa que a variância dos resíduos pode não ser constante. Se esse problema ocorrer, pode ser necessária uma transformação da variável de previsão, como um logaritmo ou raiz quadrada.
Outliers e observações influentes
Observações que assumem valores extremos em comparação com a maioria dos dados são chamadas de outliers. Observações que têm uma grande influência nos coeficientes estimados de um modelo de regressão são chamadas de observações influentes. Geralmente, observações influentes também são outliers que são extremos na direção
Existem métodos formais para detectar outliers e observações influentes que estão além do escopo deste livro didático. Um gráfico de dispersão de em relação a cada
é sempre um ponto de partida útil na análise de regressão e frequentemente ajuda a identificar observações incomuns.
Uma fonte de outliers é a entrada incorreta de dados. Estatísticas descritivas simples dos seus dados podem identificar mínimos e máximos que não fazem sentido. Se tal observação for identificada e tiver sido registrada incorretamente, ela deve ser corrigida ou removida imediatamente da amostra.
Outliers também ocorrem quando algumas observações são simplesmente diferentes. Nesse caso, pode não ser sábio remover essas observações. Se uma observação foi identificada como provável outlier, é importante estudá-la e analisar as possíveis razões por trás dela. A decisão de remover ou manter uma observação pode ser desafiadora (especialmente quando os outliers são observações influentes). É recomendável relatar os resultados tanto com quanto sem a remoção de tais observações.
Regressão Espúria
Na maioria das vezes, dados de séries temporais são "não estacionários"; isto é, os valores da série temporal não flutuam em torno de uma média constante ou com uma variância constante. Aqui precisamos abordar o efeito que dados não estacionários podem ter em modelos de regressão.
Regressões de séries temporais não estacionárias podem levar a regressões espúrias. Alto e alta autocorrelação residual podem ser sinais de regressão espúria.
Casos de regressão espúria podem parecer fornecer previsões razoáveis a curto prazo, mas geralmente não continuarão funcionando no futuro.
Preditores úteis
É possível adicionar alguns preditores úteis, que descrevem características especifícias de séries temporais para melhorar a previsão:
Tendência
É comum para séries temporais possuírem tendência. Uma tendência linear pode ser modelada utilizando como preditor.
Dummys
Uma variável desse tipo pode surgir, por exemplo, ao prever vendas diárias e você deseja levar em conta se o dia é um feriado público ou não. Portanto, o preditor assume o valor "sim" em um feriado público e "não" em outros dias.
Essa situação ainda pode ser tratada dentro do contexto de modelos de regressão múltipla, criando uma "variável dummy" que assume o valor 1 correspondente a "sim" e 0 correspondente a "não". Uma variável dummy também é conhecida como "variável indicadora".
Uma variável dummy também pode ser usada para considerar um valor atípico nos dados. Em vez de omitir o valor atípico, uma variável dummy remove seu efeito. Nesse caso, a variável dummy assume o valor 1 para essa observação e 0 em todos os outros casos.
Defasagens Distribuídas
Por vezes, algumas variáveis possuem efeitos defasados sobre outras, e portanto, é necessário adicionar sua(s) defasagens como preditores.
Variáveis de intervenção
É frequentemente necessário modelar intervenções que podem ter afetado a variável a ser prevista. Por exemplo, atividade da concorrência, gastos com publicidade, greves industriais, entre outros, podem ter um efeito.
Quando o efeito dura apenas por um período, usamos uma "variável spike" (pico). Essa é uma variável dummy que assume o valor um no período da intervenção e zero nos outros períodos. Uma variável spike é equivalente a uma variável dummy para lidar com um valor atípico.
Outras intervenções têm um efeito imediato e permanente. Se uma intervenção causa uma mudança de nível (ou seja, o valor da série muda de forma repentina e permanente a partir do momento da intervenção), então usamos uma "variável step" (degrau). Uma variável step assume valor zero antes da intervenção e valor um a partir do momento da intervenção.
Outra forma de efeito permanente é uma mudança de inclinação. Nesse caso, a intervenção é tratada usando uma tendência linear em partes; uma tendência que muda de direção no momento da intervenção e, portanto, é não linear.
Previsão com Regressão Linear
Lembre-se de que as previsões de podem ser obtidas usando
que compreende os coeficientes estimados e ignora o erro na equação de regressão. Substituir os valores das variáveis preditoras retorna os valores ajustados (conjunto de treinamento) de
. No entanto, o que estamos interessados aqui é prever valores futuros de
.
Previsões ex-ante versus ex-post
Ao usar modelos de regressão para dados de séries temporais, é necessário distinguir entre os diferentes tipos de previsões que podem ser produzidas, dependendo do que se assume como conhecido quando as previsões são calculadas.
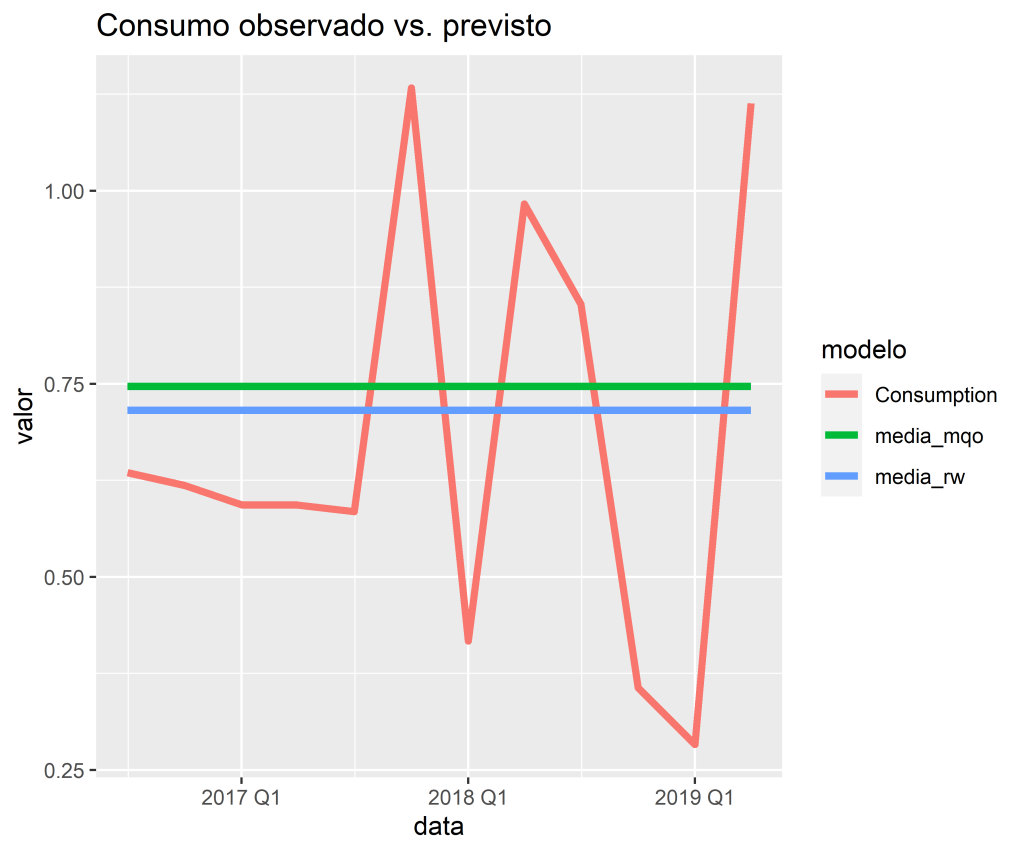
Previsões ex-ante são aquelas feitas usando apenas as informações disponíveis antecipadamente. Por exemplo, previsões ex-ante para a mudança percentual no consumo nos Estados Unidos para trimestres após o final da amostra, devem usar apenas informações disponíveis até e incluindo o 2º trimestre de 2019. Essas são previsões genuínas, feitas antecipadamente usando todas as informações disponíveis na época. Portanto, para gerar previsões ex-ante, o modelo requer previsões dos preditores.
Previsões ex-post são aquelas feitas usando informações posteriores sobre os preditores. Por exemplo, previsões ex-post de consumo podem usar as observações reais dos preditores, assim que essas observações forem feitas. Essas não são previsões genuínas, mas são úteis para estudar o comportamento dos modelos de previsão.
O modelo a partir do qual as previsões ex-post são produzidas não deve ser estimado usando dados do período de previsão. Ou seja, as previsões ex-post podem assumir conhecimento das variáveis preditoras (as variáveis ), mas não devem assumir conhecimento dos dados que serão previstos (a variável
).
Uma avaliação comparativa das previsões ex-ante e ex-post pode ajudar a separar as fontes de incerteza das previsões. Isso mostrará se os erros de previsão surgiram devido a previsões pobres dos preditores ou devido a um modelo de previsão inadequado.
Exemplo de Análise de Regressão e Previsão
Para ilustrar, vamos usar os dados disponíveis no dataset us_change.
Vamos estimar a equação dada por
1. Estimação
| .model | term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|
| lm | (Intercept) | 0.2531051 | 0.0344704 | 7.342673 | 0.0000000 |
| lm | Income | 0.7405835 | 0.0401150 | 18.461493 | 0.0000000 |
| lm | Savings | -0.0528901 | 0.0029241 | -18.087537 | 0.0000000 |
| lm | Unemployment | -0.1746853 | 0.0955107 | -1.828959 | 0.0689490 |
| lm | Production | 0.0471726 | 0.0231420 | 2.038397 | 0.0428744 |
2. Previsões
3. Acurácia
| .model | .type | ME | RMSE | MAE | MPE | MAPE | MASE | RMSSE | ACF1 |
|---|---|---|---|---|---|---|---|---|---|
| lm | Test | -0.0661579 | 0.2782591 | 0.2489894 | -30.51928 | 47.79536 | NaN | NaN | -0.3026298 |
| rw | Test | -0.0352577 | 0.2725699 | 0.2386893 | -25.11657 | 44.43713 | NaN | NaN | -0.3026298 |
4. Previsão fora da amostra
___________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.
Referências
Hyndman, R. J., e G. Athanasopoulos. 2013. Forecasting: Principles and Practice. OTexts.

![Rendered by QuickLaTeX.com \[\sum_{t=1}^T \varepsilon_t^2 = \sum_{t=1}^T (y_t - \beta_{0} - \beta_{1} x_{i,t} )^2.\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-e2f14ee3cccf6a3669e13d771f5e49d2_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\beta_{1}} = \frac{\sum_{i=1}^{N} (y_{i} - \bar{y})(x_{i} - \bar{x})}{\sum_{i=1}^{N} (x_{i} - \bar{x})^{2}}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-b9466d749a5ac121adbca75bcd47a18e_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{t=1}^{T}{e_t}=0 \quad\text{e}\quad \sum_{t=1}^{T}{x_{k,t}e_t}=0\qquad\text{para todo k}.\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-269c4af8a18cc13a00cd94cfa1dc072e_l3.png)