Estimando uma Curva IS para o Brasil

[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

A primeira parte do nosso Curso de Macroeconometria usando o R é dedicada a entender o organismo econômico por meio da estimação de quatro equações: uma Curva de Phillips, que representa o lado da oferta; uma Curva IS, que representa o lado da demanda; uma Paridade da Taxa de Juros, que representa o contato com o resto do mundo; e uma Curva de Reação do Banco Central. Nesse post, por suposto, ilustramos alguns resultados da estimação da Curva IS, utilizando dados brasileiros. Todos os códigos e orientações sobre como proceder a estimação no R são mostrados no nosso curso.

Metodologia e Dados

Com base em Blinder (1999), Bogdanski et al. (2000) e Walsh (2010), nós estimaremos a seguinte Curva IS:

(1)  

onde é o hiato do produto, é o juro nominal, é a expectativa de inflação 12 meses à frente, é a taxa de juros neutra e são as necessidades de financiamento do setor público. As séries que utilizaremos para estimar 1 são o PIB mensal do IBRE/FGV, o juro real ex-post (taxa Selic deflacionada pela inflação acumulada em 12 meses medida pelo IPCA), o juro real ex-ante (taxa Selic deflacionada pela expectativa de inflação medida pelo IPCA e acumulada em 12 meses) e a série de superávit primário acumulado em 12 meses controlado pelo PIB, com sinal trocado. Os dados brutos são importados abaixo.

### Importar dados
data = read.table('data.csv', header=T, sep=';', dec=',')
data$date = as.Date(dataexpost, type='lambda', freq=14400)
neutro = hp$trend

Abaixo, um gráfico do diferencial de juros.

O próximo passo é criar o hiato do produto. O código abaixo faz isso.

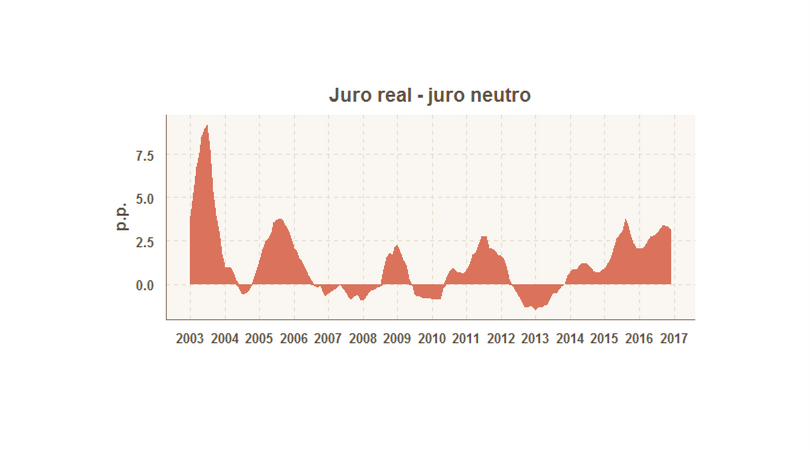
hp2 = hpfilter(data$pib, type='lambda', freq=14400)
hiato = hp2$cycle

Criado o diferencial de juros e o hiato do produto, podemos colocar os dados que utilizaremos em uma mesma estrutura.

hiato = ts(hiato, start=c(2003,01), freq=12)
diferencial = ts(diferencial, start=c(2003,01), freq=12)
data = ts(data[,-1], start=c(2003,01), freq=12)
is = ts.intersect(hiato, diferencial, data[,4])
colnames(is) = c('Hiato', 'DJuros', 'NFSP')

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/11/datascience.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][et_pb_text admin_label="Texto" background_layout="light" text_orientation="center" use_border_color="off" border_color="#ffffff" border_style="solid"]

Clique na figura para conhecer os cursos aplicados em R da Análise Macro!

[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/04/painel.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/cursos-de-econometria/dados-em-painel/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][et_pb_text admin_label="Texto" background_layout="light" text_orientation="center" use_border_color="off" border_color="#ffffff" border_style="solid"]

Clique na figura para conhecer nosso novo curso de econometria

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

Organizados os dados, podemos estimar 1 com a função dynlm do pacote de mesmo nome. O código abaixo faz isso.

modelo = dynlm(Hiato~lag(Hiato, -1)+lag(Hiato,-2)+lag(DJuros,-1)+
 lag(NFSP,-1), data=is)

A tabela 1 traz os resultados da estimação. Observe que o coeficiente do diferencial de juros é de -0,11. Isso significa que um aumento de um ponto percentual no diferencial de juros, reduz o hiato do produto em -0,11. Ademais, observa-se que o mesmo é estatisticamente significativo. O coeficiente das necessidades de financiamento do setor público, por seu turno, não se mostrou estatisticamente significativo.

Essa seção do nosso Curso de Macroeconometria usando o R completou aquelas quatro equações vistas no modelo básico do Banco Central. Estimamos uma Curva de Phillips, uma Curva IS, uma Curva de Reação do Banco Central e uma equação de paridade da taxa de juros. Esperamos, com efeito, que todo esse trabalho de modelagem amplie os insights por trás da teoria macroeconômica.

[/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/09/est.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/introducao-a-estatistica/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][/et_pb_column][et_pb_column type="1_2"][et_pb_code admin_label="Código"]<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td><em>Dependent variable:</em></td></tr> <tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr> <tr><td style="text-align:left"></td><td>Hiato</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">lag(Hiato, -1)</td><td>0.969^***</td></tr> <tr><td style="text-align:left"></td><td>(0.077)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">lag(Hiato, -2)</td><td>-0.144^*</td></tr> <tr><td style="text-align:left"></td><td>(0.077)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">lag(DJuros, -1)</td><td>-0.110^***</td></tr> <tr><td style="text-align:left"></td><td>(0.041)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">lag(NFSP, -1)</td><td>0.024</td></tr> <tr><td style="text-align:left"></td><td>(0.046)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">Constant</td><td>0.177</td></tr> <tr><td style="text-align:left"></td><td>(0.139)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>166</td></tr> <tr><td style="text-align:left">R²</td><td>0.770</td></tr> <tr><td style="text-align:left">Adjusted R²</td><td>0.764</td></tr> <tr><td style="text-align:left">Residual Std. Error</td><td>1.024 (df = 161)</td></tr> <tr><td style="text-align:left">F Statistic</td><td>134.416^*** (df = 4; 161)</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td style="text-align:right">^*p<0.1; ^**p<0.05; ^***p<0.01</td></tr> </table>[/et_pb_code][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_team_member admin_label="Pessoa" saved_tabs="all" name="Vítor Wilher " position="Data Scientist" image_url="https://analisemacro.com.br/wp-content/uploads/2011/03/vitorwilhergnews.png" animation="left" background_layout="light" facebook_url="https://www.facebook.com/vitor.wilher.9" twitter_url="https://twitter.com/vitorwilherbr" linkedin_url="https://www.linkedin.com/in/v%C3%ADtor-wilher-78164024" use_border_color="off" border_color="#ffffff" border_style="solid"]

Vítor Wilher é Bacharel e Mestre em Economia, pela Universidade Federal Fluminense, tendo se especializado na construção de modelos macroeconométricos, política monetária e análise da conjuntura macroeconômica doméstica e internacional. Tem, ademais, especialização em Data Science pela Johns Hopkins University. Sua dissertação de mestrado foi na área de política monetária, titulada "Clareza da Comunicação do Banco Central e Expectativas de Inflação: evidências para o Brasil", defendida perante banca composta pelos professores Gustavo H. B. Franco (PUC-RJ), Gabriel Montes Caldas (UFF), Carlos Enrique Guanziroli (UFF) e Luciano Vereda Oliveira (UFF). Já trabalhou em grandes empresas, nas áreas de telecomunicações, energia elétrica, consultoria financeira e consultoria macroeconômica. É o criador da Análise Macro, startup especializada em treinamento e consultoria em linguagens de programação voltadas para data analysis, sócio da MacroLab Consultoria, empresa especializada em cenários e previsões e fundador do hoje extinto Grupo de Estudos sobre Conjuntura Econômica (GECE-UFF). É também Visiting Professor da Universidade Veiga de Almeida, onde dá aulas nos cursos de MBA da instituição, Conselheiro do Instituto Millenium e um dos grandes entusiastas do uso do R no ensino. Leia os posts de Vítor Wilher aqui. Caso queira, mande um e-mail para ele: vitorwilher@analisemacro.com.br

[/et_pb_team_member][/et_pb_column][/et_pb_row][/et_pb_section]