Nível de atividade, inflação e a Curva de Phillips

[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

O objetivo principal da Análise Macro é melhorar o ensino de economia no país, provendo alunos, professores e profissionais de mercado de ferramentas estatísticas e econométricas que facilitam o trabalho com a melhor evidência empírica disponível, fazendo com que teorias econômicas sem sentido sejam rejeitadas. Um objetivo secundário é contribuir com o debate econômico, melhorando a compreensão desses agentes sobre fatos e conceitos econômicos, através de exercícios empíricos. O primeiro é cumprido através do Clube do Código e de cursos aplicados de R ofertados mensalmente, já o segundo é alcançado por meio desse Blog. Isso dito, vamos aqui esclarecer um ponto já levantado diversas vezes no Clube do Código e no nosso Curso de Macroeconometria usando o R: a relação entre nível de atividade e inflação.

Há uma literatura empírica bastante consolidada que mostra o quanto a relação entre o nível de atividade e a inflação se mostra fraca, com primazia das expectativas e da inércia para explicar a inflação efetiva. Seguindo o arcabouço da Curva de Phillips, para o Brasil, pode-se ver uma resenha da literatura, bem como alguns resultados que evidenciam essa fraqueza em Sachsida et al. (2012). Para os Estados Unidos, um paper bastante citado sobre o assunto é Galí e Gertler (2000). Esses resultados, ademais, estão em linha com a teoria econômica, sintetizada, por exemplo, em Woodford (2003). Em outras palavras, para quem é do ramo, não há a menor novidade em se dizer que se o Banco Central quiser controlar a inflação, ele precisará ancorar as expectativas de inflação dos agentes econômicos e que não há uma relação robusta entre nível de atividade e inflação.

Isso dito, me surpreende toda vez que vejo algum comentário por aqui que ignora essas evidências. Para tentar elucidar a questão de um ponto de vista prático, podemos verificar a relação entre o nível de atividade e a inflação. O código abaixo baixa os dados da inflação mensal, do PIB mensal do IBRE/FGV e das expectativas de inflação mensal do boletim Focus.

library(XLConnect)
library(ggplot2)
library(png)
library(grid)
library(BETS)
library(mFilter)
library(dynlm)
library(astsa)
library(stargazer)

### Baixar dados do PIB, da Inflação e das expectativas
url = 'http://bit.ly/2l3KKFY'
temp = tempfile()
download.file(url, destfile=temp, mode='wb')
data = loadWorkbook(temp)
pib_sa = ts(readWorksheet(data, sheet = 6, header = TRUE, 
 startRow = 3)[,17], start=c(2000,01), freq=12)

inflacao = window(BETS.get(433), start=c(2000,01))

expectativa = ts(read.csv2('expectativa.csv', 
 header=T, 
 sep=';', dec=',')[,2], 
 start=c(2001,11), freq=12)

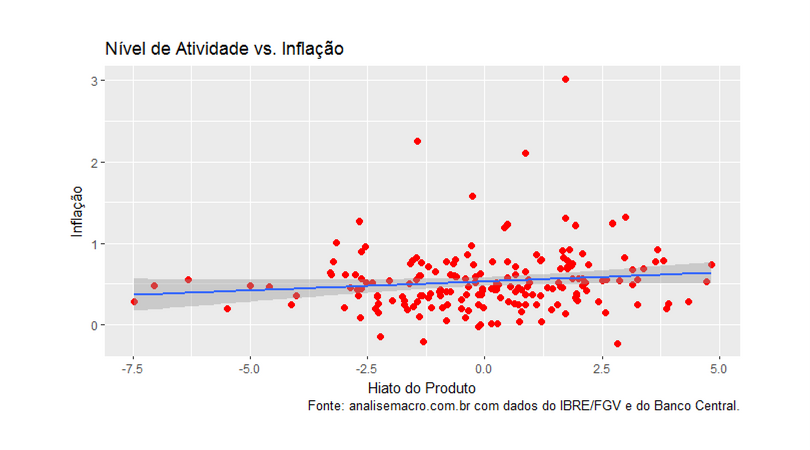
No gráfico abaixo, plotamos o nível de atividade representado pelo hiato do produto contra a inflação mensal.

Como se vê, a relação entre o hiato do produto e a inflação é baixa. Alguém, a propósito, poderia alegar que existiria alguma defasagem nessa relação. Para verificar isso, podemos plotar a inflação contra as defasagens do hiato do produto. Isso é feito abaixo.

De forma a confirmar a fraqueza dessa relação, bem como de ratificar a importância das expectativas e da inércia para explicar a inflação efetiva, podemos estimar uma Curva de Phillips como

(1)  

onde é a inflação mensal efetiva, é a expectativa em para a inflação em , é o hiato do produto e é um ruído branco.

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

A tabela ao lado mostra as estimativas de (1) via Mínimos Quadrados em Dois Estágios (TSLS). Observe que o componente regressivo e as expectativas de inflação se mostram estatisticamente significativas para explicar a inflação efetiva. Já o hiato do produto não apresenta significância. Esse resultado, disponível para qualquer um que se dê o trabalho de acessar os dados e estimar (1), está consolidado na literatura empírica sobre o assunto, como dito acima.

Sob esse aspecto, não deixa de ser surpreendente que alguns ainda argumentem que a recessão atual é a grande causadora da queda da inflação que assistimos. Ou vejam alguma relação robusta entre nível de atividade e inflação, quando a literatura empírica e a teoria econômica associam o controle da inflação à ancoragem das expectativas.

Será que esses conhecem a literatura sobre o assunto ou mesmo a teoria econômica? É o caso de se perguntar, não é mesmo, leitor amigo? 🙂

[/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/06/liberte-se.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][et_pb_text admin_label="Texto" background_layout="light" text_orientation="center" use_border_color="off" border_color="#ffffff" border_style="solid"]

Clique na figura para conhecer os nossos Cursos

[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_code admin_label="Código"]<table style="text-align:center"><tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td>Inflação mensal</td></tr> <tr><td></td><td colspan="1" style="border-bottom: 1px solid black"></td></tr> <tr><td style="text-align:left"></td><td>inflacao</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Inflação(-1)</td><td>0.555^***</td></tr> <tr><td style="text-align:left"></td><td>(0.055)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">Expectativa</td><td>0.675^***</td></tr> <tr><td style="text-align:left"></td><td>(0.120)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">Hiato(-1)</td><td>0.013</td></tr> <tr><td style="text-align:left"></td><td>(0.008)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td style="text-align:left">Intercepto</td><td>-0.074</td></tr> <tr><td style="text-align:left"></td><td>(0.051)</td></tr> <tr><td style="text-align:left"></td><td></td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td>189</td></tr> <tr><td style="text-align:left">R²</td><td>0.593</td></tr> <tr><td style="text-align:left">Adjusted R²</td><td>0.586</td></tr> <tr><td style="text-align:left">Residual Std. Error</td><td>0.248 (df = 185)</td></tr> <tr><td style="text-align:left">F Statistic</td><td>89.743^*** (df = 3; 185)</td></tr> <tr><td colspan="2" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td style="text-align:right">^*p<0.1; ^**p<0.05; ^***p<0.01</td></tr> </table>[/et_pb_code][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]

_________________________________________________________________________________________

Referências:

Galí, J.; Gertler, M. (2000). Inflation Dynamics: a structural econometric analysis. NBER Working Paper nº 7551

Sachsida, A.; Mendonça, M. J. C.; Medrano, L. A. T (2012). Inflação versus Desemprego: novas evidências para o Brasil. Economia Aplicada, 16(3): 475-500

Woodford, M. (2003). Interest and Prices. New Jersey: Princeton Press

[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="4_4"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/06/woold.png" show_in_lightbox="off" url="https://analisemacro.com.br/clube-do-codigo/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="1_3"][et_pb_gallery admin_label="Galeria" gallery_ids="17132,17133,17134" fullwidth="on" show_title_and_caption="off" show_pagination="off" background_layout="light" auto="on" auto_speed="6000" hover_overlay_color="rgba(255,255,255,0.9)" caption_all_caps="off" use_border_color="off" border_color="#ffffff" border_style="solid" saved_tabs="all"] [/et_pb_gallery][et_pb_gallery admin_label="Galeria" gallery_ids="17136,17137,17138" fullwidth="on" show_title_and_caption="off" show_pagination="off" background_layout="light" auto="on" auto_speed="6000" hover_overlay_color="rgba(255,255,255,0.9)" caption_all_caps="off" use_border_color="off" border_color="#ffffff" border_style="solid" saved_tabs="all"] [/et_pb_gallery][/et_pb_column][et_pb_column type="2_3"][et_pb_team_member admin_label="Pessoa" saved_tabs="all" name="Vítor Wilher " position="Data Scientist" animation="left" background_layout="light" facebook_url="https://www.facebook.com/vitor.wilher.9" twitter_url="https://twitter.com/vitorwilherbr" linkedin_url="https://www.linkedin.com/in/v%C3%ADtor-wilher-78164024" use_border_color="off" border_color="#ffffff" border_style="solid"]

Vítor Wilher é Bacharel e Mestre em Economia, pela Universidade Federal Fluminense, tendo se especializado na construção de modelos macroeconométricos, política monetária e análise da conjuntura macroeconômica doméstica e internacional. Tem, ademais, especialização em Data Science pela Johns Hopkins University. Sua dissertação de mestrado foi na área de política monetária, titulada "Clareza da Comunicação do Banco Central e Expectativas de Inflação: evidências para o Brasil", defendida perante banca composta pelos professores Gustavo H. B. Franco (PUC-RJ), Gabriel Montes Caldas (UFF), Carlos Enrique Guanziroli (UFF) e Luciano Vereda Oliveira (UFF). Já trabalhou em grandes empresas, nas áreas de telecomunicações, energia elétrica, consultoria financeira e consultoria macroeconômica. É o criador da Análise Macro, startup especializada em treinamento e consultoria em linguagens de programação voltadas para data analysis, sócio da MacroLab Consultoria, empresa especializada em cenários e previsões e fundador do hoje extinto Grupo de Estudos sobre Conjuntura Econômica (GECE-UFF). É também Visiting Professor da Universidade Veiga de Almeida, onde dá aulas nos cursos de MBA da instituição, Conselheiro do Instituto Millenium e um dos grandes entusiastas do uso do R no ensino. Leia os posts de Vítor Wilher aqui. Caso queira, mande um e-mail para ele: vitorwilher@analisemacro.com.br

[/et_pb_team_member][/et_pb_column][/et_pb_row][/et_pb_section]