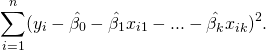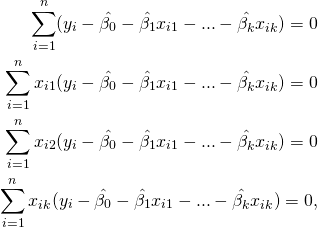Estimando regressões múltiplas com o R

[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Abel||||" text_font_size="21" use_border_color="off" border_color="#ffffff" border_style="solid"]

A turma de setembro do nosso Curso de Introdução à Econometria usando o R terá uma grande novidade. A apostila e as listas de exercício foram revisadas e atualizadas com exercícios do livro clássico de Jeffrey Marc Wooldridge. Todos feitos no R, de modo a mostrar para o aluno como a teoria pode ser complementada com a prática. Com isso, trazemos ainda mais aplicações para o curso, o que garante total absorção do conteúdo. Para ilustrar, vamos considerar nesse post o modelo de regressão múltipla. Primeiro, um pouco de teoria e depois um exemplo do Wooldridge feito no R.

[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2018/08/ultimasemanasetembro.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="off" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]

[/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Abel||||" text_font_size="21" use_border_color="off" border_color="#ffffff" border_style="solid"]

Em post anterior nesse blog, vimos o modelo de regressão simples, onde $y$ pode ser explicado por uma única variável $x$ . O problema básico desse tipo de análise é que ela faz uma suposição bastante forte, qual seja, que $x$ não está correlacionado com o erro, dificultando a aplicação da condição ceteris paribus. A análise de regressão múltipla, por outro lado, é mais receptiva a esse tipo de condição, uma vez que ela permite que controlemos outros fatores que afetam $y$ , adicionando os mesmos na equação. Assim, por suposto, se queremos explicar $y$ , podemos utilizar $k$ variáveis, como abaixo:

(1) $\begin{align*} y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + ... + \beta_k x_k + u, \end{align*}$

onde $\beta_0$ é o intercepto, $\beta_k$ é o parâmetro associado a $x_k$ . De modo a obter uma estimativa para 1, devemos observar que

(2) $\begin{align*} E(u|x_1, x_2, ..., x_k) = 0. \end{align*}$

Isto é, que todos os fatores no termo de erro não observado $u$ sejam não correlacionados com as variáveis explicativas. De modo a obter estimativas para os $\beta_k$ parâmetros, é possível recorrer ao método de mínimos quadrados ordinários. Isto é, dado

(3) $\begin{align*} \hat{y} = \hat{\beta_0} + \hat{\beta_1} x_1 + \hat{\beta_2} x_2 + ... + \hat{\beta_k} x_k, \end{align*}$

onde $\hat{\beta_k}$ é a estimativa de $\beta_k$ , o método de MQO escolhe as estimativas $\hat{\beta_k}$ que minimizam a soma dos quadrados dos resíduos:

(4) $\begin{align*} \sum_{i=1}^{n} (y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - ... - \hat{\beta_k} x_{ik})^2. \end{align*}$

O problema acima pode ser resolvido por meio de cálculo multivariado, de onde obtemos as condições de primeira ordem

(5) $\begin{align*} \sum_{i=1}^{n} (y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - ... - \hat{\beta_k} x_{ik}) = 0 \nonumber \\ \sum_{i=1}^{n} x_{i1} (y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - ... - \hat{\beta_k} x_{ik}) = 0 \nonumber \\ \sum_{i=1}^{n} x_{i2}(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - ... - \hat{\beta_k} x_{ik}) = 0 \nonumber \\ \sum_{i=1}^{n} x_{ik}(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - ... - \hat{\beta_k} x_{ik}) = 0, \nonumber \end{align*}$

ou simplesmente, $E(u) = 0$ e $E(x_j u) = 0$ .

Interpretação da equação de regressão de MQO

Suponha, agora, que tenhamos

(6) $\begin{align*} \hat{y} = \hat{\beta_0} + \hat{\beta_1} x_1 + \hat{\beta_2} x_2. \end{align*}$

O intercepto $\beta_0$ será então o valor previsto de $y$ quando $x_1 = x_2 = 0$ . Já as estimativas $\hat{\beta_1}$ e $\hat{\beta_2}$ devem ser interpretadas como efeito parcial ou simplesmente ceteris paribus. Isto é,

(7) $\begin{align*} \Delta \hat{y} = \hat{\beta_1} \Delta x_1 + \hat{\beta_2} \Delta x_2, \nonumber \end{align*}$

de modo que obtemos a variação prevista em $y$ dadas as variações em $x_1$ e $x_2$ . Em particular, quando $x_2$ é mantido fixo, de modo que $\Delta x_2 = 0$ , teremos

(8) $\begin{align*} \Delta \hat{y} = \hat{\beta_1} \Delta x_1. \nonumber \end{align*}$

Ou, simplesmente,

(9) $\begin{align*} \frac{\partial \hat{y}}{\partial \hat{x_1}} = \hat{\beta_1}, \nonumber \end{align*}$

onde $\hat{\beta_1}$ irá medir o efeito da variação de $x_1$ em $y$ , mantido $x_2$ constante.

Exemplo: equação do salário-hora

De modo a ilustrar, vamos considerar o exemplo 3.2 do livro do Wooldridge, em que o mesmo utiliza o conjunto de dados wage1, disponível no pacote wooldridge. Ele pode ser acessado como abaixo.


data(wage1, package='wooldridge')

De posse desse conjunto de dados, você pode estimar o modelo abaixo:


lm(log(wage) ~ educ+exper+tenure, data=wage1)

De modo a obter a seguinte reta de regressão para o log do salário-hora

(10) $\begin{align*} \hat{log(wage)} = 0.284 + 0.092 educ + 0.0041 exper + 0.022 tenure. \end{align*}$

De onde se conclui, por exemplo, que o aumento de um ano na educação formal equivale a um aumento de 9.2\% no salário-hora, mantidos exper e tenure fixos.

[/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2018/08/coversetembro.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="off" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]

[/et_pb_image][/et_pb_column][/et_pb_row][/et_pb_section]

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Inflação de Serviços vs. Desemprego

Modelo de previsão para grupos do IPCA

Text mining dos comunicados do FOMC: prevendo mudanças na política

Analisando a inflação por faixa de renda no Python

Criando o Fator de Momentum para o Brasil [Python]

O IBC-Br é um bom preditor do PIB?

Outros artigos relacionados

Inflação de Serviços vs. Desemprego

A teoria econômica convencional sugere a presença de um trade-off entre inflação e desemprego no curto prazo, comumente conhecido como a Curva de Phillips. Em

Modelo de previsão para grupos do IPCA

Neste artigo investigamos se a previsão desagregada da inflação é capaz de gerar previsões mais acuradas do que a previsão agregada. Utilizamos o Índice Nacional de Preços ao Consumidor Amplo (IPCA) como medida de interesse, aplicando um modelo simples e um modelo de passeio aleatório para comparação. Todo o processo pode ser feito de maneira automatizada utilizando a linguagem de programação R.

Text mining dos comunicados do FOMC: prevendo mudanças na política

Como quantificar sentimentos e emoções a partir de comunicados de política monetária? Neste exercício utilizamos os statements do FOMC para construir um índice de sentimentos, o que permite comparar a "narrativa" com a prática da política monetária, ou seja, mudanças da taxa de juros. Também avaliamos se tal índice é útil em prever mudanças de política através do teste de causalidade de Granger.