Ao calcular um parâmetro populacional, realiza-se uma estimação pontual, entretanto, ao realizar a estimação através de uma amostra, é possível obter uma amplitude de possíveis valores dentro dos quais os verdadeiros valores da estimação podem se encontrar. Como é possível construir um intervalo em que há confiança nos valores estimados? No post de hoje, mostramos uma solução para este problema, conceituando o Intervalo de Confiança e realizando um exemplo com o R.
Ao contrário da estimação pontual/estatística amostral, que calcula o valor de um parâmetro populacional não conhecido como apenas um único valor, o intervalo de confiança entrega o que podemos entender como uma amplitude de possíveis valores deste parâmetro.
Basicamente: queremos encontrar, por exemplo, a média . Podemos calcular um único valor, porém, é possível também calcular uma amplitude de possíveis valores, no qual podemos ter a confiança de que os pontos estimados estejam em determinado intervalo dado uma suposição.
E como definir o Intervalo de Confiança? O IC é definido em 90% =< IC =< 99%. Outra forma de definir o IC é através do nível de significância (![]() ), calculando como IC = 1 -
), calculando como IC = 1 - ![]() . O mais comum é definir o IC em 95%, significando que em uma amostra que segue distribuição normal, esses 95% representam +- 1,96 desvios da média.
. O mais comum é definir o IC em 95%, significando que em uma amostra que segue distribuição normal, esses 95% representam +- 1,96 desvios da média.
Exemplo com o pacote {infer} no R
Podemos realizar um exemplo utilizando o R. O código completo do exemplo e o vídeo comentado estão disponíveis para os membros do Clube AM.
Consideramos uma suposição: se uma pessoa boceja, é provável que ao presenciar o momento, uma outra pessoa boceja logo em seguida?
O dataset mithbuster_yawn representa os dados de uma pesquisa realizada por um episódio da série Mithbuster, em que uma pessoa bocejava em frente aos participantes, e realizava-se a anotação se os participantes bocejavam ou não em seguida.
É possível calcular a diferença de proporção entre aqueles que bocejaram e aqueles não bocejaram a partir da amostra. O resultado pode nos mostrar se essa suposição é verdadeira ou não. Entretanto, não iremos apenas estimar esse único ponto, vamos trabalhar com os possíveis valores estimados e construir um intervalo de confiança para os resultados.
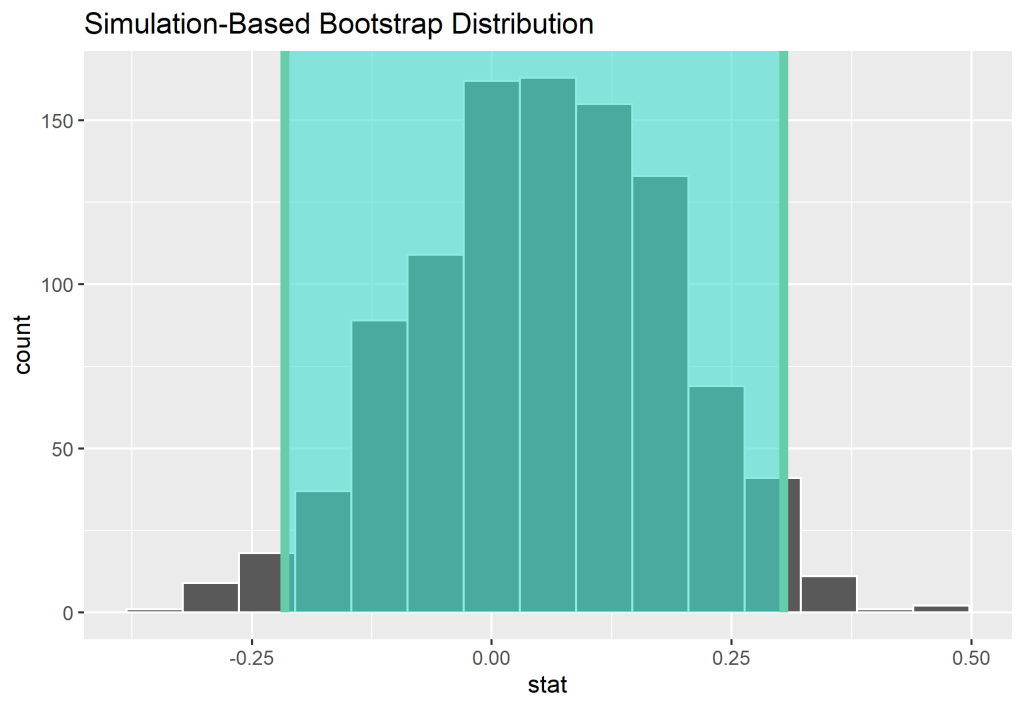
No R, calculamos a distribuição de pontos estimados através de uma simulação bootstrap repetindo o processo 1000 vezes. Com base nos valores obtidos, calculamos o intervalo de confiança em dois erros padrão de distância para cima e para baixo. A linha vertical representa o ponto estimado original, sem realizar a simulação de reamostragem.
Se esse procedimento é repetido 1000 vezes, então é esperado que em 950 vezes, o intervalo de confiança captura o verdadeiro valor da diferença de proporção entre aqueles que bocejaram e não bocejaram, enquanto os 50 restantes não.
Em outras palavras, definimos: Estamos 95% confiantes de que o verdadeiro valor da diferença de proporção entre aqueles que bocejaram e não bocejaram está entre (-0.216, 0.304).
A questão é: como sabemos se há diferença? Sabemos que o valor 0 é abrangido pelo intervalo de confiança. Se a diferença é igual a 0, sabemos que bocejar não há efeito.
Ao calcular o ponto estimado 1000 vezes através do método bootstrap, chegamos ao resultado de que o valor era tanto abaixo de 0, quanto acima de 0, o que sugere que não há evidencias de que há diferença no efeito de bocejar previamente antes de alguém bocejar em seguida.
Se os 95% de confiança estivessem acima de 0, poderíamos concluir que aqueles expostos pelo bocejo, bocejariam logo em seguida.
Faça parte do Clube AM!
Acesse o que há de mais moderno em scripts de R e Python para coletar, tratar, analisar e apresentar dados. Receba todos os exercícios produzidos diariamente na Análise Macro.
Quer saber mais?
Veja nossos cursos de R e Python aplicados para a Análise de Dados e Economia
- R para Análise de Dados
- Python para Análise de Dados
- Gráficos com ggplot2
- Estatística usando R e Python
- Machine Learning usando o R
_____________________________________________
Veja os post anteriores sobre o assunto
- Afinal, o que é Probabilidade?
- O que é Inferência Estatística?
- O que é Teste de Hipóteses
- Usando Bagging e Bootstrap no R
Referências
Kim, Y. Albert. Ismay, Chester. Statistical Inference via Data Science A ModernDive into R and the Tidyverse