Quem trabalha com previsões quantitativas sabe que uma parte importante de qualquer projeto é a avaliação das previsões geradas pelo(s) modelo(s). É dessa forma que podemos verificar se estamos no caminho correto. Para ilustrar como isso pode ser feito no R, vou construir nesse post um modelo univariado simples para a taxa de desemprego medida pela PNAD Contínua e depois efetuar o processo de avaliação das previsões geradas. Para começar, vamos carregar alguns pacotes...
library(forecast) library(ggplot2) library(sidrar) library(xtable)
Vamos pegar os dados que precisamos do SIDRA com o pacote sidrar...
# Dados Brutos table = get_sidra(api='/t/6318/n1/all/v/1641/p/all/c629/all') # Pegar a PEA pea = table$Valor[table$`Condição em relação à força de trabalho e condição de ocupação (Código)`==32386] # Pegar a População Desocupada desocupada = table$Valor[table$`Condição em relação à força de trabalho e condição de ocupação (Código)`==32446] # Criar Desemprego desemprego = ts(desocupada/pea*100, start=c(2012,03), freq=12)
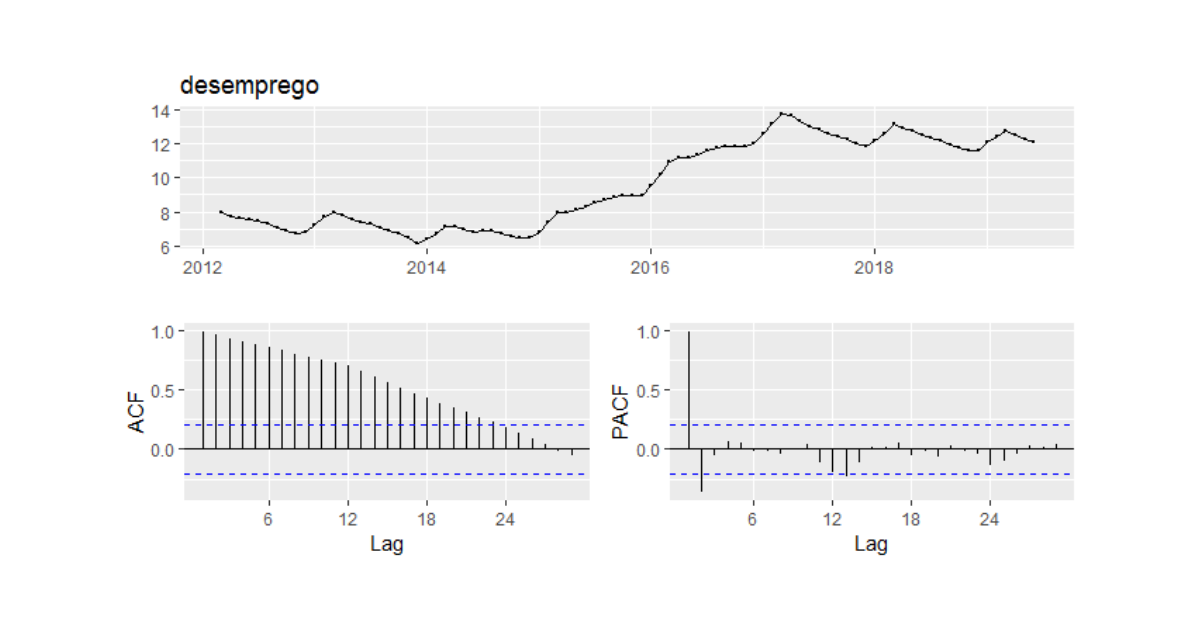
Com a função ggtsdisplay do pacote forecast podemos visualizar a nossa série e as funções de autocorrelação como abaixo.
Para a construção de um modelo univariado, teríamos que (1) verificar se a nossa série é estacionária e (2) tentar identificar os coeficientes AR e MA através de funções de autocorrelação. Vamos aqui, entretanto, utilizar um algoritmo de modo a automatizar esse processo através de critérios de informação com a função auto.arima:
sarima = auto.arima(desemprego, max.p=2, max.q=4, max.P = 2, max.Q=2)
Aplicada a função auto.arima sobre a nossa série, temos um modelo SARIMA(1,2,0)(1,1,0)[12]. Com base nesse modelo, podemos agora gerar previsões e, consequentemente, avaliá-las. É comum aqui, por suposto, dividir a nossa amostra em duas subamostras: uma de treino, onde rodamos o nosso modelo e outra de teste, onde são feitas as previsões. Nessa amostra de teste é onde ocorre a comparação com as observações efetivas da nossa série. Como regra de bolso, é comum destinar 70% para a subamostra de treino e o restante para a amostra de teste. Como nossa amostra é, entretanto, curta, vou aqui reservar apenas as 6 últimas observações para o conjunto de teste, de modo a ilustrar apenas o código.
training = window(desemprego, end=end(desemprego)-c(0,6)) test = window(desemprego, start=end(desemprego)-c(0,5)) acuracia = Arima(training, order=c(1,2,0), seasonal = c(1,1,0)) acuraciaf = forecast(acuracia, h=length(test), level=95)
Com o código acima, criamos as nossas subamostras, rodamos o modelo na subamostra de treino e gerar a previsão com base no tamanho do vetor de teste. Por fim, com a função accuracy do pacote forecast podemos avaliar essas previsões.
acc = accuracy(acuraciaf$mean, test)
E aí está a tabelinha que queríamos...
| ME | RMSE | MAE | MPE | MAPE | ACF1 | Theil's U | |
|---|---|---|---|---|---|---|---|
| Test set | -0.19 | 0.23 | 0.20 | -1.51 | 1.57 | 0.37 | 0.87 |
O erro médio do nosso modelinho é de 0,19 negativos e o RMSE é de 0,23. Para maiores detalhes sobre essas métricas, veja esse post aqui.
Curtiu o tema? Nós exploramos isso e muito mais no nosso Curso de Construção de Cenários e Previsões usando o R, voltado exclusivamente para a construção de previsões quantitativas no R. Dê uma olhada lá e se inscreva na próxima turma!