No Hackeando o R de hoje, mostraremos como capturar anomalias de séries temporais de forma rápida e simples. A grosso modo, essas anomalias nas séries aparecem quando eventos não esperados "distorcem" os seus valores, portanto, quando se trabalha com uma análise dos dados, é importante saber quais são esses valores e quando ocorreram, para isso, o pacote {anomalize} nos ajuda nessa tarefa.
O pacote por padrão utiliza o método STL (caso queira se aprofundar no assunto veja esse post), retirando os componentes de tendência e sazonalidade e evidenciando as anomalias.
Iremos utilizar dados de preços e retornos de ações como exemplo, importando-os do ano de 2020 até o dia de hoje. Caso queira saber mais sobre, veja esse post.
library(tidyquant) library(tidyverse) library(timetk) library(anomalize) library(tibbletime)
# Define os ativos que irão ser coletados
tickers <- c("PETR4.SA", "ITUB4.SA", "ABEV3.SA", "JBSS3.SA")
# Define a data de início da coleta
start <- "2019-12-01"
# Realiza a coleta dos preços diários
prices <- getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
from = start,
src = "yahoo") %>%
map(~Cl(get(.))) %>%
reduce(merge) %>%
`colnames<-`(tickers)
# Calcula os retornos mensais
asset_returns <- Return.calculate(prices,
method = "log") %>%
na.omit() %>%
tk_tbl(preserve_index = TRUE,
rename_index = "date")
# Transforma os dados em long
asset_returns_long <- asset_returns %>%
pivot_longer(!date, names_to = "asset", values_to = "value")
Com nossos dados em mãos, podemos utilizar as funções dos pacote. A primeira, time_decompose(), nos fornece a decomposição da série, nos retornando as colunas dos nossos dados atuais observados (observed), os valores da sazonalidade (season), tendência (trend), e o "restante", que são os valores dos dados observados menos a sazonalidade e tendência.
A segunda função, anomalize(), nos fornece a detecção de anomalias, examinando a coluna "remainder".
Por fim, utilizamos a função time_recompose() para calcular os outliers com base nos valores dos dados observados.
# Cria o tibble com valores dos componentes e da anomalia asset_anomalized <- asset_returns_long %>% group_by(asset) %>% time_decompose(value, merge = TRUE) %>% anomalize(remainder) %>% time_recompose()
Com os dados em mãos, podemos visualizar através da função plot_anomalies().
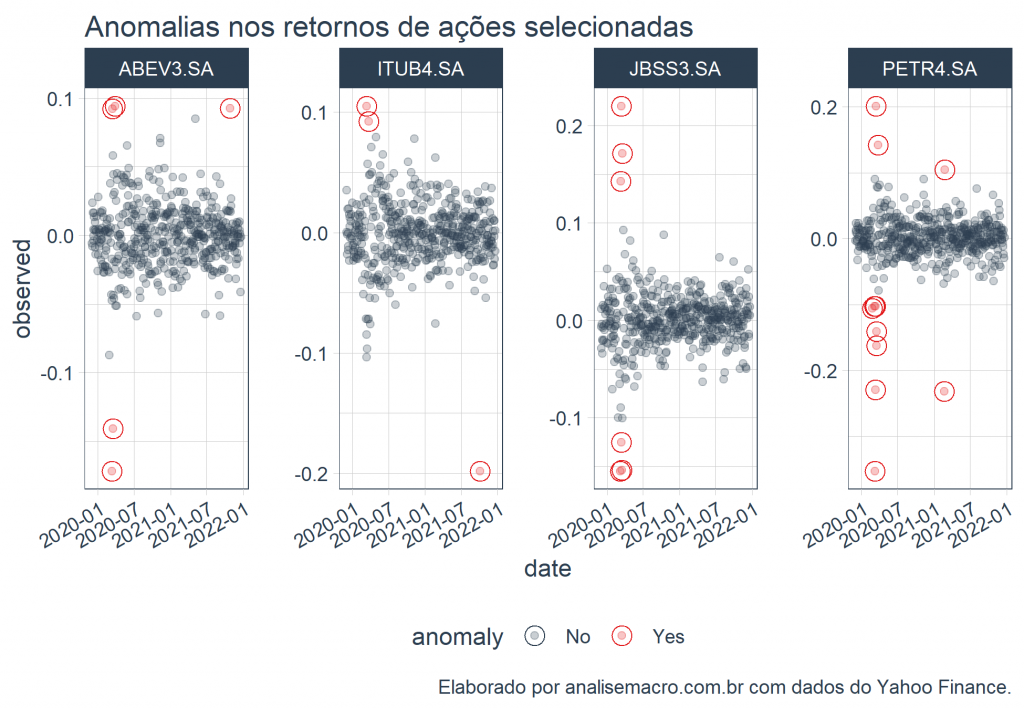
# Plota as anomalias dos retornos asset_anomalized %>% plot_anomalies(ncol = 4, alpha_dots = 0.25)+ ggplot2::labs(title = "Anomalias nos retornos de ações selecionadas", caption = "Elaborado por analisemacro.com.br com dados do Yahoo Finance.")
O que nos chama a atenção nas anomalias do nossos dados são as datas de maiores ocorrências, período do advento da pandemia de COVID-19 no Brasil.
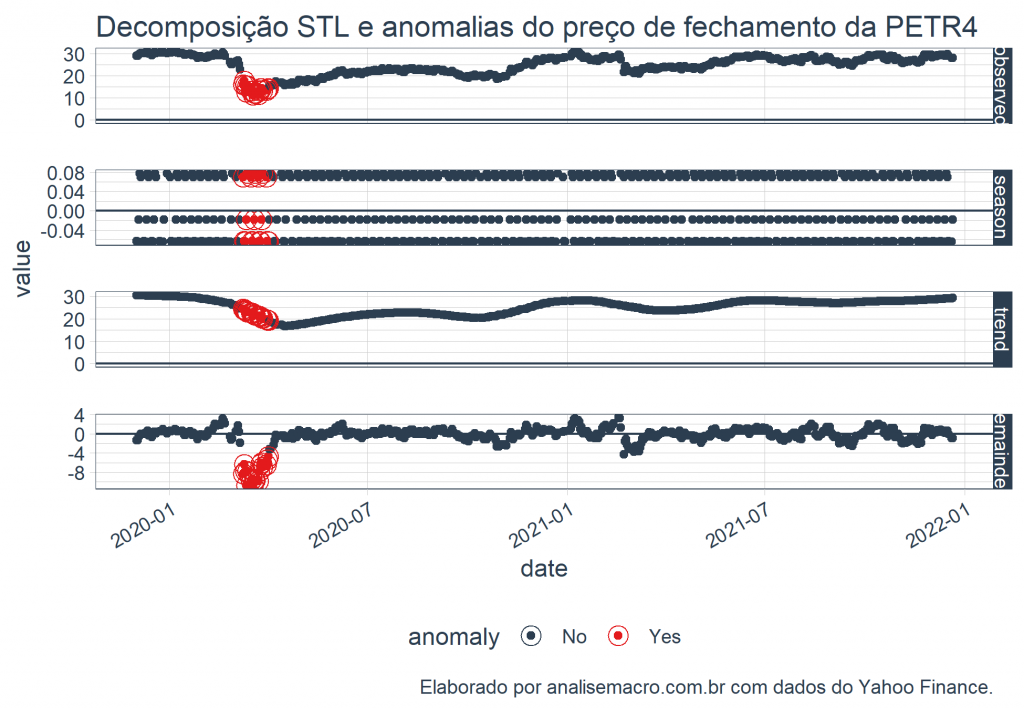
Podemos também verificar essas anomalias nos gráficos de decomposição. Como exemplo, utilizamos o ativo PETR4.
# Transforma em tibble petr4 <- prices %>% tk_tbl(preserve_index = TRUE, rename_index = "date") %>% select(date, petr4 = `PETR4.SA`) # Decompõe e calcula as anomalias petr4_anomalized <- petr4 %>% time_decompose(petr4) %>% anomalize(remainder) %>% time_recompose() # Plota a decomposição com as anomalias petr4_anomalized %>% plot_anomaly_decomposition()+ ggplot2::labs(title = "Decomposição STL e anomalias do preço de fechamento da PETR4", caption = "Elaborado por analisemacro.com.br com dados do Yahoo Finance.")
Vemos também as anormalidades em grande quantidade no mesmo período.
________________________
(*) Para entender mais sobre análise de séries temporais e mercado financeiro, confira nossos curso de Séries Temporais e Econometria Financeira.
________________________