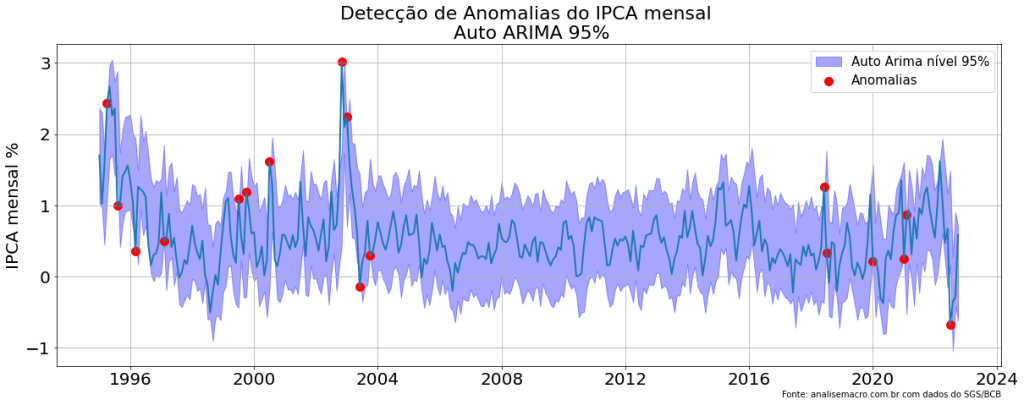
A detecção de anomalias em séries temporais permite identificar quebras estruturais devido a eventos não recorrentes na série analisada. No post de hoje, vamos aplicar a detecção de anomalias na série do IPCA mensal por meio de um Auto ARIMA usando a biblioteca statsforecast do Python.
Série Temporal e Anomalias
Um série temporal é uma sequência de observações que ocorrem de forma sucessiva em uma ordem do tempo, e no qual suas observações representam os valores de uma variável, ou seja, basicamente demonstra as mudanças nos valores de uma variável ao longo do tempo.
Séries temporais são comuns em séries financeiras e econômicas, portanto, ferramentas proporcionadas por essa área de estudo são bastante utilizadas para analisar e modelar essas séries.
Um dos problemas recorrente na analise de série temporais são problemas decorrentes de anomalias (também chamados de outliers). Anomalias são observações que não são usuais na série, ou seja, não seguem o padrão esperado.
Anomalias são picos ou quedas em um conjunto de dados de série temporal. A detecção de anomalias é o processo de identificar as anomalias em um conjunto de dados de séries temporais. O conjunto de dados de série temporal com anomalias leva a resultados inconsistentes durante a previsão.
IPCA Mensal
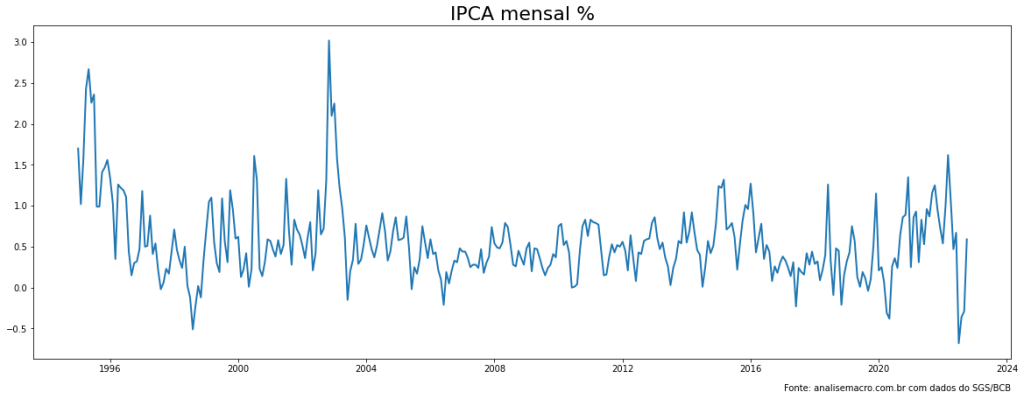
O IPCA Mensal refere-se a variação mensal do IPCA (índice de inflação do Brasil) e apresenta uma característica de ser centrada ao redor de um valor ao longo da série, bem como tem um padrão de variação, esses conceitos podem ser traduzidos de forma que o IPCA mensal seja estacionario. Vamos coletar os dados do IPCA mensal por meio do Sistema Gerenciador de Séries temporais do Banco Central e visualizar os valores ao longo do tempo (pegaremos dados somente após 1995 para evitar problemas com o anterior e de transição do real).
from bcb import sgs import matplotlib.pyplot as plt import numpy as np import pandas as pd from statsforecast import StatsForecast from statsforecast.models import AutoARIMA
# Coleta do IPCA
ipca_raw = sgs.get(('y', 433), start = '1995-01-01')
# Tratamento do IPCA
ipca = (
ipca_raw
.reset_index()
.assign(unique_id = 'ipca')
.rename(columns = {'Date' : 'ds' })
)
# Cria o gráfico
plt.figure(figsize = (20,7))
plt.plot(ipca['ds'], ipca['y'], linewidth = 2)
plt.title('IPCA mensal %', fontsize = 22)
# Adiciona a fonte no gráfico
plt.annotate('Fonte: analisemacro.com.br com dados do SGS/BCB',
xy = (1.0, -0.09),
xycoords='axes fraction',
ha='right',
va="center",
fontsize=10)
# Criação do modelo Auto ARIMA models = [AutoARIMA(season_length = 12, approximation = True)] fcst = StatsForecast(df = ipca, models = models, freq = 'M', n_jobs = -1)
# Nível de confiança do ajuste levels = [95] # Previsão dentro da amostra forecasts = fcst.forecast(h = 48, fitted = True, level = levels)
# Cria o ajuste insample_forecasts = fcst.forecast_fitted_values().reset_index()
# Cria o gráfico
fig,ax = plt.subplots(1,1,figsize = (20,7))
ax.plot(insample_forecasts['ds'], insample_forecasts['y'], linewidth = 2)
ax.fill_between(insample_forecasts['ds'],
insample_forecasts['AutoARIMA-lo-95'],
insample_forecasts['AutoARIMA-hi-95'],
alpha = .35,
color = 'blue',
label = 'Auto Arima nível 95%')
anomalies_df = insample_forecasts.query('y > `AutoARIMA-hi-95` or y < `AutoARIMA-lo-95`')[['ds', 'y']]
ax.scatter(
anomalies_df['ds'],
anomalies_df['y'],
color = 'red',
label = 'Anomalias',
s = 100
)
ax.set_title(f'Detecção de Anomalias do IPCA mensal \n Auto ARIMA 95%', fontsize=22)
ax.set_ylabel('IPCA mensal %', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid()
for label in (ax.get_xticklabels() + ax.get_yticklabels()):
label.set_fontsize(20)
# Adiciona a fonte no gráfico
plt.annotate('Fonte: analisemacro.com.br com dados do SGS/BCB',
xy = (1.0, -0.09),
xycoords='axes fraction',
ha='right',
va="center",
fontsize=10)
________________________________________________
Quer se aprofundar no assunto?
Alunos da trilha de Ciência de dados para Economia e Finanças possuem acesso o curso Analise de dados Macroeconômicos e Financeiros e podem aprender a como construir projetos que envolvem dados reais usando modelos econométricos e de Machine Learning com o R.