Mínimos Quadrados em 2 Estágios (TSLS)

Neste artigo compreenderemos o que é o Mínimo Quadrados em 2 Estágios, a sua contribuição para a econometria e macroeconomia e a possibilidade de utilizar essa ferramenta usando o Python.

Observe que podemos assumir que os termos de erro no modelo de regressão linear são contemporaneamente não correlacionados com as variáveis explanatórias, ou mesmo que eles seriam independentes de todas as variáveis explanatórias.

Lembre-se que independência é uma hipótese mais forte do que ausência de correlação. Com efeito, poderíamos interpretar o modelo de regressão linear como descrevendo a expectativa condicional de $y_t$ , dado um conjunto de variáveis $x_t$ .

Vamos ver o caso onde não podemos assumir exogeneidade das variáveis explanatórias, o que implica que os estimadores de MQO serão viesados e inconsistentes. De forma a ilustrar, considere o modelo descrito por

(1) $\begin{align*} y_i = x_i^{'} \beta + \varepsilon_i, \nonumber \end{align*}$

que pode ser descrito como

(2) $\begin{align*} y = X \beta + \varepsilon \nonumber \end{align*}$

$b$ é um estimador de MQO não viesado para $\beta$ se estamos assumindo que $\varepsilon$ possui média zero, dado $X$ , isto é, $E\left \{ \varepsilon|X \right \} = 0$ . Isso implica que o conhecimento sobre qualquer uma das variáveis explanatórias não informa nada sobre o valor esperado dos termos de erro. Independência de $X$ em relação $\varepsilon$ com $E\left \{ \varepsilon \right \} = 0$ implica que $E\left \{ \varepsilon|X \right \} = 0$ , mas é ainda mais forte, dado que implica que a variância de $\varepsilon$ também não depende de $X$ .

Em muitos casos, a hipótese de que $\varepsilon$ é independente de $X$ é muito forte. Como exemplo, considere a hipótese de mercados eficientes, sob retornos esperados constantes. Essa hipótese implica que o retorno de qualquer ativo será imprevisível a partir de informações públicas. Sob sua forma fraca, o retorno de ativos não pode ser previsto a partir dos retornos passados. A hipótese pode ser, aliás, estatisticamente testada, considerando um modelo de regressão linear e testando se os retornos passados explicam o retorno presente.

Isto é,

(3) $\begin{align*} y_t = \beta_1 + \beta_2 y\_{t-1} + \beta_3 y\_{t-2} + \varepsilon_t, \end{align*}$

onde $y_t$ denota o retorno no período $t$ , a hipótese nula implica que $\beta_2 = \beta_3 = 0$ . Dado que as variáveis explanatórias são variáveis defasadas (sendo assim função dos termos de erro defasados), a premissa de que $E\left \{ \varepsilon|X \right \} = 0$ é inapropriada. Se a autocorrelação nos termos de erro for, de algum modo, restringida, será ainda possível fazer inferência de modo apropriado, utilizando a estimativa de Newey-West para a matriz de covariância.

Observe, ademais, que mesmo que consideremos a hipótese de que $E\left \{ \varepsilon_t x_t\right \} = 0$ , isto é, que os termos de erro e as variáveis explanatórias não são contemporaneamente correlacionadas, haverá casos em que isso não será necessariamente válido. Para esses, não mais poderemos dizer que o estimador de MQO será não viesado e consistente. Exemplos desses casos são: presença de variáveis dependentes defasadas e correlacionadas com o termo de erro, erros de medida e simultaneidade ou endogeneidade dos regressores. Vamos tratar a seguir do último e mais interessante caso.

Endogeneidade e viés de variável omitida

O problema de viés gerado por variável omitida aparece se uma variável explanatória relevante, correlacionada com os regressores incluídos, é omitida do modelo. Implicitamente, isso assume que o conjunto de variáveis explanatórias é maior do que aquele descrito no lado direito da equação estimada. O viés de variável omitida também aparece se existe um fator não observado que está sendo omitido do modelo que também é correlacionado com uma ou mais variáveis explicativas. Esse viés é particularmente preocupante quando estamos interessados em fazer uma interpretação causal dos nossos coeficientes estimados, o que nesse caso implica em levar em consideração a hipótese de ceteris paribus.

Obs. A presença de um componente não observado na equação que é potencialmente correlacionado com os regressores é também referido na literatura como heterogeneidade não observada.

Para ilustrar, considere uma equação de salários individuais, especificada como

(4) $\begin{align*} y_i = x\_{1i}^{'} \beta_1 + x\_{2i} \beta_2 + u_i \gamma + v_i, \end{align*}$

onde, $y_i$ é o salário em $log$ de um determinado indivíduo, $x_{1i}$ é um vetor de características individuais, incluindo o intercepto e $x_{2i}$ denota anos de escolaridade. Ademais, $u_i$ é uma variável não observado que reflete a habilidade de um determinado indivíduo. Pessoas com níveis elevados de habilidade tendem a possuir salários mais altos $(\gamma > 0)$ , mas também mais prováveis de terem maior escolaridade.

Assim, podemos esperar que $cov\left \{ x_{2i}, u_i \right \} > 0$ . Dado que $u_i$ é não observado, o econometrista irá estimar

(5) $\begin{align*} y_i = x_i^{'} \beta + \varepsilon_i, \end{align*}$

onde $x_i^{'} = (x_{1i}^{'}, x_{2i}^)$ , $\beta^{'} = (\beta_{1}^{'}, \beta_2)$ e $\varepsilon_i = u_i \gamma + v_i$ . É possível mostrar ainda que o estimador de MQO para $\beta$ satisfaz

(6) $\begin{align*} b = \beta + (\sum\_{i=1}\^{N} x\_{i}x\_{i}^{'})\^{-1} \sum\_{i=1}\^{N} x\_{i} u\_{i} \gamma + (\sum\_{i=1}\^{N} x\_{i}x\_{i}^{'})\^{-1} \sum\_{i=1}\^{N} x\_{i} v\_{i}. \end{align*}$

Assumindo $E\left \{ x_i v_i \right \} = 0$ , isso nos permite mostrar que o limite de probabilidade para $b$ é dado por

(7) $\begin{align*} plim b = \beta + \sum\_{xx}\^{-1} E \left \{ x_i u_i \right \} \gamma. \end{align*}$

Portanto, quando $\gamma \neq 0$ , a consistência do estimador de MQO requer $E \left \{ x_i u_i \right \} = 0$ . Isto é, a habilidade não observada deveria ser não correlacionada com a escolaridade e as demais variáveis do modelo.

Assumindo $E \left \{ x_i u_i \right \} > 0$ , espera-se que o MQO superestime o retorno da escolaridade. Qual será a estimativa de MQO nesse caso? Ela dirá o quanto o salário esperado de duas pessoas diferirá se uma tem 1 ano a mais de escolaridade do que outra, mantidos valores iguais para $x_{1i}$ . Isso não é um efeito causal. Isso apenas diz que pessoas com maior educação esperam ter um salário maior. Parte desse efeito pode ser atribuído ao fato de que pessoas com diferentes anos de escolaridade também possuem diferentes características não observadas (habilidade, ambição, inteligência, etc.). O diferencial salarial que é causado pela diferença de escolaridade (isto é, o efeito de $x_{2i}$ , mantidos $x_{1i}$ e $u_i$ fixos) pode ser de fato bem menor do que a estimativa produzida por MQO.

De modo geral, variáveis explanatórias em $x_i$ que são correlacionadas com o termo de erro $\varepsilon_i$ são chamadas de endógenas. As que não são correlacionadas são tidas como exógenas.

Simultaneidade e causalidade reversa

Uma outra forma do problema de endogeneidade é a causalidade reversa. Isto é, não apenas $x_i$ possui impacto sobre $y_i$ , como ao mesmo tempo $y_i$ tem impacto sobre um ou mais elementos de $x_i$ , como $x_{2i}$ . Por exemplo, o nível de criminalidade em uma determinada cidade será afetada pelo quantidade de dinheiro gasto no cumprimento da lei, enquanto funcionários públicos podem decidir aumentar o orçamento da segurança em função do nível esperado de criminalidade. Estimar o impacto causal da aplicação da lei sobre o nível de criminalidade usando uma amostra de corte transversal estará assim sujeito ao viés de endogeneidade.

A situação de causalidade reversa naturalmente aparece quando $y$ e $x_2$ são determinados simultaneamente. Em macroeconomia, por exemplo, há um número grande de modelos que consiste em um sistema de equações que simultaneamente determina um número de variáveis endógenas. Considere, por exemplo, uma equação de demanda e outra de oferta, ambas dependentes dos preços, e uma condição de equilíbrio que diga oferta e demanda são iguais. O sistema de equações resultante simultaneamente determina quantidade e preços, de modo que não podemos afirmar que preços determinam quantidades ou que quantidades determinam preços.

Para ilustrar, considere um exemplo simples de \textbf{modelo de equações simultâneas}. A equação de interesse é uma função de consumo keynesiana que relaciona o consumo per capita $y_t$ de um país à renda per capita $x_{2t}$ dada por

(8) $\begin{align*} y_t = \beta_1 + \beta_2 x_{2t} + \varepsilon_t, \end{align*}$

onde $t = 1,...,T$ . O coeficiente $\beta_2$ é interpretado como a propensão marginal a consumir, e espera-se que esteja no intervalo entre 0 e 1. Isso é uma interpretação causal que descreve o impacto da renda sobre o consumo: quanto mais as pessoas irão consumir se sua renda aumentar em uma unidade? Entretanto, a renda agregada $x_{2t}$ não é exógena dado que será determinada pela identidade

(9) $\begin{align*} x_{2t} = y_t + z_{2t} \end{align*}$

onde $z_{2t}$ representa o investimento per capita.

Essa equação é uma equação de definição para uma economia fechada sem governo. Ela diz que o total consumido mais o investimento deve ser igual à renda. Nós assumimos que o investimento é exógeno, o que significa que $z_{2t}$ e $\varepsilon_t$ não são correlacionados, isto é,

(10) $\begin{align*} E \left \{ z_{2t} \varepsilon_t \right \} = 0. \end{align*}$

Isto significa que $z_{2t}$ é determinado fora do modelo. Em contraste, tanto $y_t$ quanto $x_{2t}$ são variáveis endógenas, determinadas conjuntamente dentro do modelo. O modelo em 8 e 9 é um modelo de equações simultâneas simples da \textbf{forma estrutural}.

Esse modelo simples ilustra um problema comum em modelos macro ou microeconômicos. Se considerarmos uma equação onde um ou mais variáveis explanatórias são determinadas conjuntamente com a variável do lado esquerdo (a variável independente), o estimador de MQO proverá estimativas inconsistentes para os parâmetros comportamentais. Estatisticamente, isso significa que a equação que escrevemos não corresponde à expectativa condicional de modo que as premissas usuais sobre o termo de erro não podem ser impostas.

Variáveis instrumentais em modelos de regressão simples

De forma a contornar o problema da endogeneidade, podemos deixar a variável não observada no termo de erro, mas ao invés de estimar o modelo por MQO, nós fazemos uso de um método de estimação que reconhece a presença da variável omitida. É basicamente isso que o método de variáveis instrumentais faz. Variáveis instrumentais são, a propósito, uma poderosa ferramenta para identificar e estimar relações causais.

Para ilustrar, considere o modelo simples de regressão linear abaixo especificado

(11) $\begin{align*} y = \beta_0 + \beta_1 x + u \end{align*}$

O estimador de MQO para o parâmetro de inclinação é dado por

(12) $\begin{align*} \hat{\beta}\_1\^{MQO} = \frac{Cov(x,y)}{Var(x)} \end{align*}$

Se supormos, por suposto, que o regressor $x$ é correlacionado com o termo de erro $u$ , esse estimador será viesado e inconsistente.

Se tivermos um instrumento válido $z$ , nós podemos estimar $\beta_1$ de forma consistente usando o estimador de variáveis instrumentais

(13) $\begin{align*} \hat{\beta}_1^{IV} = \frac{Cov(z,y)}{Cov(z,x)} \end{align*}$

Isto é, um instrumento válido é correlacionado com o regressor $x$ , o que implica que o denominador de 13 é diferente de zero. Ele também deve ser não correlacionado como o termo de erro $u$ .

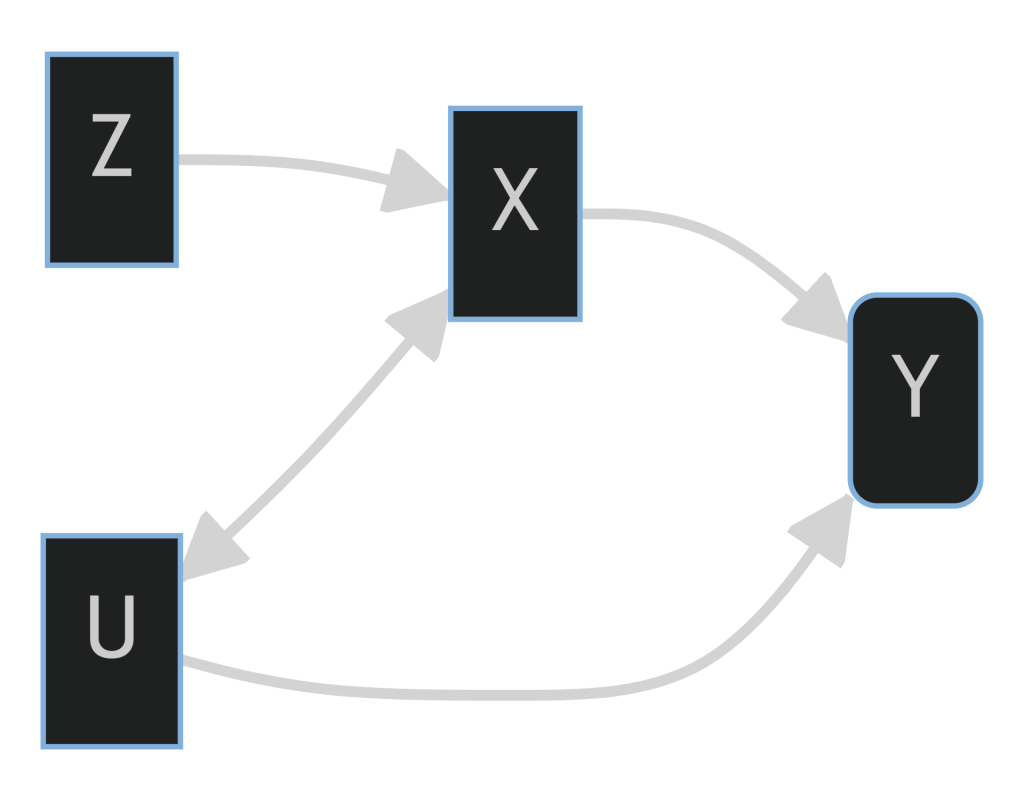
Na figura abaixo, é exposto a explicação anterior, identificando a relação entre os termos.

Variáveis instrumentais em modelos de regressão simples usando o Python

Para ilustrar a implementação de variáveis instrumentais no `Python`, vamos considerar o Exemplo 15.1 de Wooldridge, sobre o retorno da educação para mulheres casadas.

Para obter todo o código em Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

Utilizamos os dados sobre mulheres casadas que trabalham contidos no dataset`mroz`, importado via a biblioteca `linearmodels` para estimar o retorno da educação no modelo de regressão simples

(14) $\begin{align*} ln(\text{salário}\_h) = \beta_0 + \beta_1 \text{educ} + u \end{align*}$

Como ferramenta para estimar as regressões utilizaremos o `linearmodels` para o Mínimos Quadrados usual e para o Mínimos Quadrados em 2 Estágios.

   inlf  hours  kidslt6  kidsge6  age  educ    wage  repwage  hushrs  husage  \
0     1   1610        1        0   32    12  3.3540     2.65    2708      34   
1     1   1656        0        2   30    12  1.3889     2.65    2310      30   
2     1   1980        1        3   35    12  4.5455     4.04    3072      40   
3     1    456        0        3   34    12  1.0965     3.25    1920      53   
4     1   1568        1        2   31    14  4.5918     3.60    2000      32   

   ...  faminc     mtr  motheduc  fatheduc  unem  city  exper   nwifeinc  \
0  ...   16310  0.7215        12         7   5.0     0     14  10.910060   
1  ...   21800  0.6615         7         7  11.0     1      5  19.499980   
2  ...   21040  0.6915        12         7   5.0     0     15  12.039910   
3  ...    7300  0.7815         7         7   5.0     0      6   6.799996   
4  ...   27300  0.6215        12        14   9.5     1      7  20.100060   

      lwage  expersq  
0  1.210154      196  
1  0.328512       25  
2  1.514138      225  
3  0.092123       36  
4  1.524272       49  

[5 rows x 22 columns]

Como o MQO (OLS) é um caso especial do MQO em dois estágios (2SLS), o módulo IV2SLS pode ser usado para estimar um modelo usando OLS, definindo as variáveis endógenas (endog) e instrumentais (instruments).

É possível utilizar o próprio módulo IV2SLS e seus respectivos parâmetros ou o método from_formula, que permite expressar a especificação. Temos então o logaritmo da variável wage em função de uma constante 1 e do regressor educ.

Temos, portanto, na especificação, em que educ é o regressor e fatheduc é o instrumento.

É possível, portanto, comparar ambos os modelos. Vemos que no caso de variáveis instrumentais, o coeficiente de educ é menor, ou seja, o seu efeito é menor se adicionado fatheduc.

Código

                   Model Comparison                   
======================================================
                                  OLS             2SLS
------------------------------------------------------
Dep. Variable            np.log(wage)     np.log(wage)
Estimator                         OLS          IV-2SLS
No. Observations                  428              428
Cov. Est.                  unadjusted       unadjusted
R-squared                      0.1179           0.0934
Adj. R-squared                 0.1158           0.0913
F-statistic                    57.196           2.8487
P-value (F-stat)            3.941e-14           0.0914
==================     ==============   ==============
Intercept                     -0.1852           0.4411
                            (-1.0022)         (0.9911)
educ                           0.1086           0.0592
                             (7.5628)         (1.6878)
==================== ================ ================
Instruments                                   fatheduc
------------------------------------------------------

T-stats reported in parentheses

Estimação de variáveis instrumentais em modelos de regressão múltipla

O método de variáveis instrumentais pode ser facilmente generalizado de modo a incluir variáveis exógenas adicionais, isto é, regressores que são assumidos serem não correlacionados com o termo de erro. Na função IV2SLS, nós temos de adicionar essas variáveis tanto na lista de regressores quando na lista de instrumentos.

Para ilustrar a aplicação no Python, vamos considerar o Exemplo 15.4 de Wooldridge, sobre como utilizar a proximidade da faculdade como uma variável instrumental da educação.

Utilizamos os dados do dataset card de modo a estimar o retorno da educação. A educação é permitida para ser endógena e instrumentalizada com a variável dummy nearc4 que indica se o indivíduo cresceu próximo à faculdade. Ademais, são adicionadas variáveis de controle para experiência, raça e informação regional. Essas variáveis são supostamente exógenas, de modo que são instrumentalizadas por elas mesmas.

A tabela a seguir mostra os resultados para alguns dos parâmetros estimados.

Código

                           Model Comparison                          
=====================================================================
                                OLS          Log OLS             2SLS
---------------------------------------------------------------------
Dep. Variable                  wage     np.log(wage)     np.log(wage)
Estimator                       OLS              OLS          IV-2SLS
No. Observations               3010             3010             3010
Cov. Est.                unadjusted       unadjusted       unadjusted
R-squared                    0.1683           0.1932           0.2382
Adj. R-squared               0.1644           0.1895           0.2343
F-statistic                  609.04           720.93           769.20
P-value (F-stat)             0.0000           0.0000           0.0000
==================     ============   ==============   ==============
Intercept                    336.38           5.8760           3.6662
                           (11.522)         (121.09)         (3.9747)
exper                        33.019           0.0540           0.1083
                           (7.9297)         (7.8041)         (4.5886)
expersq                     -1.3339          -0.0022          -0.0023
                          (-6.5412)        (-6.5615)        (-7.0201)
black                       -141.64          -0.2677          -0.1468
                          (-12.243)        (-13.920)        (-2.7304)
smsa                         91.575           0.1687           0.1118
                           (7.0938)         (7.8617)         (3.5407)
south                       -75.054          -0.1523          -0.1447
                          (-4.4856)        (-5.4749)        (-5.3165)
smsa66                       24.313           0.0364           0.0185
                           (1.9417)         (1.7478)         (0.8599)
reg662                       62.068           0.0906           0.1008
                           (2.6846)         (2.3570)         (2.6810)
reg663                       79.595           0.1397           0.1483
                           (3.5185)         (3.7139)         (4.0380)
reg664                       29.729           0.0619           0.0499
                           (1.1081)         (1.3877)         (1.1438)
reg665                       55.883           0.1040           0.1463
                           (2.0745)         (2.3234)         (3.1162)
reg666                       59.714           0.1111           0.1629
                           (2.0500)         (2.2943)         (3.1466)
reg667                       52.722           0.0962           0.1346
                           (1.8276)         (2.0055)         (2.7313)
reg668                      -18.901          -0.0214          -0.0831
                          (-0.5728)        (-0.3903)        (-1.4040)
reg669                       90.388           0.1327           0.1078
                           (3.6147)         (3.1929)         (2.5853)
educ                                                           0.1315
                                                             (2.3989)
==================== ============== ================ ================
Instruments                                                    nearc4
---------------------------------------------------------------------

T-stats reported in parentheses

Mínimos Quadrados em Dois Estágios

Mínimos Quadrados em Dois Estágios (TSLS ou 2SLS, em inglês) é uma abordagem geral para estimativas via variável instrumental quando nós temos um ou mais regressores endógenos. De forma a ilustrar, considere o modelo

(15) $\begin{align*} y_1 = \beta_0 + \beta_1 y_2 + \beta_2 y_3 + \beta_3 z_1 + \beta_4 z_2 + \beta_5 z_3 + u_1 \end{align*}$

Os regressores $y_2$ e $y_3$ são potencialmente correlacionados com o termo de erro $u_1$ , enquanto que os regressores $z_1$ , $z_2$ e $z_3$ são tidos como exógenos. Dado que nós temos dois regressores endógenos, nós precisamos de ao menos dois instrumentos adicionais, vamos dizer $z_4$ e $z_5$ .

O nome TSLS vem do fato de que a regressão por MQO é performada em dois estágios:

1. Separadamente, regredisse $y_2$ e $y_3$ contra $z_1$ até $z_5$ , obtendo $\hat{y_2}$ e $\hat{y_3}$ ;
2. Regredisse $y_1$ contra $\hat{y_2}$ , $\hat{y_3}$ e $z_1$ até $z_3$ .

Se os instrumentos forem válidos, isso levará a estimativas consistentes dos parâmetros $\beta_0$ até $\beta_5$ .

O procedimento resumido acima está implementado na função `IV2SLS` da biblioteca `linearmodels`, que vimos no exemplos anteriores.

_____________________________________
Quer aprender mais?

Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.

________________________________________________

Referências

Wooldridge, J. M. 2013. Introductory Econometrics: A Modern Approach. Editora Cengage.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise de impacto fiscal sobre o dolár com Python

Resultado IBC-br - Outubro/2024

Resultado PMC - Outubro/2024

Como usar Inteligência Artificial para Ler as Atas do COPOM?

Resultado PMS - Outubro/2024

Resultado IPCA - Novembro/2024

Outros artigos relacionados

Análise de impacto fiscal sobre o dolár com Python

Usamos uma cesta de 12 moedas para construir um cenário contrafactual da taxa de câmbio após o último anúncio de pacote fiscal, com base em modelagem Bayesiana. No período, o dolár depreciou quase 5% e passou os R$ 6,15, enquanto que na ausência da intervenção a moeda deveria estar cotada em R$ 5,78.

Resultado IBC-br - Outubro/2024

A Análise Macro apresenta os resultados da IBC-br de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PMC - Outubro/2024

A Análise Macro apresenta os resultados da PMC de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Mínimos Quadrados em 2 Estágios (TSLS)

Endogeneidade e viés de variável omitida

Simultaneidade e causalidade reversa

Variáveis instrumentais em modelos de regressão simples

Variáveis instrumentais em modelos de regressão simples usando o Python

Estimação de variáveis instrumentais em modelos de regressão múltipla

Mínimos Quadrados em Dois Estágios

_____________________________________ Quer aprender mais?

Referências

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Outros artigos relacionados

Boletim AM

Boletim AM

_____________________________________
Quer aprender mais?