No post de hoje, vamos abordar os modelos lineares univariados, apresentando conceitos importantes por meio de simulações e gráficos criados por meio das linguagens R e Python. Nosso objetivo é proporcionar uma compreensão clara e acessível desses modelos, de modo que seja fácil de entender e acompanhar.
Para obter todo o código do processo de criação dos gráficos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Introdução aos modelos lineares univariados
Há, basicamente, duas formas de se entender uma série temporal, do ponto de vista econométrico. Modelos de série temporal podem ser:
- Modelos Univariados: as características da série de interesse são explicadas exclusivamente a partir do comportamento da própria série;
- Modelos Multivariados: as características da série de interesse são explicadas não apenas em função da própria série, mas também por outras séries. Os modelos multivariados podem ser escalares, quando há apenas uma única equação, ou vetoriais, quando há múltiplas equações.
Quando se utilizará uma ou outra forma de modelagem vai depender muito das características da nossa série de interesse, como veremos ao longo do nosso curso. Em termos simples, o objetivo da econometria de séries temporais univariada é encontrar a dependência dinâmica de uma série , isto é, a dependência de
em relação aos seus valores passados (
).
Focaremos nos modelos univariados lineares, onde depende linearmente dos seus valores passados, como abaixo:
(1)
Como veremos, modelos univariados podem ser uma boa forma de gerar previsões simples e rápidas para séries que, a priori, nós não temos maiores informações sobre variáveis exógenas que podem influenciar o seu comportamento.
Nesse contexto, para termos condições de modelar e gerar previsões nessa abordagem, vamos ver alguns conceitos básicos e importantes para prosseguirmos. Aprenderemos a analisar as famosas funções de autocorrelação, reconheceremos os termos AR e MA de um processo ARMA, aprenderemos a identificar o problema da não estacionariedade.
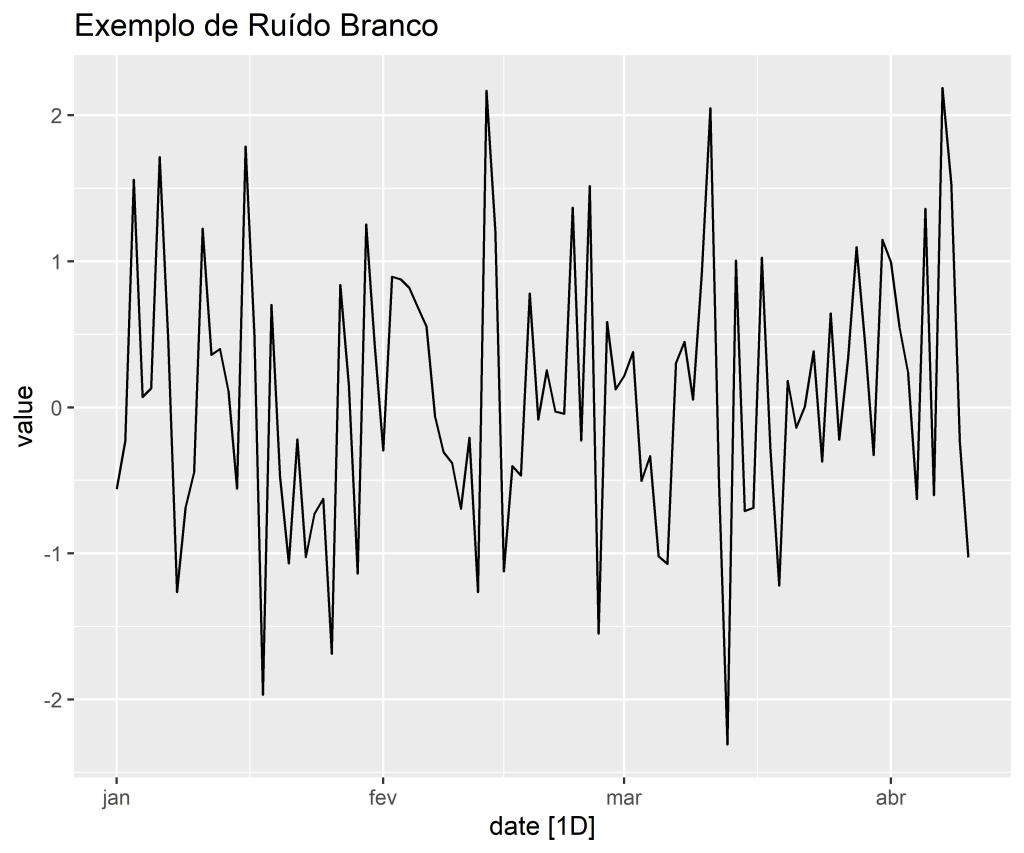
Ruído branco
Suporemos que os resíduos dos nossos modelos, isto é, a diferença entre os valores observados e aqueles preditos,
(2)
são o que chamamos na literatura de ruídos brancos porque consideraremos que
(3)
Em outras palavras, uma série qualquer, e não apenas os resíduos, será considerada um ruído branco se
forem independentes e identicamente distribuídos com média igual a zero e variância constante. Assumindo covariância igual a zero, temos, ademais, um ruído branco Gaussiano. Estamos assumindo, claro, uma distribuição normal.
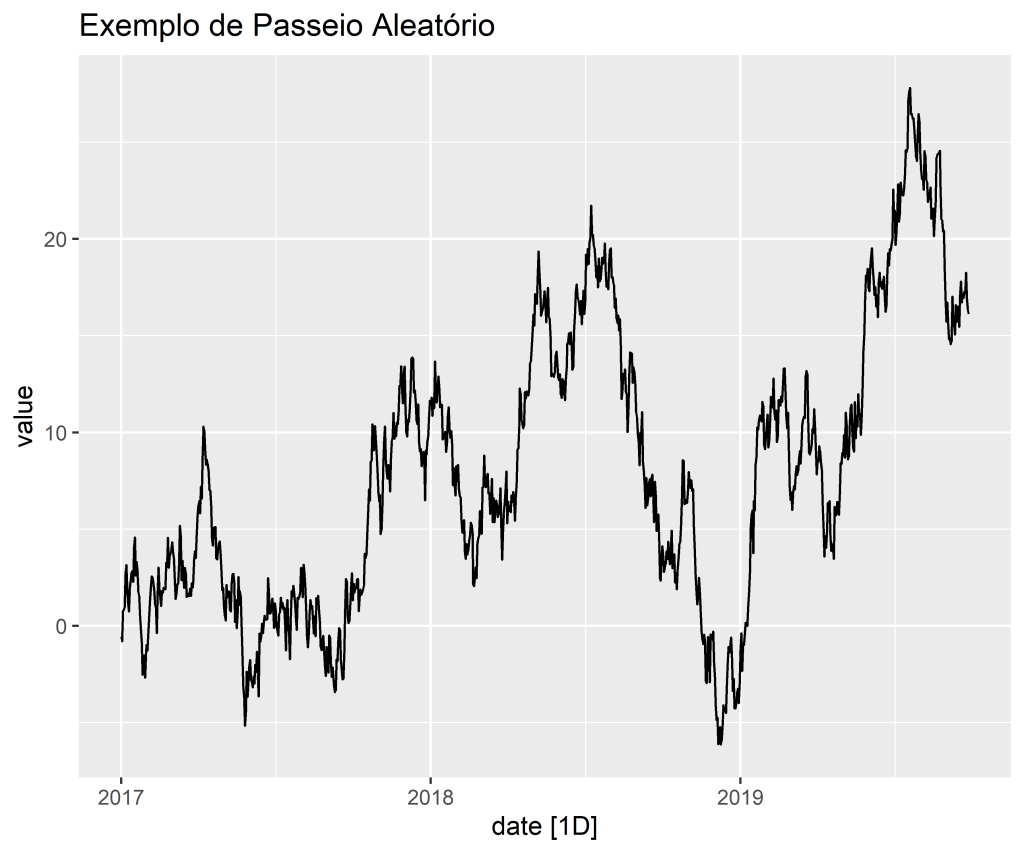
Passeio aleatório
Suponha que uma série possa ser modelada como
(4)
Onde segue um ruído branco. Substituindo
na equação acima e depois substituindo por
,
e assim por diante, temos:
(5)
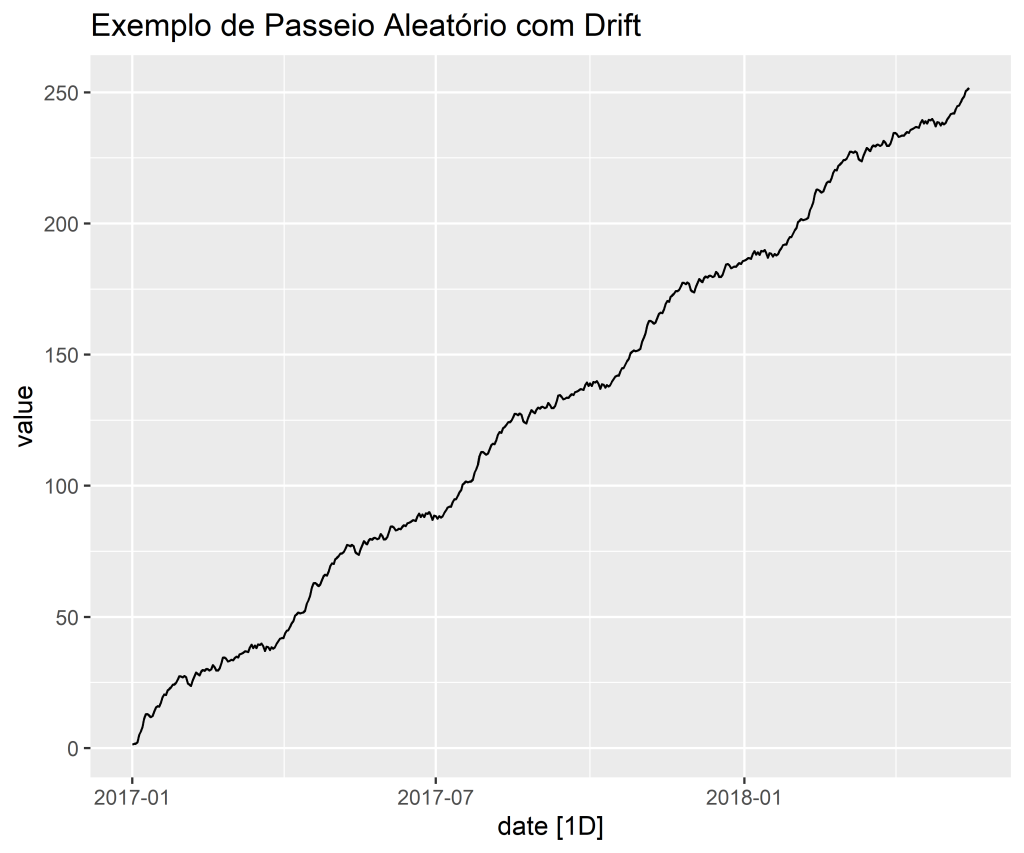
Observe, leitor, que a diferença entre um ruído branco e um passeio aleatório com ou sem drift é que o primeiro é uma série estacionária, no sentido discutido na seção anterior e o segundo, não. A estacionariedade será um conceito extremamente importante na hora de modelarmos a nossa série. Isto porque, é muito mais fácil modelar uma série com média e variância constantes do que uma série onde esses momentos são dependentes do tempo.
Modelos lineares univariados
Estaremos interessados em modelos que possam ser representados da forma
(7)
Onde é um ruído branco. Para o caso em que
, teremos modelos como
(8)
Onde quem irá dizer se o processo é ou não estacionário será o valor de
: (i) se
, o processo é estacionário; (ii) se
, o processo será não estacionário.
Funções de autocorrelação
Vimos anteriormente que uma série será estacionária se sua média e todas as suas autocovariâncias não são afetadas por mudanças na origem do tempo. A média, como vimos, será o valor esperado, , de
, que supomos ser igual a
. Fazendo
, teremos a média dos desvios quadrados ao redor de
, também conhecido como variância
de
. A covariância de
, aqui chamada de autocovariância, já que se refere a mesma série, será então dada por
, com
representando a defasagem da série temporal que estamos lidando. Para uma série covariância estacionária, nós podemos definir uma Função de Autocovariância como
(9)
Onde naturalmente não depende de
, dado que o valor esperado será o mesmo, independente de
. Assim, a Função de Autocorrelação, denominada como FAC (português) ou ACF (inglês) para uma defasagem
qualquer será dada por
(10)
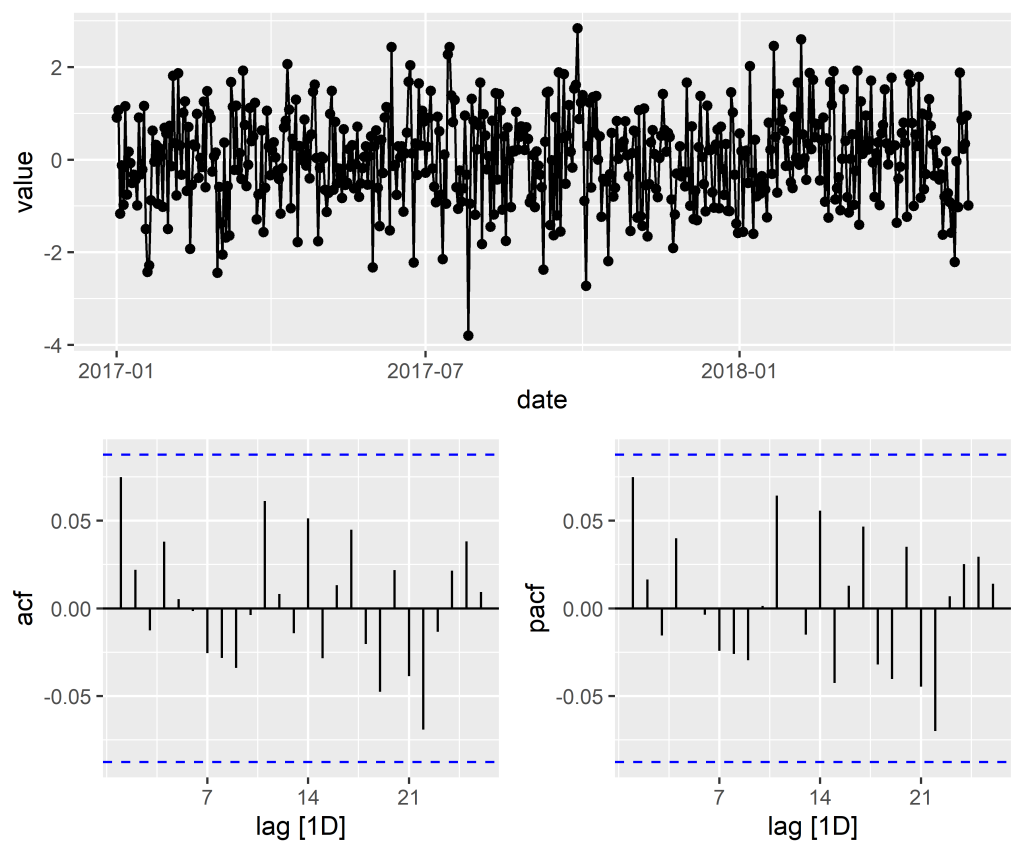
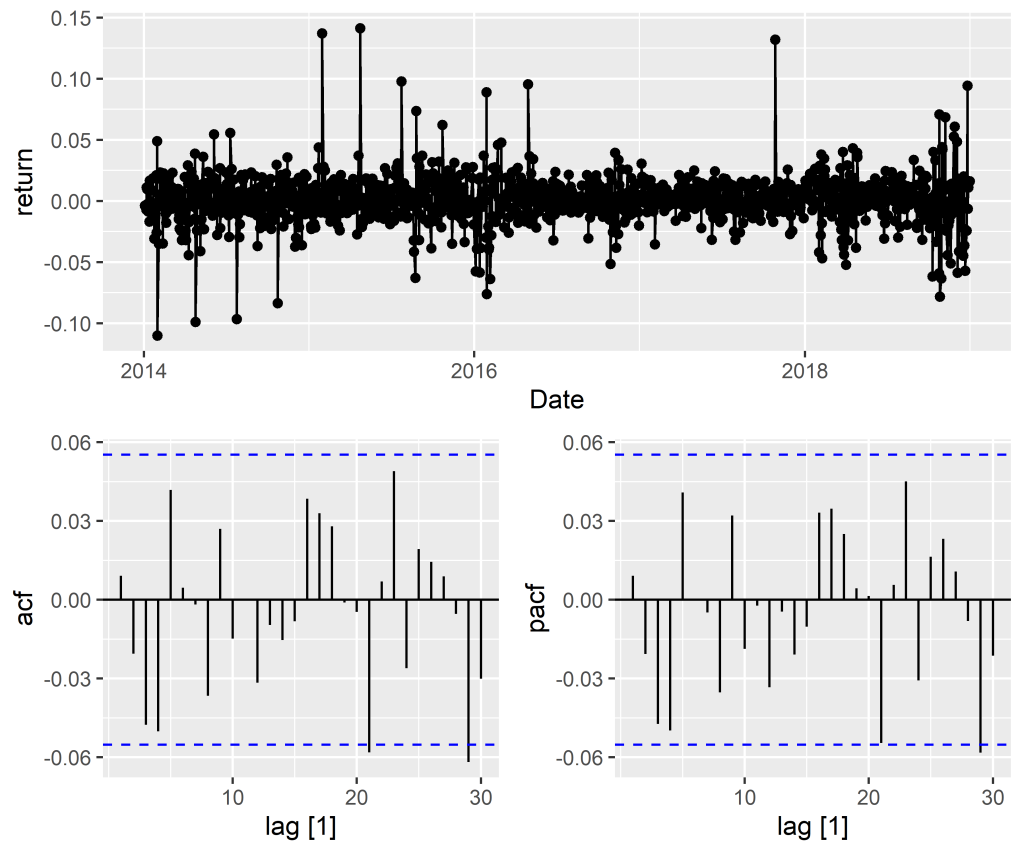
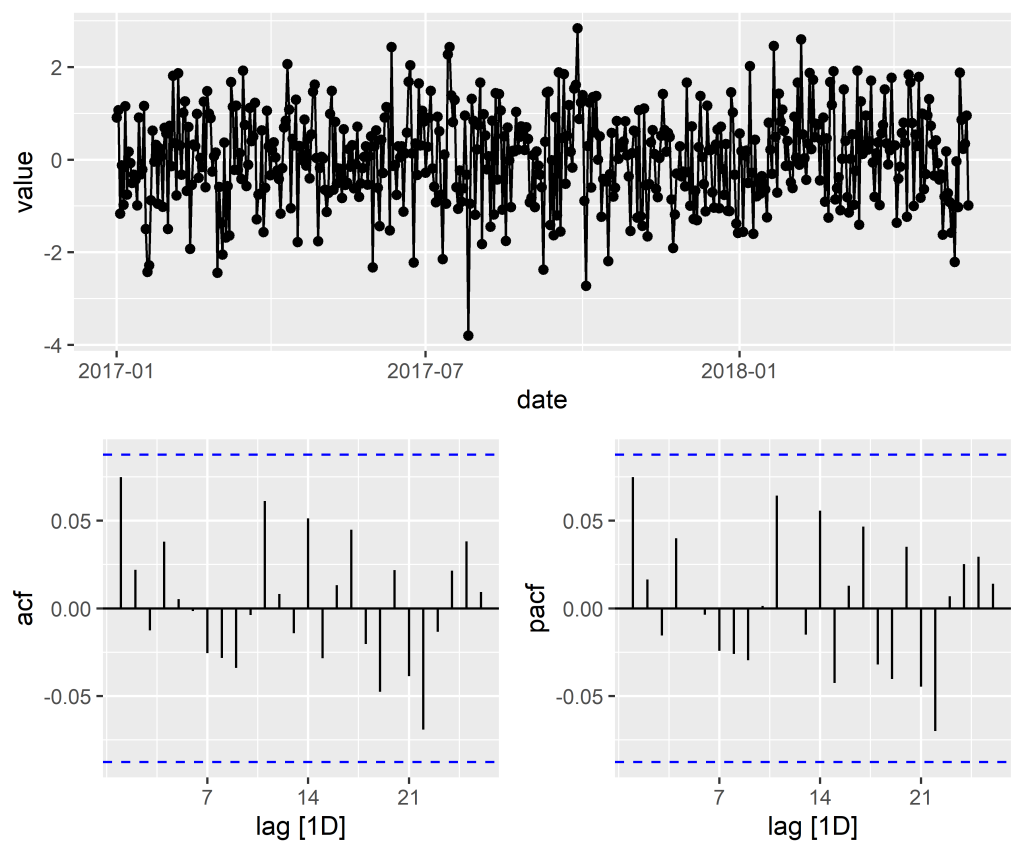
A partir da construção dessa função, em termos gráficos, nós podemos obter informações úteis sobre a natureza do processo em questão, verificando o grau de associação entre as defasagens do mesmo. Da definição, observa-se que .} Para ilustrar no R, considere os retornos simples mensais da ação da Amazon, entre janeiro de 2014 e dezembro de 2018. O código abaixo ilustra o gráfico da série, a função de autocorrelação e função de autocorrelação parcial.
Modelos autorregressivos
Conforme vimos anteriormente, suponha que tenhamos um processo como
(11)
Onde . Como vimos, a trajetória desse processo depende de
. Se
, os choques se acumulam ao longo do tempo, formando assim um processo não estacionário. Por enquanto, entretanto, vamos considerar o caso em que
, de modo que tenhamos um processo estacionário. Assim, aplicando o operador defasagem à equação acima, temos que: O operador defasagem é definido como
. Ver sobre \href{https://en.wikipedia.org/wiki/Lag_operator}{aqui}.
(12)
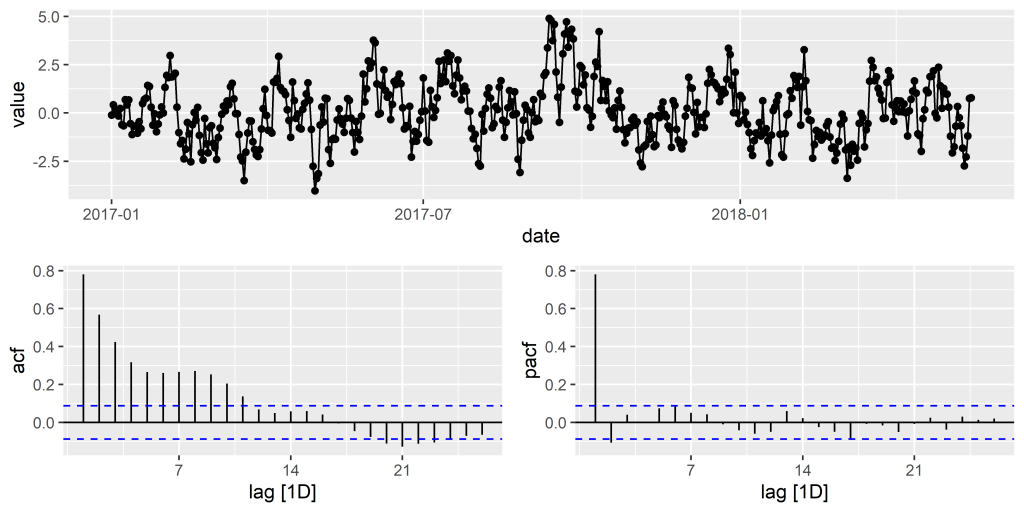
O processo descrito pela equação anterior é conhecido na literatura como processo autoregressivo de primeira ordem, bastante útil na modelagem e previsão de séries onde a primeira defasagem possui significância estatística. Para ilustrá-lo, vejamos as séries abaixo:
Um processo autorregressivo de primeira ordem, por seu turno, pode ser generalizado para um AR(p) da forma abaixo:
(13)
Processos de Médias Móveis
Mostramos na seção anterior como inverter um processo AR(1) para um processo de média móvel entre choques contemporâneos e passados. Vamos considerar agora, com base em @pfaff, justamente esse tipo de processo. Como fizemos antes, vamos começar por um processo MA(1) como abaixo:
(14)
onde é um ruído branco e
e
podem ser quaisquer constantes. Os momentos do MA(1) podem ser expressos como
(15)
Observe que nem a média, nem a autocovariância são dependentes do tempo, logo é possível estabelecer que o MA(1) é covariância estacionário para todos os valores de . Assim como fizemos com o AR(1), podemos gerar um processo MA(1). Abaixo simulamos um MA(1) com
.
Analogamente ao AR(1), também podemos generalizar um MA(1) para um MA(q) como abaixo:
(16)
Processos ARMA(p, q)
Agora que temos uma noção do que são processos autoregressivos e de média móveis, podemos juntar os dois. Desta forma podemos analisar processos mistos, ou processos ARMA. Este processo, ARMA(p,q), mais geral pode ser formulado como a seguir
(17)
Abaixo, vemos as funções de autocorrelação e autocorrelação parcial de um processo simulado ARMA(1,1):
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas

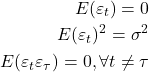
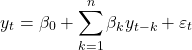
![Rendered by QuickLaTeX.com \begin{align*} \mu& = E(y_{t}) = E(\mu + \varepsilon_{t} + \theta\varepsilon_{t-1}) \\ \gamma_{0}& = E(y_{t} - \mu)^2 = (1 + \theta^2)\sigma^2 \\ \gamma_{1}& = E\left [(y_{t} - \mu)(y_{t-1} - \mu) \right ] = \theta\sigma^2 \end{align*}](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-5ed3f72892ecbe90ab1decd259db4caf_l3.png)