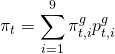Gerando Previsões Combinadas para a Inflação a partir dos grupos do IPCA

A inflação cheia medida pelo IPCA em um período $t$ qualquer nada mais é do que a soma da contribuição da inflação em cada um dos seus nove grupos, de acordo com os pesos dos mesmos no índice. Em outros termos,

(1) $\begin{align*} \pi_t = \sum_{i=1}^{9} \pi_{t,i}^{g} p_{t,i}^{g} \end{align*}$

onde $\pi_t$ é a inflação cheia, $\pi_{t,i}^{g}$ é a inflação em $t$ no grupo $i$ e $p_{t,i}^{g}$ é o peso em $t$ do grupo $i$ no índice cheio. De modo a ilustrar, podemos baixar com o pacote sidrar, as variações e os pesos desses nove grupos do IPCA, conforme o código abaixo.


## Pacotes
library(sidrar)
library(ggplot2)
library(forecast)
library(timetk)
library(zoo)
library(scales)
library(tidyverse)

## Baixar e tratar os dados
tab1 = get_sidra(api='/t/2938/n1/all/v/63,66/p/all/c315/7170,7445,7486,7558,7625,7660,7712,7766,7786/d/v63%202,v66%204')
tab2 = get_sidra(api='/t/1419/n1/all/v/63,66/p/all/c315/7170,7445,7486,7558,7625,7660,7712,7766,7786/d/v63%202,v66%204')
tab3 = get_sidra(api='/t/7060/n1/all/v/63,66/p/all/c315/7170,7445,7486,7558,7625,7660,7712,7766,7786/d/v63%202,v66%204')

series = c(7170, 7445, 7486, 7558, 7625, 7660,
7712, 7766, 7786)

names = c('Alimentos', 'Habitação', 'Art de Resid',
'Vestuário', 'Transporte', 'Saúde e cuid pessoais',
'Despesas Pessoas', 'Educação', 'Comunicação')

var1 <- matrix(NA, ncol=length(series),
nrow=nrow(tab1)/length(series)/2)

peso1 <- matrix(NA, ncol=length(series),
nrow=nrow(tab1)/length(series)/2)

var2 <- matrix(NA, ncol=length(series),
nrow=nrow(tab2)/length(series)/2)

peso2 <- matrix(NA, ncol=length(series),
nrow=nrow(tab2)/length(series)/2)

var3 <- matrix(NA, ncol=length(series),
nrow=nrow(tab3)/length(series)/2)

peso3 <- matrix(NA, ncol=length(series),
nrow=nrow(tab3)/length(series)/2)

for(i in 1:length(series)){

var1[,i] <- tab1`Variável (Código)`==63&
tab1Valor[tab2`Geral, grupo, subgrupo, item e subitem (Código)`==series[i]]

var3[,i] <- tab3`Variável (Código)`==63&
tab3Valor[tab1`Geral, grupo, subgrupo, item e subitem (Código)`==series[i]]

peso2[,i] <- tab2`Variável (Código)`==66&
tab2Valor[tab3`Geral, grupo, subgrupo, item e subitem (Código)`==series[i]]
}

variacao = ts(rbind(var1, var2, var3), start=c(2006,07), freq=12)
peso = ts(rbind(peso1, peso2, peso3), start=c(2006,07), freq=12)

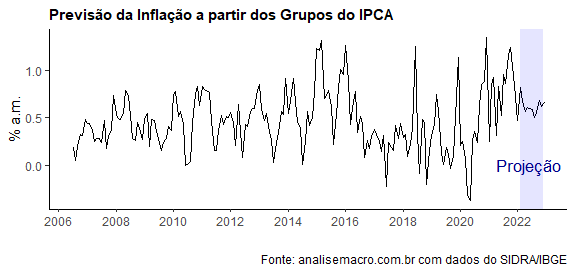
Assim, a inflação medida pelo IPCA nada mais será do que a variação vezes o respectivo peso do grupo. Com isso em mente, nós podemos gerar a previsão para cada grupo e depois recuperar a previsão da inflação cheia a partir dessas previsões individuais. O resultado é exposto no gráfico abaixo.

A previsão para a inflação em janeiro, por essa metodologia, é de 0,47%.

________________

(*) Para aprender a fazer esse tipo de projeção, veja nossos cursos de Previsão Macroeconométrica e Modelos Preditivos aplicados à Macroeconomia.

(**) Os códigos completos do exercício estão disponíveis no Clube AM.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

O que são Agentes de IA?

As diferentes formas de avaliar o erro de um modelo de previsão

Previsão do CPI usando text mining

Nowcasting do PIB usando a linguagem R

Previsão de demanda com o Prophet usando Python

Nowcasting do PIB: um modelo de fatores usando Python

Outros artigos relacionados

O que são Agentes de IA?

O que é um agente e como ele funciona? Como agentes tomam decisões usando racioncínio e planejamento? Neste artigo, nosso objetivo é investigar estas questões para construir um conhecimento fundamental sobre AI agents.

As diferentes formas de avaliar o erro de um modelo de previsão

Existem tantas siglas para métricas de desempenho de modelos preditivos que é fácil se perder na sopa de letrinhas. Neste artigo, fornecemos uma visão geral das principais métricas para avaliar e comparar modelos de regressão e classificação, usando exemplos com dados em Python.

Previsão do CPI usando text mining

Exploramos neste exercício, de forma similar a Ferreira (2022), a utilidade de tópicos latentes extraídos dos comunicados do FOMC, por um modelo LDA, na previsão da inflação norte-americana, medida pelo CPI. O objetivo é comparar um modelo econométrico simples, tal como um AR-GAP de Faust e Wright (2013), em especificações com e sem os fatores textuais.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!