Introdução a dados financeiros e suas características

O objetivo da Econometria Financeira é prover conhecimentos básicos sobre séries temporais financeiras, introduzir técnicas estatísticas úteis para analisar dados financeiros, bem como apresentar aplicações práticas de alguns métodos econométricos. Nesse post, nós vamos discutir alguns conceitos básicos sobre como coletar dados financeiros, bem como algumas formas avaliar as propriedades estatísticas dessas séries.

Para obter todo o código do processo de criação dos gráficos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

Dados do mercado acionário brasileiro

Dados de ações

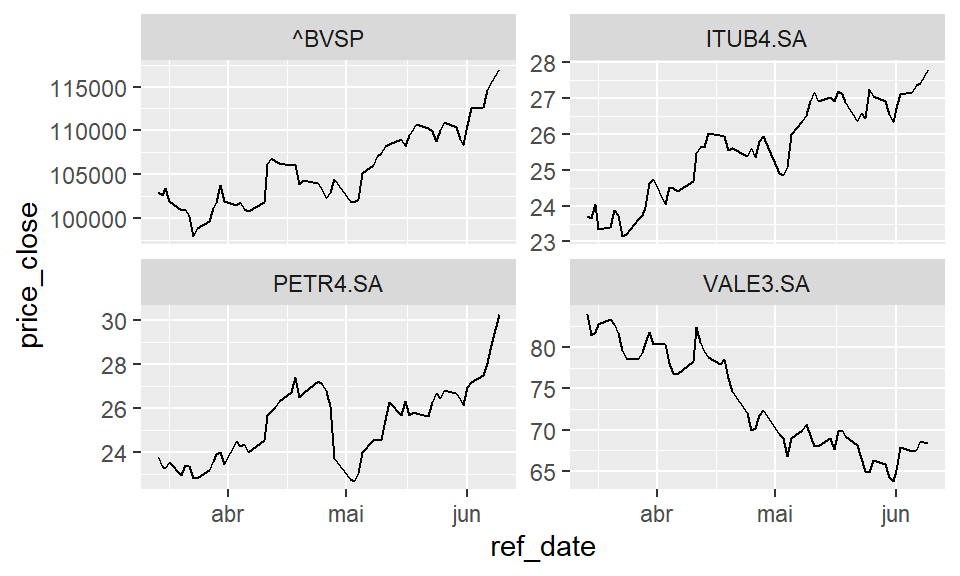
Para ter acesso aos dados da B3, isto é, preços de ações no geral, nós podemos fazer uso do pacote `yfR`. Tal pacote permite acessar dados diretamente da API do site do Yahoo Finance. Um exemplo é posto abaixo.

Dados da curva de juros

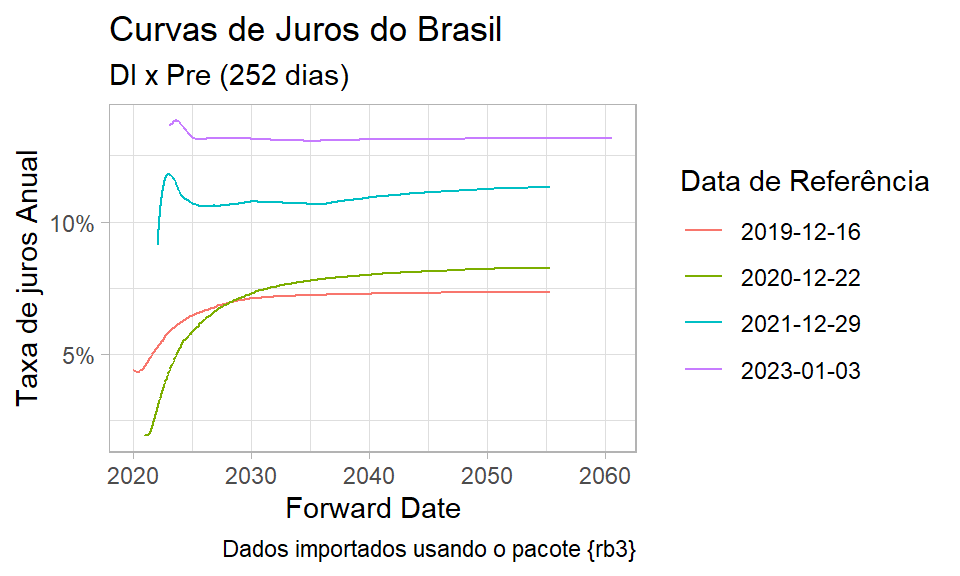
Diversos dados da B3 podem ser acessados via o pacote `rb3`. Com facilidade, extraímos os dados referentes a curvas de juros da B3.

Dados do Tesouro Direto

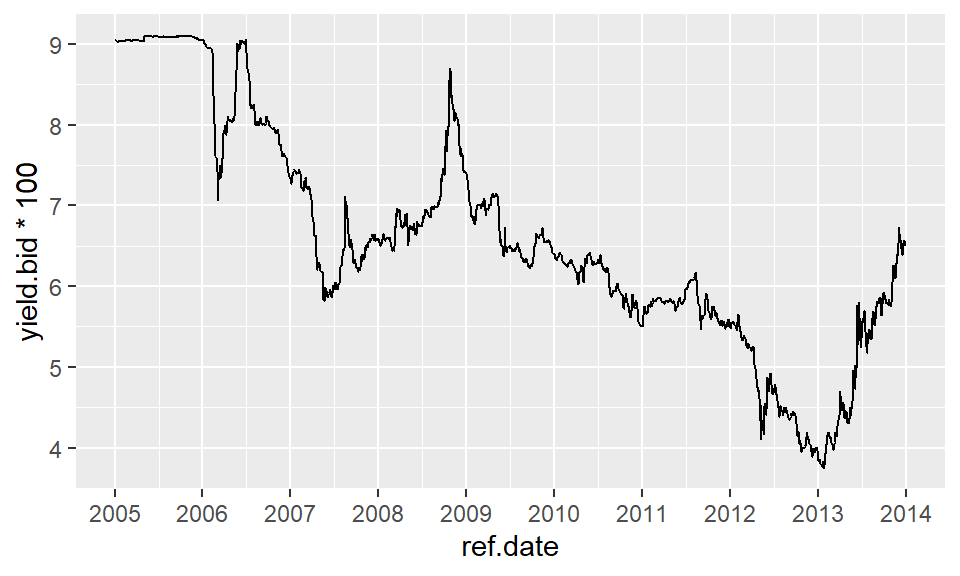
É possível também obter dados do Tesouro Direto fazendo uso do pacote `GetTDData`. Abaixo, um exemplo.

Propriedades de Séries Financeiras

Retorno de Ativos

Uma grande parte dos estudos financeiros envolve retorno, ao invés de preço, de ativos. Isto porque, retorno de ativos pode ser um completo sumário para oportunidades de investimento, bem como séries de retorno são mais fáceis de lidar do que séries de preço porque aquelas possuem propriedades estatísticas mais atrativas.

Há, entretanto, diversas definições de retorno de ativos. Para mostrar algumas, tome $P_t$ como o preço de um ativo no tempo $t$ , bem como considere a princípio que o ativo não paga dividendos.

Retorno simples de um período

Ao manter um ativo por um período de $t-1$ a $t$ , isso resultaria em um retorno bruto simples de

(1) $\begin{align*} 1 + R_t = \frac{P_t}{P_{t-1}} \end{align*}$

O retorno líquido ou simples então será de

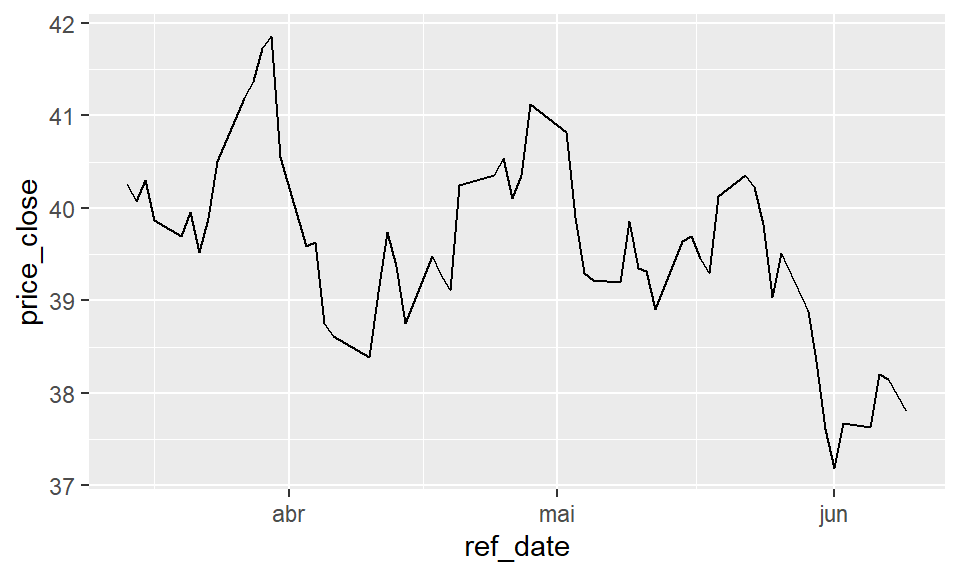
(2) $\begin{align*} R_t = \frac{P_t}{P_{t-1}} - 1 = \frac{P_t - P_{t-1}}{P_{t-1}} \end{align*}$

Para demonstrar, considere as ações da WEGE3 como abaixo.

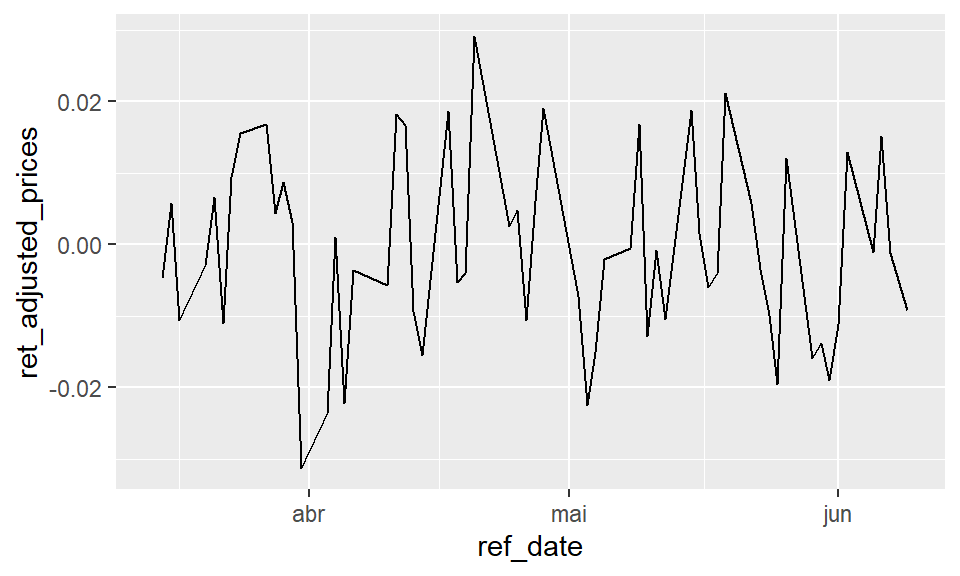
Podemos calcular facilmente os retornos simples diários do preço da ação acima. Como resultado obtemos a série demonstrada no gráfico abaixo.

Retorno simples de vários períodos

Ao manter um ativo por $k$ período entre $t-k$ e $t$ gera um retorno simples bruto de

(3) $\begin{align*} 1 + R_t[k] =& \frac{P_t}{P_{t-k}} = \frac{P_t}{P_{t-1}} \times \frac{P_{t-1}}{P_{t-2}} \times ... \times \frac{P_{t-k+1}}{P_{t-k}} \nonumber \\ =& (1 + R_t)(1 + R_{t-1}) ... (1 + R_{t-k+1}) \nonumber \\ =& \prod_{j=0}^{k-1} (1 + R_{t-j}) \nonumber \end{align*}$

Assim, o retorno simples de k-períodos será simplesmente o produto dos k retornos simples de um período envolvidos. Isto é chamado de retorno composto. O retorno líquido simples de k-períodos será então $R_t[k] = (P_t - P_{t-k})/P_{t-k}$ .

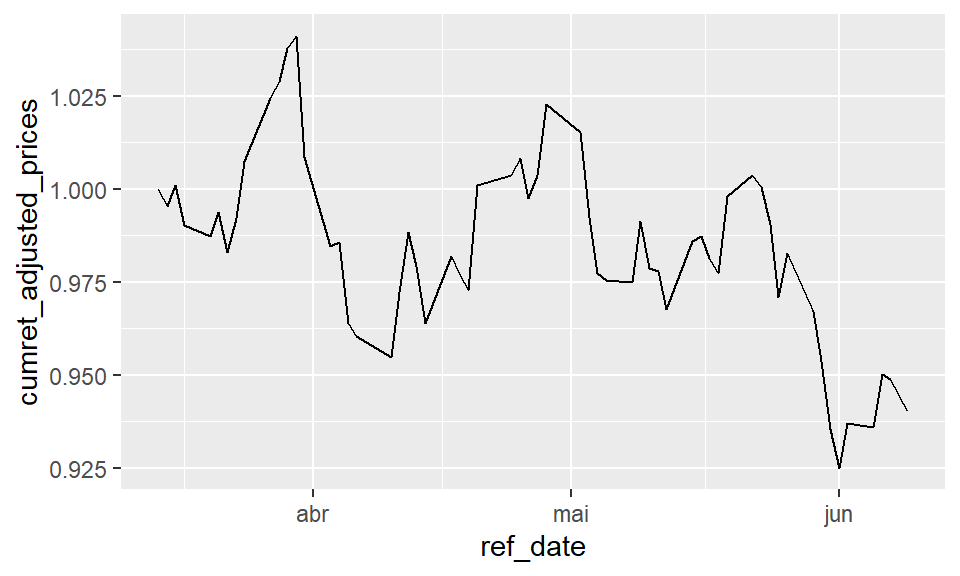
Podemos capturar facilmente o retorno de vários períodos, calculados diariamente, resultando no gráfico abaixo.

Retorno Anualizado

Na prática, o intervalo de tempo real é importante para discutir e comparar retornos - por exemplo, retorno mensal ou anual. Se o intervalo de tempo não é dado, é assumido implicitamente um ano. Se o ativo for mantido por $k$ anos, então o retorno médio anualizado é definido como

(4) $\begin{align*} \text{Anualizado} \left \{ R_t[k] \right \} = \begin{bmatrix} \prod_{j=0}^{k-1} (1 + R_{t-j}) \end{bmatrix}^{\frac{1}{k}} - 1 \end{align*}$

Isso é a média geométrica dos $k$ retornos brutos simples de um período envolvidos e que pode ser calculado como

(5) $\begin{align*} \text{Anualizado} \left \{ R_t[k] \right \} = \text{exp}\begin{bmatrix} \frac{1}{k} \sum_{j=0}^{k-1} \text{ln} (1 + R_{t-j}) \end{bmatrix} - 1 \end{align*}$

onde exp(x) é a função exponencial e ln(x) é o logaritmo natural do número positivo x. Porque é mais fácil calcular médias aritméticas do que médias geométricas e porque o retorno de um período tende a ser pequeno, às vezes é possível utilizar uma expansão de Taylor de primeira ordem para aproximar o retorno anualizado, de modo que

(6) $\begin{align*} \text{Anualizado} \left \{ R_t[k] \right \} \approx \frac{1}{k} \sum_{j=0}^{k-1} R_{t-j} \end{align*}$

Composição contínua

Antes de apresentar o retorno composto continuamente, vamos discutir o efeito de combinar. Assuma, por exemplo, que a taxa de juros de um depósito seja de 10% ao ano e que o depósito inicial seja de $ 1. Se o banco paga juros uma vez por ano, então o valor líquido do depósito se torna $ $1(1+0.1)$ = $ 1,1, um ano depois. Se o banco paga juros de seis em seis meses, a taxa passa a ser de 5% e o valor líquido será então de R$ $1(1+0.1/2)^2$ = $ 1.1025, depois do primeiro ano. Em geral, se o banco paga juros m vezes por ano, então a taxa de juros para cada pagamento será de $10\%/m$ e o valor líquido do depósito se torna $ $1(1 + 0.1/m)^m$ , um ano depois. O valor líquido de $ 1.1052, que é obtido por exp(0.1) é conhecido como resultado de composição contínua.

De modo geral, o valor líquido do ativo A de uma composição contínua será

(7) $\begin{align*} A =& C \, \text{exp} (r \times n) \end{align*}$

onde $r$ é a taxa de juros ao ano, $C$ é o capital inicial e $n$ é o número de anos. Da equação acima, nós temos que

(8) $\begin{align*} C =& A \, \text{exp} (-r \times n) \end{align*}$

que nada mais é do que o valor presente de um ativo que vale $A$ reais $n$ anos a partir de hoje, assumindo que a taxa de juros composta continuamente é $r$ ao ano.

Retorno composto continuamente

O logaritmo natural do retorno bruto simples de um ativo é chamado de retorno composto continuamente ou log retorno:

(9) $\begin{align*} r_t = \text{ln} (1+R_t) = \text{ln} \frac{P_t}{P_{t-1}} = p_t - p_{t-1} \end{align*}$

onde $p_t = \text{ln} (P_t)$ . $r_t$ possui algumas vantagens sobre o retorno líquido $R_t$ . Primeiro, considere retornos de multiperíodos. Nós temos

(10) $\begin{align*} r_t[k] =& \text{ln} (1+R_t[k]) = \text{ln}[(1+R_t)(1 + R_{t-1}) ... (1+R_{t-k+1})] \nonumber \\ =& \text{ln} (1+R_t) + \text{ln} (1+R_{t-1}) + ... + \text{ln} (1+ R_{t-k+1}) \nonumber \\ =& r_t + r_{t-1} + ... + r_{t-k+1} \nonumber \end{align*}$

portanto, o retorno multiperíodo composto continuamente é simplesmente a suma dos retornos de um período compostos continuamente envolvidos. Segundo, as propriedades estatísticas do log retornos são mais tratáveis.

Retorno de carteira de investimentos

O retorno líquido simples de um portfólio contendo $N$ ativos é a média ponderada dos retornos líquidos simples dos ativos envolvidos. Onde o peso de cada ativo é a porcentagem do valor investido no portfólio daquele ativo. Chame de $p$ o portfólio que põe peso $w_i$ para o ativo $i$ . Assim, o retorno simples de $p$ no período $t$ será $R_{p,t} = \sum_{i=1}^{N} w_i R_{it}$ , onde $R_{it}$ é o retorno simples do ativo $i$ .

O retorno composto continuamente de um portfólio, entretanto, não possui a propriedade conveniente acima. Se os retorno simples $R_{it}$ são todos pequenos em magnitude, então nós temos $r_{p,t} \approx \sum_{i=1}^{N} w_i r_{it}$ , onde $r_{p,t}$ é o retorno composto continuamente de um portfólio no período $t$ .

Pagamento de Dividendos

Se um ativo paga dividendos periodicamente, nós precisamos modificar a definição de retorno de um ativo. Chame de $D_t$ o pagamento de dividendos de um ativo entre $t-1$ e $t$ , e $P_t$ o preço do ativo ao final do período $t$ . Assim, os dividendos não estão incluídos em $P_t$ . Então, o retorno líquido simples e composto continuamente no tempo $t$ se torna

(11) $\begin{align*} R_t = \frac{P_t + D_t}{P_{t-1}} - 1, \quad r_t = ln(P_t + D_t) - ln(P_{t-1}) \nonumber \end{align*}$

Retorno em excesso

Retorno em excesso de um ativo no tempo $t$ é a diferença entre o retorno do ativo e o retorno de algum ativo de referência. O ativo de referência é em geral aquele livre de risco, como algum título público. O retorno em excesso simples e seu log retorno podem ser expressos como

(12) $\begin{align*} Z_t = R_t - R_{0t}, \quad z_t = r_t - r_{0t} \end{align*}$

onde $R_{0t}$ e $r_{0t}$ são o retorno simples e log retorno do ativo de referência.

Sumário

A relação entre retorno simples $R_t$ e o log retorno (ou composto continuamente) $r_t$ é

(13) $\begin{align*} r_t = ln(1+R_t), \quad R_t = e^{r_t} - 1 \nonumber \end{align*}$

se o retorno $R_t$ e $r_t$ estão em porcentagens, então

(14) $\begin{align*} r_t = 100 ln(1+ \frac{R_t}{100}), \quad R_t = 100 (e^{rt/100} - 1) \nonumber \end{align*}$

A agregação temporal dos retornos produz

(15) $\begin{align*} 1 + R_t[k] = (1+R_t)(1+R_{t-1})...(1+R_{t-k+1}) \nonumber \\ r_t[k] = r_t + r_{t-1} + ... + r_{t-k+1} \nonumber \end{align*}$

Se a taxa de juros composta continuamente é $r$ ao ano, então a relação entre valor presente e valor futuro de um ativo será

(16) $\begin{align*} A = C \, exp(r \times n), \quad C = A \, exp(-r \times n) \nonumber \end{align*}$

Bond yields e preços

Bonds são instrumentos financeiros que pagarão o valor de face para quem os mantiver durante o tempo de maturação. Alguns bonds também pagam juros periodicamente na forma de cupom. Zero-cupom bonds, por suposto, não pagam juros periodicamente. Bond yield, por seu turno, é o retorno que um investidor irá receber por ter mantido o bond durante a maturação. Obs. Bond em uma tradução livre seria uma obrigação.

Rendimento atual

O rendimento atual (current yield) refere-se ao retorno percentual que o pagamento anual do cupom provê ao investidor. Matematicamente, nós temos

(17) $\begin{align*} \text{Rendimento atual} = \frac{\text{Pagamento de juros}}{\text{Preço de Mercado}} \times 100\% \nonumber \end{align*}$

Para zero-cupom bonds, o rendimento atual é calculado como

(18) $\begin{align*} \text{Rendimento atual} = \begin{pmatrix} \frac{\text{Valor de Face}}{\text{Preço de Compra}} \end{pmatrix}^{1/k} - 1 \nonumber \end{align*}$

Rendimento até o vencimento

o rendimento atual não considera o valor do dinheiro no tempo, porque ele não considera o valor presente do pagamento de cupons que o investidor irá receber no futuro. Por isso, a forma mais comum de cálculo é o rendimento até o vencimento (\emph{yield to maturity}). Para calcular o YTM, considere a soma a valor presente do valores futuros, isto é,

(19) $\begin{align*} P = \frac{C_1}{1+y} + \frac{C_2}{(1+y)^2} + ... + \frac{C_k + F}{(1+y)^k} \end{align*}$

onde $F$ representa o valor de face e $C_i$ é o fluxo de caixa de pagamentos de cupons.

Volatilidade implícita

Stock options são contratos financeiros. Uma call option na ação A dá ao seu proprietário o direito, mas não obrigatório, de comprar certa parte da ação A a um preço pré-estabelecido em um dado período de tempo. Uma put option, por outro lado, dá a seu detentor o direito, mas não obrigatório, de vender certa quantidade da ação a um preço pré-estabelecido em um dado período de tempo. Esse preço é chamado de strike price e o tempo é referido como time to maturity.

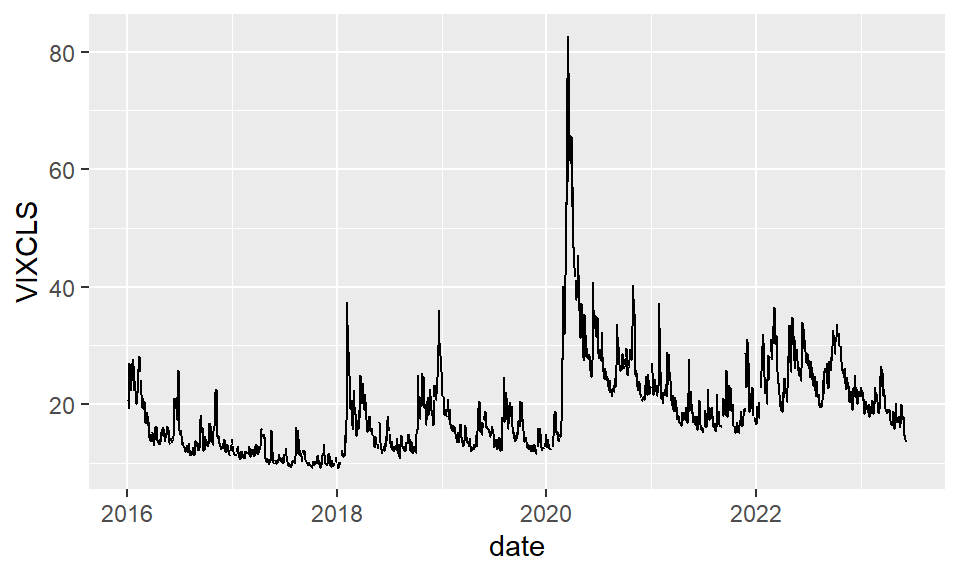
O preço de uma opção depende de muitos fatores tal qual o strike price, taxa de juros livre de risco, o preço atual e a volatilidade da ação. Em particular, a volatilidade de ações é chamada de volatilidade implícita e serve como um dos termômetros para os investidores. O mais famoso é calculado pelo CBOE, Índice de Volatilidade (VIX). É atualmente baseado no S&P 500, estimando a volatilidade esperada por meio da média dos preços ponderados do SPX, puts e calls sobre uma ampla variedade de strike prices. No R podemos utilizar novamente o pacote quantmod para visualizá-lo.

_____________________

Quer saber mais?

Veja nossa trilha de cursos de Finanças Quantitativas

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise do Censo Demográfico com o R

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Criando um Dashboard de análise de Ações no Python

Analisando séries temporais no Python e esquecendo de vez o Excel

Cálculo do Retorno Econômico de uma Política Pública

Outros artigos relacionados

Análise do Censo Demográfico com o R

Como podemos analisar dados do Censo Demográfico para produzir pesquisas e implementar políticas públicas? Mostramos nesta postagem o resultado de uma breve análise dos dados preliminares do Censo Demográfico de 2022 usando o R.

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Colocar modelos em produção pode ser um grande desafio. Lidar com custos monetários, infraestrutura operacional e complexidades de códigos e ferramentas pode acabar matando potenciais projetos. Uma solução que elimina todos estes obstáculos é a recém lançada Shinylive. Neste artigo mostramos um exemplo com um modelo de previsão para o preço do petróleo Brent.

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Manter relatórios diários com dados e análises atualizados é um desafio, pois envolve várias etapas: coleta de dados, tratamento de informações, produção de análises e atualização de relatório. Para superar este desafio algumas ferramentas como Python + Quarto + GitHub podem ser usadas para automatizar tudo que for automatizável. Neste artigo mostramos um exemplo com dados do mercado financeiro.