A validação cruzada é uma técnica que utiliza algoritmos iterativos para avaliar a capacidade de generalização de modelos em ciência de dados. O principal objetivo de uso da técnica é avaliar a acurácia de um modelo preditivo, antes do mesmo ser utilizado para dados desconhecidos.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
Durante o desenvolvimento de modelos preditivos, os dados observados são usualmente separados em duas amostras:
- Uma amostra de treinamento, utilizada pelo modelo para estimar parâmetros;
- Outra amostra de teste, utilizada pelo modelo para produzir previsões.
O objetivo da separação de amostras é verificar o desempenho do modelo para dados desconhecidos. Trata-se de um esquema de previsão pseudo fora da amostra, onde a amostra de teste cumpre este papel de dados desconhecidos, na tentativa de reproduzir o que aconteceria na prática se o modelo fosse utilizado em uma aplicação. Dessa forma, é possível detectar e evitar problemas como sobreajuste, sub-ajuste ou viés de seleção.
A técnica de validação cruzada se diferencia da simples separação de amostras de treino/teste ao aplicar este procedimento diversas vezes. Uma única separação de amostras pode introduzir viés na avaliação de modelos, problema este que pode ser evitado utilizando a validação cruzada. Ao final, obtém-se uma visão geral sobre o desempenho do modelo para diversos dados de treino/teste, avaliando a acurácia média de múltiplas iterações.
Pré-requisitos para ler este artigo
Antes de continuar, certifique-se de que os tópicos listados a seguir não são de outro mundo para você:
- Você entende como a reamostragem de dados funciona.
- Você entende como as estruturas de repetição em linguagens de programação funcionam.
Caso necessite, confira os cursos de Programação para Análise de Dados e de Modelagem e Previsão para aprender mais sobre estes assuntos.
Motivação
Imagine o seguinte cenário. Você quer prever a taxa de inflação nos próximos 12 meses. Após coletar, processar e investigar os dados, você separou o último ano de observações para a amostra de teste e treinou um super modelo de machine learning usando a amostra de treino. Com as previsões do modelo para a amostra de teste, você conseguiu calcular que o modelo erra, em média, 0.0004 a variação mensal da inflação. Uau! Motivo para festejar, não?
A pergunta fundamental a ser feita ao avaliar um modelo preditivo é: como saber se os resultados de acurácia se generalizam? O desempenho de um modelo avaliado ao separar os dados uma única vez em treino/teste fornece pouca informação sobre a sua generalização. Com uma nova amostra de teste, os resultados podem ser completamente diferentes. Até mesmo com uma amostra diferente de treino, os parâmetros e, portanto, as previsões podem ser diferentes.
A validação cruzada é uma técnica para mensurar o erro de modelos preditivos de forma “agnóstica” aos dados. A ideia é obter uma medida de erro que sumarize o desempenho do modelo se o mesmo fosse aplicado para diferentes amostras, possivelmente com características pontuais distintas. Dessa forma, modelos que são muito bons com uma ou poucas amostras, podem não possuir o mesmo desempenho em uma avaliação mais ampla.
Em termos formais, o objetivo de uso da técnica de validação cruzada é encontrar a acurácia média de modelos preditivos usando k amostras. Em um problema clássico de regressão, onde a variável resposta é numérica, esse erro poderia ser mensurado de várias formas. Em geral, a métrica mais simples pode ser definida como o erro médio de validação cruzada:
Onde são os valores observados da variável alvo de previsão,
são os valores previstos pelo modelo e
é amostra de teste de validação cruzada, definida por alguma técnica (a seguir).
Vantagens e desvantagens da validação cruzada
Os principais pontos fortes da validação cruzada são:
- Permite avaliar a capacidade de generalização de um modelo preditivo;
- É flexível para diferentes objetivos e estruturas de dados;
- É simples de utilizar e interpretar.
Os principais pontos fracos da validação cruzada são:
- Variáveis não estacionárias e transformações nos dados podem dificultar ou introduzir viés;
- Costuma exigir grandes quantidades de dados;
- Pode ser intensivo computacionalmente.
Agora vamos entender como definir as amostras k de validação cruzada para avaliar modelos preditivos.
Validação cruzada para dados ordenados
As técnicas de validação cruzada para dados ordenados são utilizadas para definir k amostras respeitando uma sequência ou índice dos dados. O caso mais comum de aplicação são as séries temporais, que são estruturas de dados que possuem ordenamento temporal.
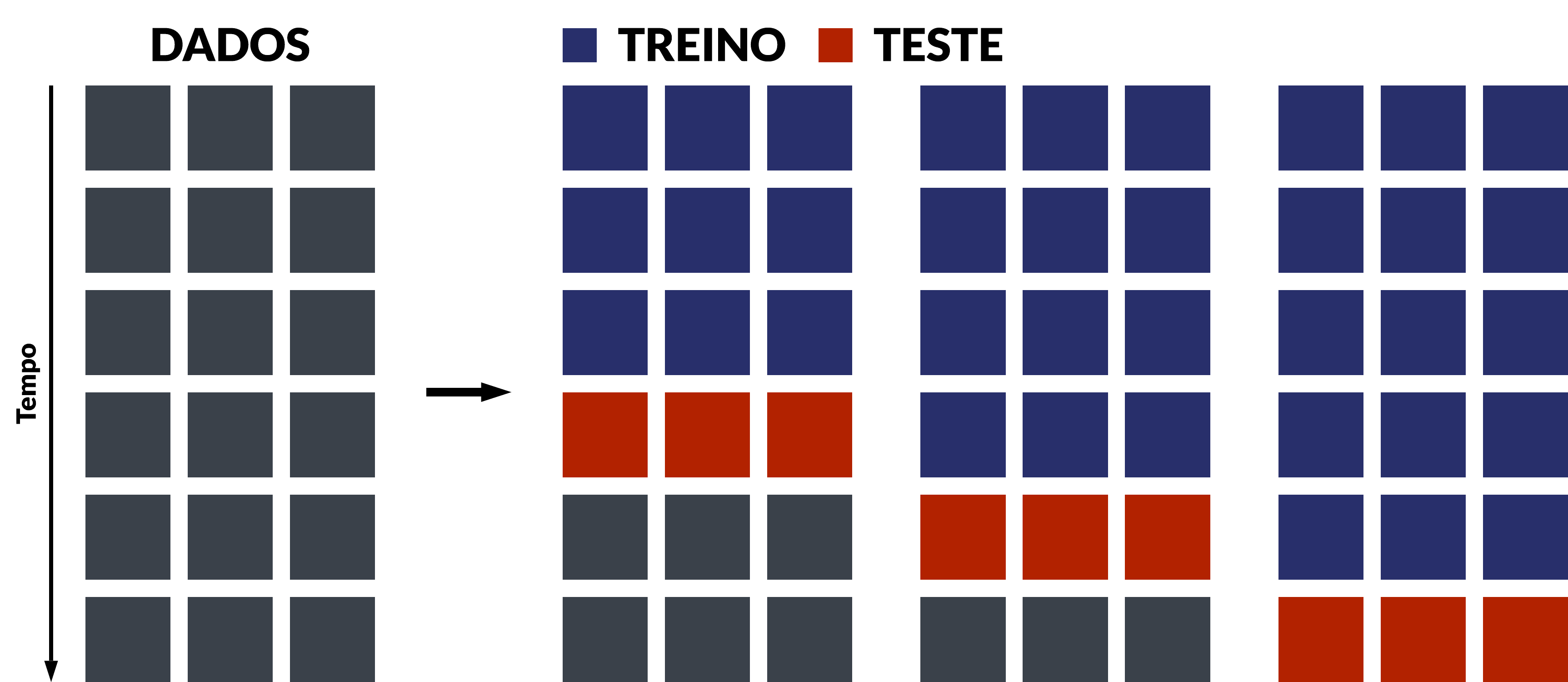
A validação cruzada com janela expansiva é a técnica mais comumente utilizada quando os dados são ordenados, como no caso das séries temporais. A imagem abaixo ilustra como esta técnica funciona:
A operacionalização da técnica pode ser resumida nestas etapas:
- Defina o tamanho inicial da amostra de treino a partir do conjunto de dados completo;
- Defina o tamanho fixo h da amostra de teste, correspondente ao horizonte de previsão;
- Separe k subamostras de treino, acrescentando um ou j períodos iterativamente, até o total de períodos menos h;
- Estime o modelo para cada k amostra de treino;
- Produza previsões h passos à frente, utilizando os k modelos da etapa anterior;
- Calcule o erro de previsão para cada k amostra;
- Calcule a média dos erros de previsão ou métrica de interesse.
Este esquema de validação cruzada é simples e flexível. Se o objetivo é encontrar um modelo que produza boas previsões ℎ=6 passos à frente, então não faz sentido produzir previsões um passo à frente. Se a quantidade de dados é grande, a cada iteração podem ser acrescentados j períodos na amostra de treino. E por fim, cada amostra de treino de validação cruzada pode ser fixa também. Se fizer sentido treinar o modelo com 30 observações, basta fixar essa quantidade no algoritmo acima.
Validação cruzada para dados não ordenados
As técnicas de validação cruzada para dados não ordenados são utilizadas para definir k amostras sem considerar qualquer índice ou sequência dos dados. O caso mais comum de aplicação são os dados de corte transversal, que são estruturas de dados que são coletados em apenas um período no tempo.
Existem várias técnicas de validação cruzada para dados não ordenados. Algumas técnicas são aplicáveis quando o conjunto de dados é pequeno, já outras podem ser a única opção viável quando o conjunto é grande. A seguir abordamos a principal das técnicas, explorando o seu funcionamento e métricas derivadas.
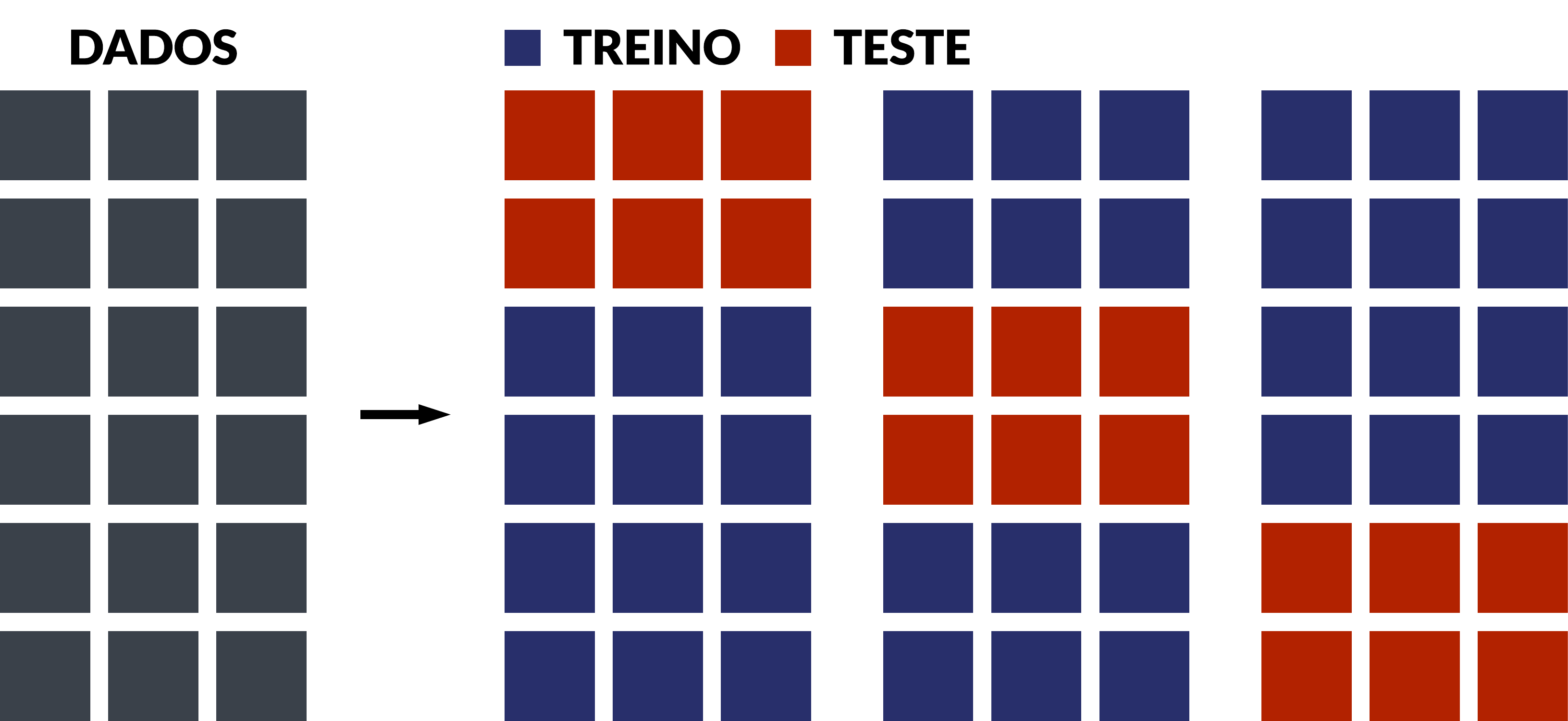
Validação cruzada de k dobras (k-fold CV)
A operacionalização da técnica pode ser resumida nestas etapas:
- Defina um número k de dobras (ou grupos) para particionar o conjunto de dados completo;
- Particione aleatoriamente o conjunto de dados completo em k dobras de igual tamanho;
- Escolha uma dobra para deixar de fora do modelo (amostra de teste);
- Estime o modelo com as k-1 dobras restantes (amostra de treino);
- Calcule o erro de previsão para cada k dobra;
- Repita as etapas 4 e 5 k vezes, deixando de fora uma dobra (etapa 3) diferente cada vez;
- Calcule a média dos erros de previsão ou métrica de interesse.
A vantagem desta técnica é que todas as observações no conjunto de dados são usadas para treino e para teste, sendo que cada observação é usada para teste apenas uma vez. A imagem abaixo ilustra como esta técnica funciona, tomando como exemplo k=3:
Exemplo aplicado com dados
Agora vamos praticar com código as duas técnicas de validação cruzada expostas acima usando modelos preditivos.
Validação cruzada para dados ordenados
Vamos fazer um exemplo com séries temporais usando um modelo simples. O código abaixo implementa a técnica com janela expansiva usando 180 como tamanho da janela inicial, acrescentando 1 observação sucessivamente e usando 12 como horizonte de previsão:
0.49377276989155294Note que o RMSE de validação cruzada é maior do que o encontrado em outro exercício mais simples.
Validação cruzada para dados não ordenados
Vamos fazer um exemplo com dados de corte transversal usando um modelo simples. O código abaixo implementa a técnica de validação cruzada de k dobras usando 10 como número de dobras:
76985.63638026986Note que o RMSE de validação cruzada é maior do que o encontrado em outro exercício mais simples.
Conclusão
Como saber se o desempenho de um modelo preditivo se generaliza para dados desconhecidos? Dividir a tabela de dados em duas amostras, treinar o modelo e calcular o erro é um processo comum e bastante simples, mas pouco informativo. As técnicas de validação cruzada podem ajudar neste aspecto e neste artigo mostramos como funcionam e como implementar usando linguagem de programação.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
Referências
G. James, D. Witten, T. Hastie, and R. Tibshirani. An Introduction to Statistical Learning with applications in R. Springer, 2017.
R. Hyndman and G. Athanasopoulos. Forecasting principles and practice. 1rd edition. OTexts, 2019.

![Rendered by QuickLaTeX.com \[EM_{VC} = \frac{1}{k} \sum^{k}_{i=1} (y_i - \hat{y_i})\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-00ddfa6dc7da68a06c635a621334d722_l3.png)